概要
直流機の回転数\(N[rpm]\)、トルク\(T[N・m]\)は、磁極数、電機子導体数や、電機子巻線の接続方法といった内部構造によって大きく異なります。
本頁では、直流機のトルク\(T[N・m]\)について、重要要素を踏まえた電流とトルクの関係式の導出を行います。
トルク\(T[N・m]\)
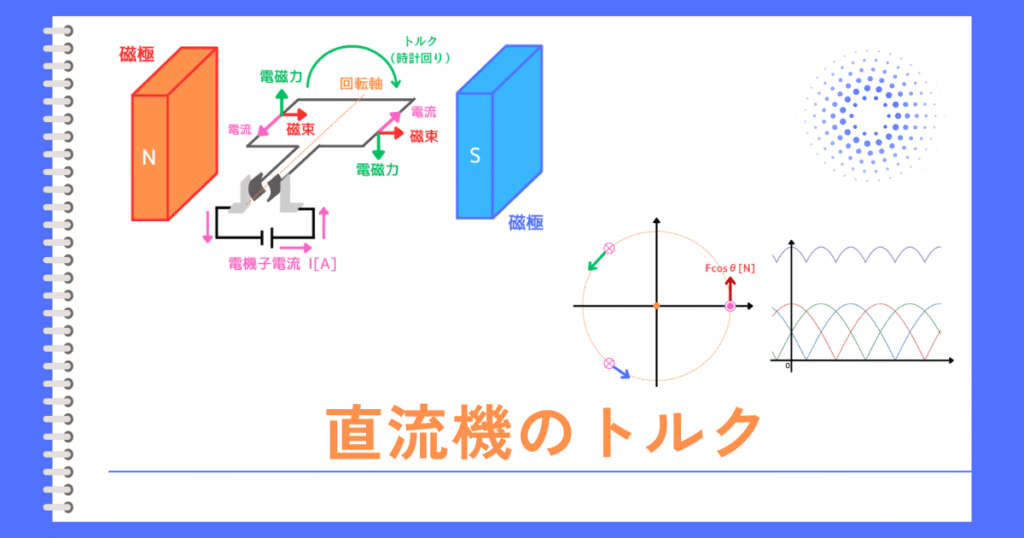
トルクとは
トルクは、回転軸を中心にして、回転子を回転させる力のことです。
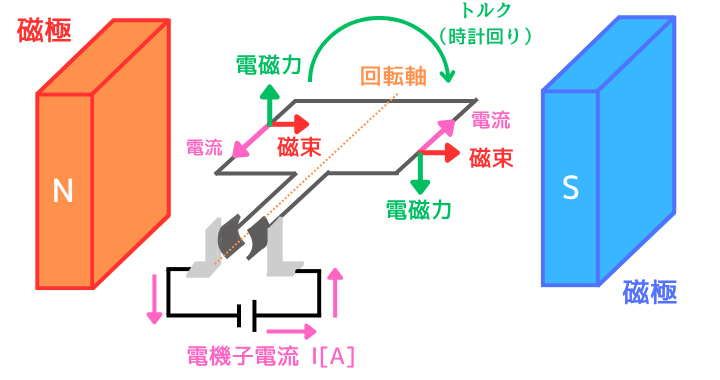
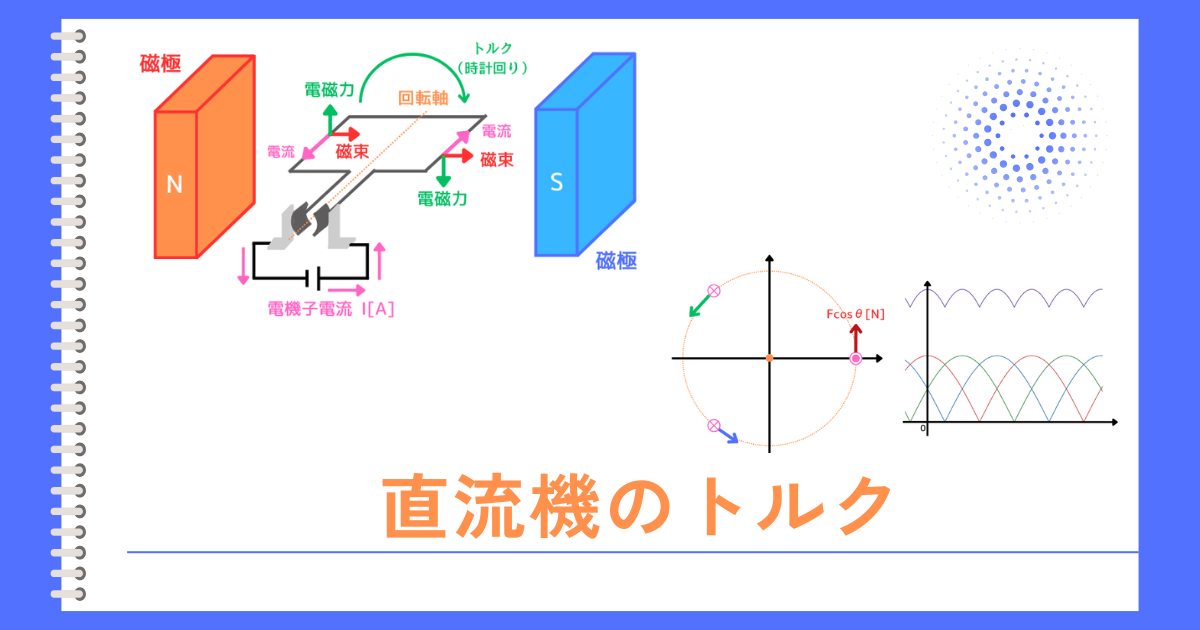
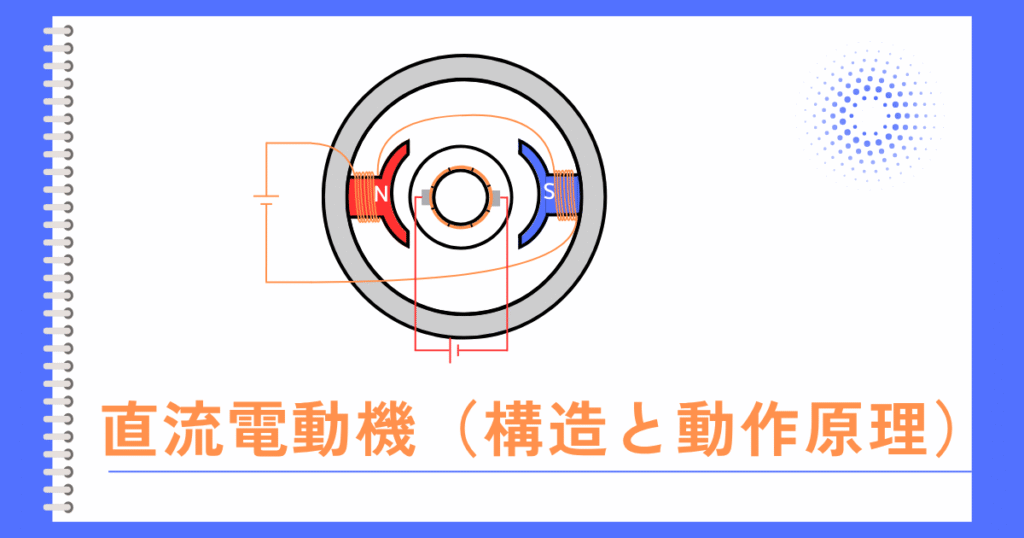
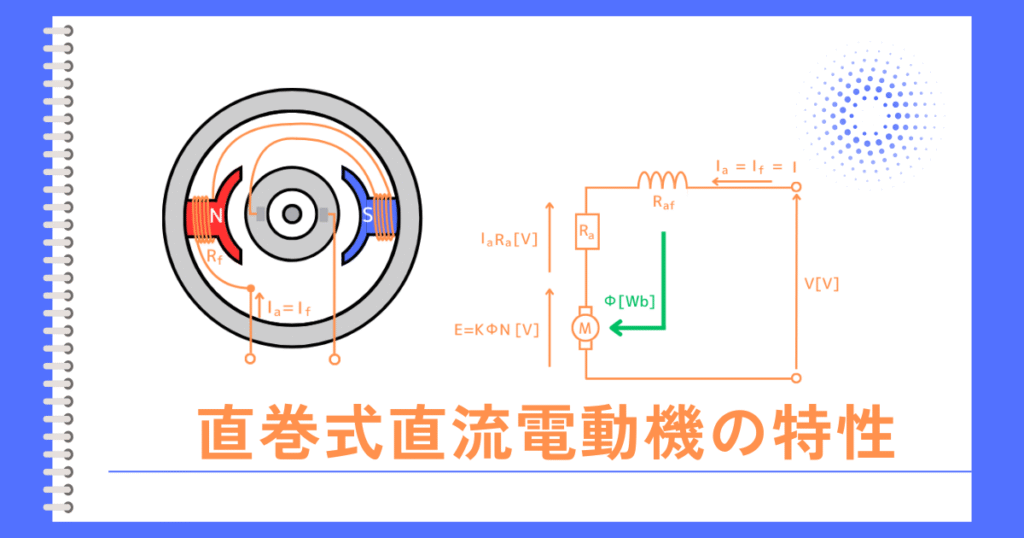
左図のように向かい合わせたN・Sの磁石を磁極と呼びます。この磁極から磁束を供給する仕組みを界磁と呼びます。
磁極の間に電機子巻線のコイルに電源を接続することで、電機子電流\(I[A]\)が流れます。
電機子電流が、界磁の磁束を横切ることで、フレミング左手の法則で示される方向に、ローレンツ力(電磁力)が発生します。
このローレンツ力によって、回転軸を中心に、電機子巻線のコイルが回転します。
このコイルを回転させる力がトルクとなります。
重要公式
界磁Φ[Wb]で、回転数N[rpm]で回転している直流発電機の出力電圧E[V]の関係式
\(\displaystyle \boldsymbol{T=\frac{pZ}{2πa}・\Phi・I}\)
上記関係式の機械的な要素を比例定数\(K_T\)にまとめた場合、
\(\boldsymbol{T=K_T・\Phi・I}\)
※直流機の運転に関する問題で確実に使用する最も重要な式です。
\(\displaystyle \boldsymbol{T=\frac{pZ}{2πa}・\Phi・I}\)の式からわかること
・磁極数\(p\)が増加すると、トルク\(T\)が増加する。
・1回路の導体数\(\frac{Z}{a}\)が大きい波巻だと、小電流でトルクが大きくなる。
トルクの式の簡単な導出
トルクT[N・m]、機械出力P[W]と、角速度ω[rad/s]の関係式を変形します。
\(P=Tω\)
⇔ \(\displaystyle T=\frac{P}{ω}\) …①
回転子の角速度\(ω[rad/s]\)を回転数\(N[rpm]\)で表すと、
\(\displaystyle ω=2π・\frac{N}{60}\) …②
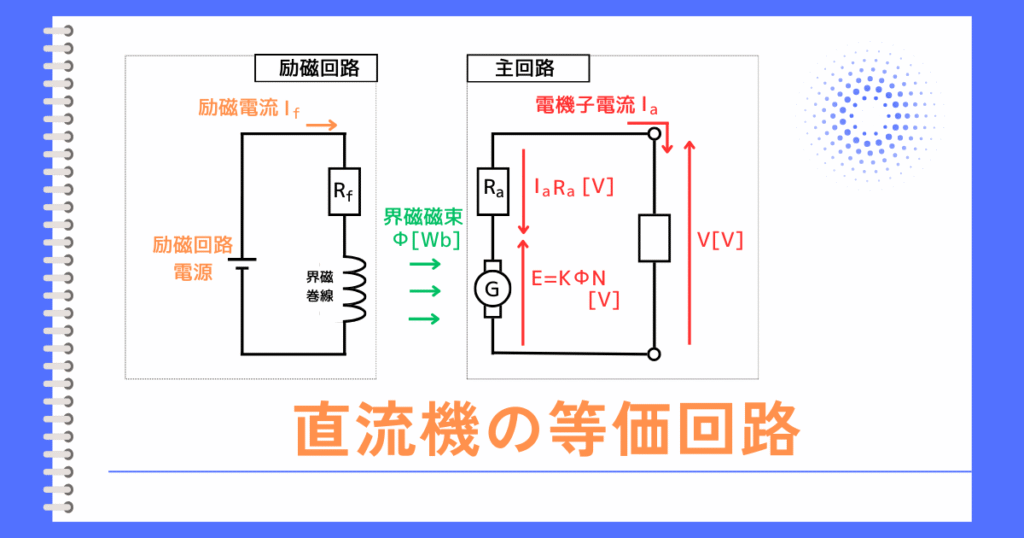
機械出力\(P[W]\)と、消費電力\(W[W]\)は等しいです。
そのため、電機子電圧\(E[V]\)、電機子電流\(I[A]\)とすると、
\(P=W=E・I\) …③
⇧のリンクのページで導出した電機子電圧\(E\)と、回転数\(N[rpm]\)の式から、
\(\displaystyle E=\frac{pZ}{60a}・\Phi・N\) …④
③式に④式を代入すると、
\(\displaystyle P=E・I=\frac{pZ}{60a}・\Phi・N・I\) …⑤
①式に②・⑤式を代入すると、
\(\displaystyle T=\frac{P}{ω}=\frac{\frac{pZ}{60a}・\Phi・N・I}{2π・\frac{N}{60}}=\frac{pZ}{2πa}・\Phi・I\)
➡ \(\displaystyle T=\frac{pZ}{2πa}・\Phi・I\) …⑥
ここで、トルクに関する比例定数を\(K_T\)とし、
\(\displaystyle K_T=\frac{pZ}{2πa}\)
とすると、⑥式は次のように簡単化できます。
\(T=K_T・\Phi・I\) …⑦
トルクの式をローレンツ力から導出
重要公式で示した式について、直流電動機として、式を組み立てて導出します。
導出の工程は長いため、(1)~(5)の5工程に分けて示します。
(1)ローレンツ力の式

ローレンツ力\(F[N]\)の大きさは、
・界磁磁束の磁束密度\(B[Wb/m^2]\)
・電機子電流\(I[A]\)
・電機子導体の長さ\(L[m]\)
としたとき、
\(F=BIL[N]\) …①
です。
(2)電機子導体に流れる電流の導出
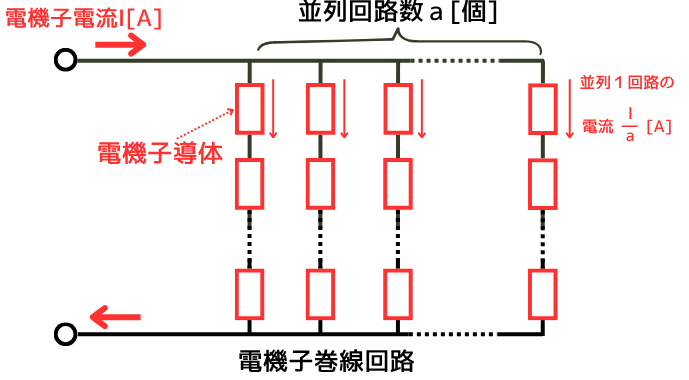
整流子・ブラシから見た電機子巻線を、回路図として展開した電機子巻線回路です。
ローレンツ力が働く電機子導体が、直列につながれた回路を、さらに並列に並べて電機子巻線が構成されています。
・並列回路数:\(a\)[個]
・電機子電流:\(I[A]\)
とすると、
並列1回路に流れる電流\(\frac{I}{a}[A]\) …②
(3)界磁の磁束密度の導出
・磁束密度の導出
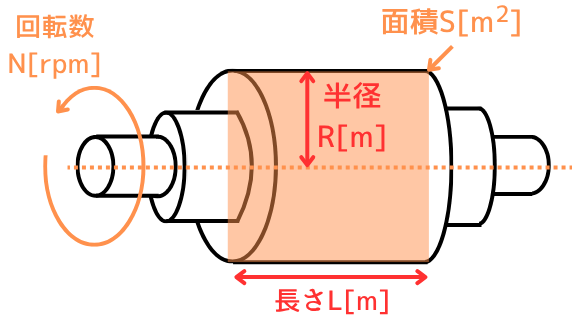
電機子巻線のコイル内を貫く界磁磁束の磁束密度\(B[Wb/m^2]\)は、磁束\(\Phi[Wb]\)を面積\(S[m^2]\)で割った値です。
\(B=\frac{\Phi}{S}[Wb/m^2]\) …③
回転子の半径を\(R[m]\)、回転子の長さを\(L[m]\)としたとき、回転子の断面積\(S[m^2]\)は、
\(S=2RL[m^2]\) …④
③式に④式を代入すると、
\(\displaystyle B=\frac{\Phi}{2RL}[Wb/m^2]\) …⑤
・磁極数の考慮
ここで、\(\Phi\)は、1極当たりの磁束です。
磁極数に応じて、磁束が変化するので、具体例を3つ程上げます。(例よりも多い磁極数の直流機もあります)
\(p=2\)極の場合は、N・S極が1組で、電機子巻線を1回横切るので、磁束は\(\Phi\)です。
\(p=4\)極の場合は、N・S極が2組で、電機子巻線を2回横切るので、磁束は\(2 \Phi\)です。
\(p=6\)極の場合は、N・S極が3組で、電機子巻線を3回横切るので、磁束は\(3 \Phi\)です。
上記の関係から、磁極数\(p\)によって、磁束\(\Phi\)は\(\frac{p}{2}\)倍となります。
⑤式を磁極数を考慮して式を書き直すと、
\(\displaystyle B=\frac{p \Phi}{4RL}\) …⑥
となります。
(4)ローレンツ力のまとめ
ローレンツ力の式である①式に、②・⑥式を代入すると、
\(\displaystyle F=BIL=\frac{p}{4aR}・\Phi・I\) …⑦
となります。
この⑦式は、電機子導体1本にかかるローレンツ力です。
次に、全電機子導体が作り出す回転方向の力(トルク)を考えていきます。
(5)トルクの導出
・電機子導体1本のトルク式の導出
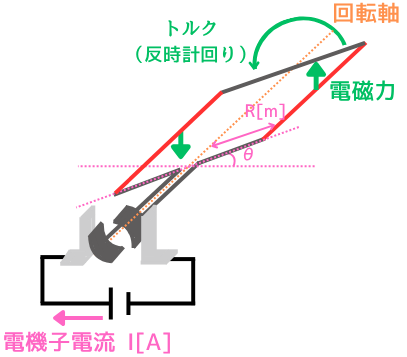
(左)角\(θ[rad]\)回った時点の図
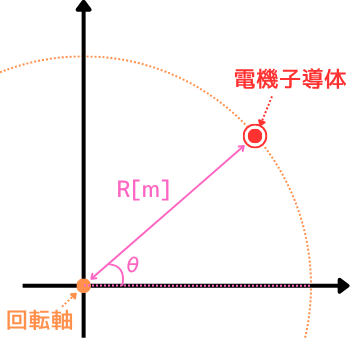
(右)回転軸(ブラシ側)から見た時の位置関係
上図(左)は、電機子導体が平行だった時を\(0[rad]\)として、\(θ[rad]\)回転したときの図です。
上図(右)は、回転子の回転軸側から電機子導体を見た時の位置関係です。
磁束密度\(B[Wb/m^2]\)に対してローレンツ力\(F[N]\)は常に垂直に働きます。
それに対し、回転力であるトルク\(T[N・m]\)は、円の接線方向に働く力によるモーメントです。
したがって、ローレンツ力\(F\)は、全てトルク\(T[N・m]\)に変換されるわけではありません。
では、ローレンツ力からトルクに変換していきます。
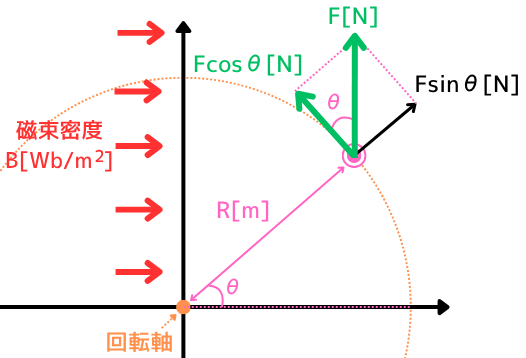
ローレンツ力\(F\)は、2つの方向の力に分解できます。
・接線方向:\(F_T=F・cosθ\)
・法線方向:\(F・sinθ\)
このうち、トルクに寄与するのは接線方向の力のみです。
トルク\(T[N・m]\)は、「回転方向の力\(F_T[N]\) × 回転軸からの距離\(R[m]\)」なので、次式で表されます。
\(T_1=F_T・R=F・cosθ・R\) …⑧
⑧式に⑦式を代入すると、
\(\displaystyle T_1=\frac{p}{4aR}・\Phi・I・cosθ・R=\frac{p \Phi I}{4a}cosθ\) …⑨
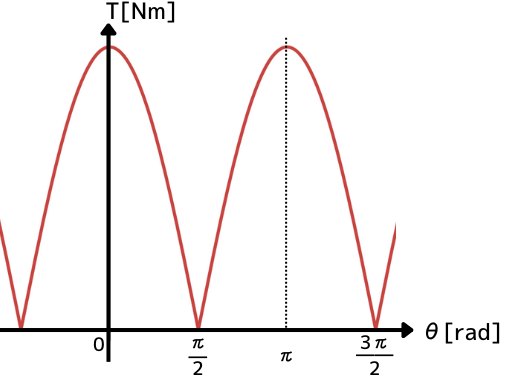
⑨式が、電機子導体1本にかかるトルク\(T_1\)であり、整流子によって電流の向きが切り替わることを考慮してグラフ化すると、左図のようになり、脈動していることがわかります。
- 電機子導体が磁束を垂直に横切る時(\(0[rad]\))
➡ トルクが最も大きくなります。 - 電機子導体が磁束と平行の時(\(\frac{π}{2}[rad]\))
➡ トルクは0になります。
・全体のトルクの導出
電機子導体1本だと、トルクが脈動するため、安定した回転力を得ることが出来ません。
しかし、導体の数を増やすことで、この点を改善することができます。
例として、電機子導体が3本の場合を考えてみます。
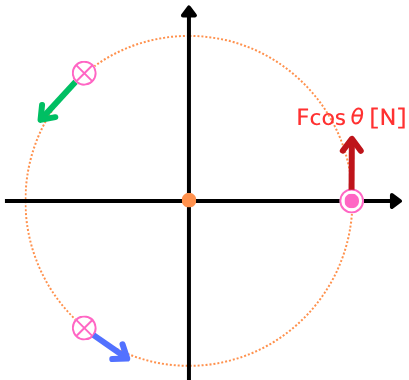
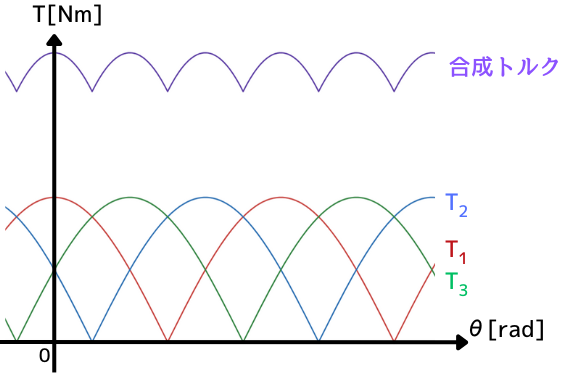
上図(左)のように、\(\frac{2π}{3}\)ずつの角度で3つの電機子導体が配置されているとします。
この時、上図(右)のようなグラフとなります。合成トルクは、3つの電機子導体のトルクを足し合わせた物となります。
電機子導体1本の時と比較して、脈動が小さくなっていることがわかります。
更に電機子導体の数を増やすことで、ほぼ一定な安定した合成トルクを得ることが出来ます。
合成トルクの大きさを計算します。
電機子導体の位置によって\(cosθ\)で変動する物を単純に足し合わせることは難しいので、トルクがほぼ一定で、脈動が無いものとして計算します。
この計算方法は、電機子導体1本のトルク\(T_1\) の平均値\(T_{1ave}\) を足し合わせることで、合成トルクを得ることが出来ます。
トルクの平均値\(T_{1ave}\)は、トルクのピーク値\(T_{1p}\)次の計算で求められ、
次の積分計算をすることで、平均値が、ピーク値の\(\frac{2}{π}\)倍であることがわかります。
\(\displaystyle T_{1ave}=\frac{1}{T}\int_0^T |T_{1p} cosθ|dθ=\frac{2}{π}T_{1p}\) …⑩
ここで、トルクのピーク値\(T_{1p}\)は⑨式の\(cosθ=1\)の時の値なので、
\(\displaystyle T_{1p}=\frac{p}{4aR}・\Phi・I・R=\frac{p \Phi I}{4a}\) …⑪
⑪式に⑩式を代入すると、トルクの平均値\(T_{1ave}\)は次のように表せます。
\(\displaystyle T_{1ave}=\frac{p \Phi I}{2πa}\) …⑫
⑫式から、電機子導体の総導体数\(Z\)本をかけることで、全体の合成トルク\(T[N・m]\)が求まります。
\(\displaystyle T=\frac{pZ}{2πa}・\Phi・I\) …⑬
ここで、\(\frac{pZ}{2πa}\)は、直流機の製作後は一切変化しない機械的な要素なので常に一定値です。
したがって、比例定数\(K_T\)に⑭式のようにまとめると、⑬式は⑮式のように簡潔に表記することができます。
\(\displaystyle K_T=\frac{pZ}{2πa}\) …⑭
\(T=K_T・\Phi・I\) …⑮
この式より、直流機のトルクは、運転中は磁束と電流に比例することがわかります。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
電験三種の領域をずっと超えた先の話を9割方しているので、電験三種の勉強の参考書としての購入はおすすめしません。
直流電動機について、ありとあらゆる事を書き記していった一冊です。
この本より詳しい本は少ないと思いますので、直流電動機の設計を学ぶ人に取っては良い本かと思われます。
感覚的には、研究論文化する内容ではないけど、後世には残しておきたいと思ったことをまとめたというような感じでしょうか。
文章の癖は強いので、もし買う場合はサンプルを読んでから購入することを推奨します。





コメント