概要
直流回路中のコイル、コンデンサの計算問題です。
定常状態の直流回路中ではコイルは短絡状態、コンデンサは開放状態として扱われることを理解している必要があります。順序だてて計算していく必要があるので、普通程度の難しさの問題です。
キーワード
定常状態、コイル、コンデンサ
問題
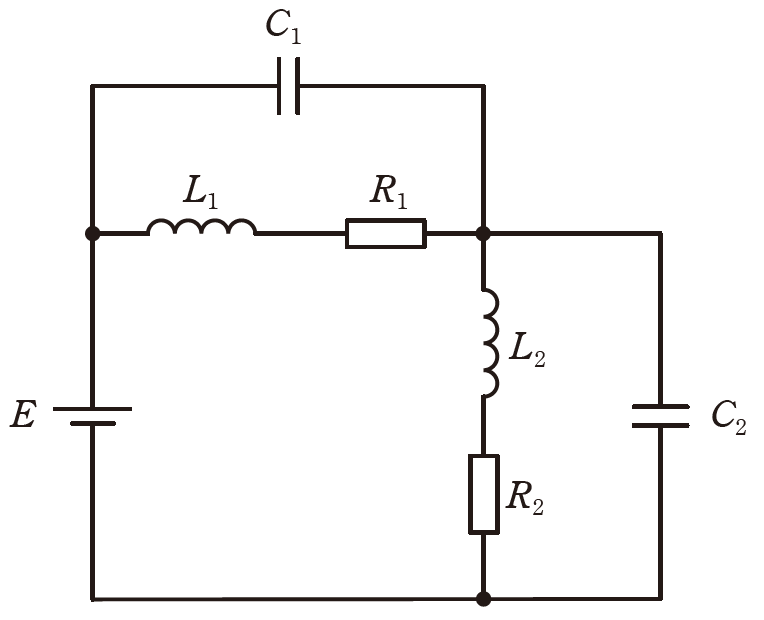
\(R_1=20Ω\)、\(R_2=30Ω\)の抵抗、インダクタンス\(L_1=20mH\)、\(L_2=40mH\)のコイル及び静電容量\(C_1=400μF\)、\(C_2=600μF\)のコンデンサからなる図のような直並列回路がある。
直流電圧\(E=100V\)を加えたとき、定常状態において\(L_1\)、\(L_2\)、\(C_1\)及び\(C_2\)に蓄えられるエネルギーの総和の値[J]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.12 (2) 1.20 (3) 1.32 (4) 1.40 (5) 1.52
答え
(5)
解説テキスト リンク
回答の解説
(1)直流回路中のコイルを短絡、コンデンサを開放処理して回路を描き直す
(2)回路全体に流れる電流と、各部分の電圧を求める
(3)2つのインダクタンスに蓄えられるエネルギーを求める
(4)2つのコンデンサに蓄えられるエネルギーを求める
(5)エネルギーの合計を求める
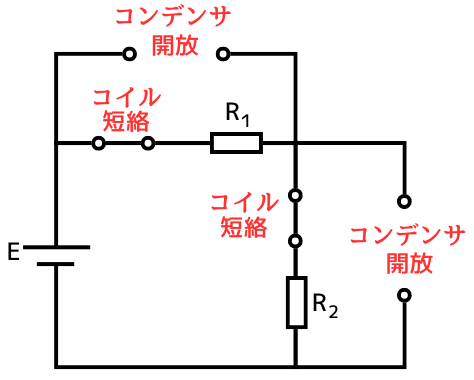
(1)直流回路中のコイルを短絡、コンデンサを開放処理して回路を描き直す
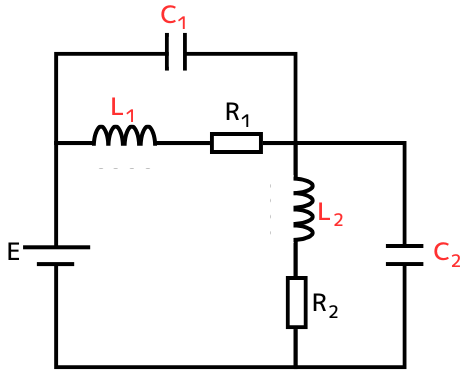
直流回路で定常状態のとき
・コイルも逆起電力を発生させないので、短絡されている状態と同じです。
・コンデンサには電流が流れないので、開放されている状態と同じです。
➡
(2)回路全体に流れる電流と、各部分の電圧を求める
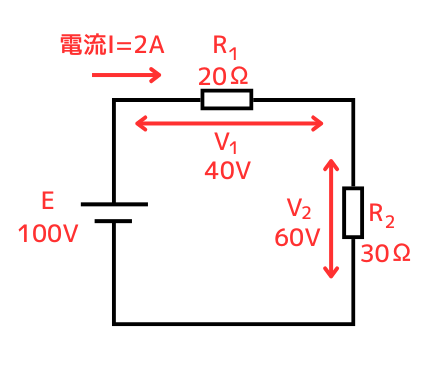
抵抗\(R_1\)、\(R_2\)が直列接続された回路と等価になります。
回路を描き変えると、左図のようになります。
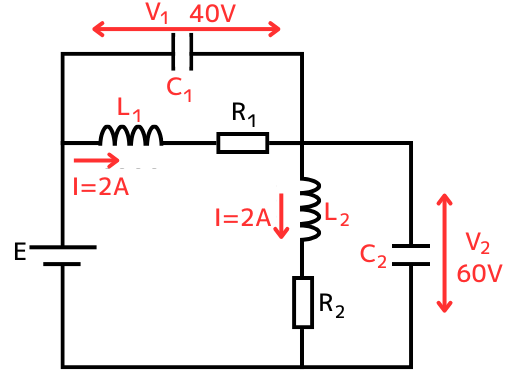
回路中に残った素子は、抵抗\(R_1=20Ω\)と\(R_2=30Ω\)のみです。\(E=100V\)の電源から、回路中に流れる電流\(I\)は、
\(\displaystyle I=\frac{E}{R_1+R_2}=2A\)
抵抗\(R_1\)の両端子間の電圧は、\(V_1=IR_1=40V\)
抵抗\(R_2\)の両端子間の電圧は、\(V_2=IR_2=60V\)
となります。
(3)2つのインダクタンスに蓄えられるエネルギーを求める
各電圧、電流がわかったので、次はコイル、コンデンサに蓄えられるエネルギーを求めていきます。
コイル\(L_1\)、\(L_2\)に蓄えられるエネルギー\(W_{L1}\)、\(W_{L2}\)は、
\(W_{L1}=\frac{1}{2}L_1I^2=\frac{1}{2}20×10^{-3}×2^2=0.04[J]\)
\(W_{L2}=\frac{1}{2}L_2I^2=\frac{1}{2}40×10^{-3}×2^2=0.08[J]\)
(4)2つのコンデンサに蓄えられるエネルギーを求める

コンデンサ\(C_1\)、\(C_2\)に蓄えられるエネルギー\(W_{C1}\)、\(W_{C2}\)は、
\(W_{C1}=\frac{1}{2}C_1V_1^2=\frac{1}{2}400×10^{-6}×40^2=0.32[J]\)
\(W_{C2}=\frac{1}{2}C_2V_2^2=\frac{1}{2}600×10^{-6}×60^2=1.08[J]\)
(5)エネルギーの合計を求める
エネルギーの合計\(W[J]\)は、
\(W=W_{L1}+W_{L2}+W_{C1}+W_{C2}=1.52[J]\)
以上より、答えは(5)1.52 です。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和6年度下期 第三種電気主任技術者試験 理論科目A問題問5
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント