概要
直流電動機、交流電動機のどちらに置いても、電動機出力は共通して
\(P=ωT\)
で表されます。
この式は、電動機を扱う上で最も重要な式です。
本ページでは、この式が、どのように導出されるかを示していきます。
公式
\(P=Tω\)
出力\(P[W]\)、トルク\(T[N・m]\)、角速度\(ω[rad/s]\)
\(ω=2π\frac{N}{60}\)
角速度\(ω[rad/s]\)、1分当たりの回転数\(N[min^{-1}\)
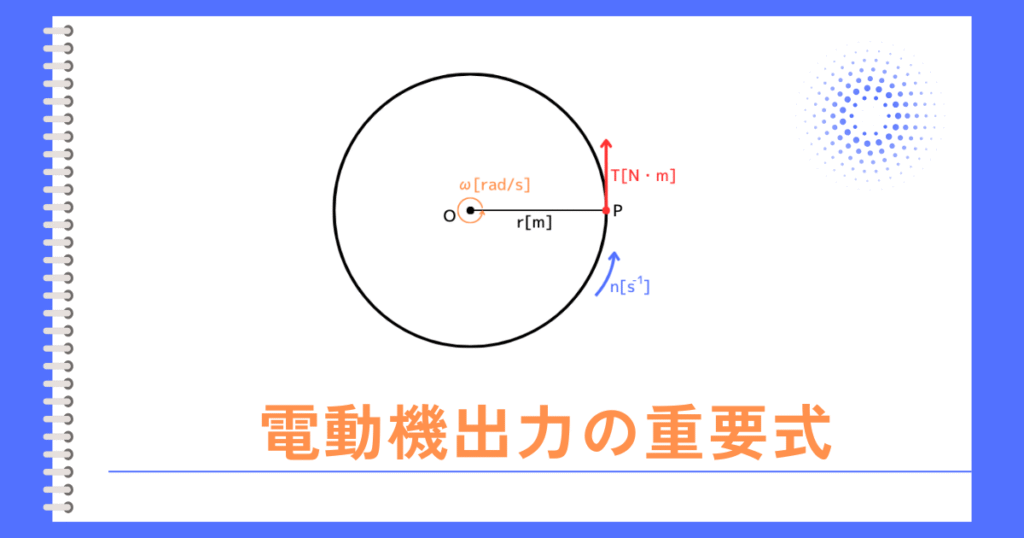
角速度\(ω[rad/s]\)
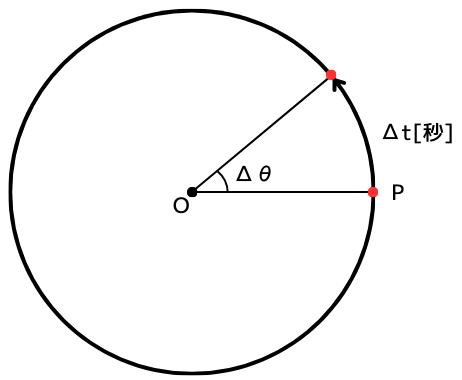
点Oの周りを回転している点Pが、
\(Δt\)秒の間に、\(Δθ[rad]\)だけ回転したとします。
この間の角度の変化率を角速度と呼び、
\(ω=\frac{Δθ}{Δt}\)
で表されます。
つまり、角速度は1秒当たりに回転する角度のことです。
角速度の単位[rad/s]
角速度の単位は[rad/s]で表されます。
[rad]は、弧度法と呼ばれる角度の表し方です。
[rad]は、ラジアンと読み、1回転したときに\(2π[rad]\)です。
[°]で表す度数法は、1回転したときに\(360[°]\)です。
計算で使う事が多い角度を、弧度法と度数法で表すと、次の通りです。
\(2π[rad]=360[°]\)
\(π[rad]=180[°]\)
\(\frac{π}{2}[rad]=90[°]\)
\(\frac{π}{3}[rad]=60[°]\)
\(\frac{π}{4}[rad]=45[°]\)
\(\frac{π}{6}[rad]=30[°]\)
回転数Nと角速度ω
電動機・発電機では、回転数\(N[min^{-1}]\)で表される事が大半です。
\(N[min^{-1}]\)は、1分間でN回、回転したことを表しています。
角速度\(ω[rad/s]\)は、1秒間で回転する角度なので、
1秒間の回転数\(n[sec^{-1}]\)としたとき、
\(ω=2πn[rad/s]\) …①
と表せます。
回転数\(N[min^{-1}]\)を、1秒当たりの回転数\(n[sec^{-1}]\)に変換すると、
1分は60秒なので、
\(n=\frac{N}{60}\) …②
①式に②式を代入すると、
\(ω=2π\frac{N}{60}[rad/s]\) …③
この③式は、電動機・発電機の回転数を扱う上で、最も重要な式とも言えるほど重要なので、式を暗記するのではなく、何故、このように表現されるかを理解しましょう。
出力\(P_o[W]\)
出力\(P_o[W]\)は、電気エネルギーから変換された、軸が回転する機械エネルギーです。
仕事量の概念から\(P_o=Tω\)を導出していきます。
(1)仕事量の復習
まず、仕事量\(W\)は、物体に力の大きさ\(F[N]\)を与え、力の方向に動いた距離が\(d[m]\)のときに、
\(W=Fd[N・m]\) …①
で表されます。
1秒間の仕事量を仕事率\(P[W]\)と呼びます。
\(W\)の仕事をするのにかかった時間\(t[s]\)で割ると、仕事率\(P[W]\)になります。
速度\(v=\)距離\(d÷\)時間\(t\)から、
\(P=\frac{W}{t}=\frac{Fd}{t}=Fv\) …②
出力\(P_o[W]\)は、単位からもわかる通り、仕事率であるため、②式で表された通り、
\(P_o=Fv\) …③
です。
(2)トルク\(T[N・m]\)
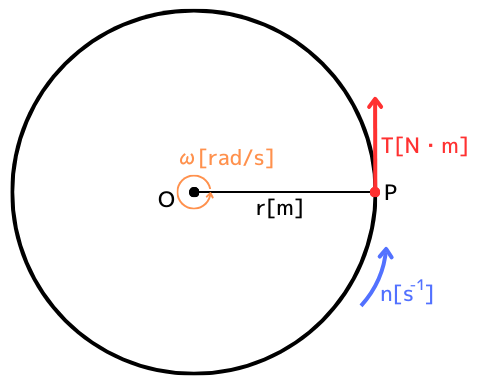
トルク\(T\)とは力のモーメントと呼ばれる、物体を回転させる力の働きを表す量のことです。
回転軸の中心点Oから、半径\(r[m]\)の円周に力\(F[N]\)が働くと、
\(T=Fr[N・m]\) …④
の回転させる力が働きます。
(3)回転体の移動距離\(d[m]\)
半径\(r[m]\)の回転体が一周したときの移動距離\(d[m]\)は、
\(d=2πr[m]\)
回転体がn回転した場合の移動距離\(d[m]\)は、
\(d=2πrn[m]\)
\(t=1\)秒間に\(d[m]\)の移動をしていたとすると、速度\(v[m/s]\)は、次のように求まります。
\(v=\frac{d}{t}=2πnr[m/s]\) …⑤
角速度\(ω[rad/s]\)は、1秒あたりに進む角度なので、次式で表されます。
\(ω=2πn[rad/s]\) …⑥
⑥式を⑤式に代入すると、
\(v=2πnr=ωr\) …⑦
(4)仕事率にトルクと速度を代入
仕事率(③式)にトルク(④式)、速度(⑦式)を代入すると、
\(P_o=Fv=\frac{T}{r}・ωr=ωT\)
➡\(P_o=ωT\) …⑧
以上で、出力\(P_o[W]\)が、角速度\(ω[rad/s]\)とトルク\(T[N・m]\)で表されることが示せました。
電験の問題等では、回転数\(N[min^{-1}]\)が与えられることが多いです。
角速度の解説で示したとおり、
\(ω=2π\frac{N}{60}\) …⑨
を、出力の式(⑧式)に代入すると、
\(P_o=2π\frac{N}{60}T\) …⑩
と表すことが出来ます。
出力\(P_o\)と、回転数\(N\)の値が与えられていて、トルク\(T\)を求める場合は、⑩式を変形させて、
\(T=\frac{P_o}{2π\frac{N}{60}}\) …⑪
と表すことが出来ます。
⑧式は、覚えておく必要がある式です。
⑩式や、⑪式は⑧式から簡単に導き出せる式なので、使う頻度はありますが、覚える価値はありません。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
電験三種の領域をずっと超えた先の話を9割方しているので、電験三種の勉強の参考書としての購入はおすすめしません。
直流電動機について、ありとあらゆる事を書き記していった一冊です。
この本より詳しい本は少ないと思いますので、直流電動機の設計を学ぶ人に取っては良い本かと思われます。
感覚的には、研究論文化する内容ではないけど、後世には残しておきたいと思ったことをまとめたというような感じでしょうか。
文章の癖は強いので、もし買う場合はサンプルを読んでから購入することを推奨します。






コメント