概要
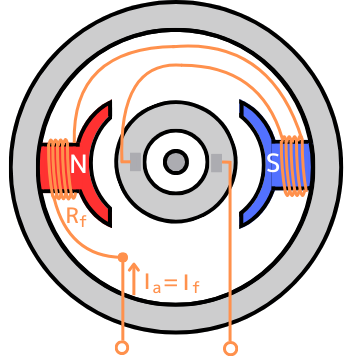
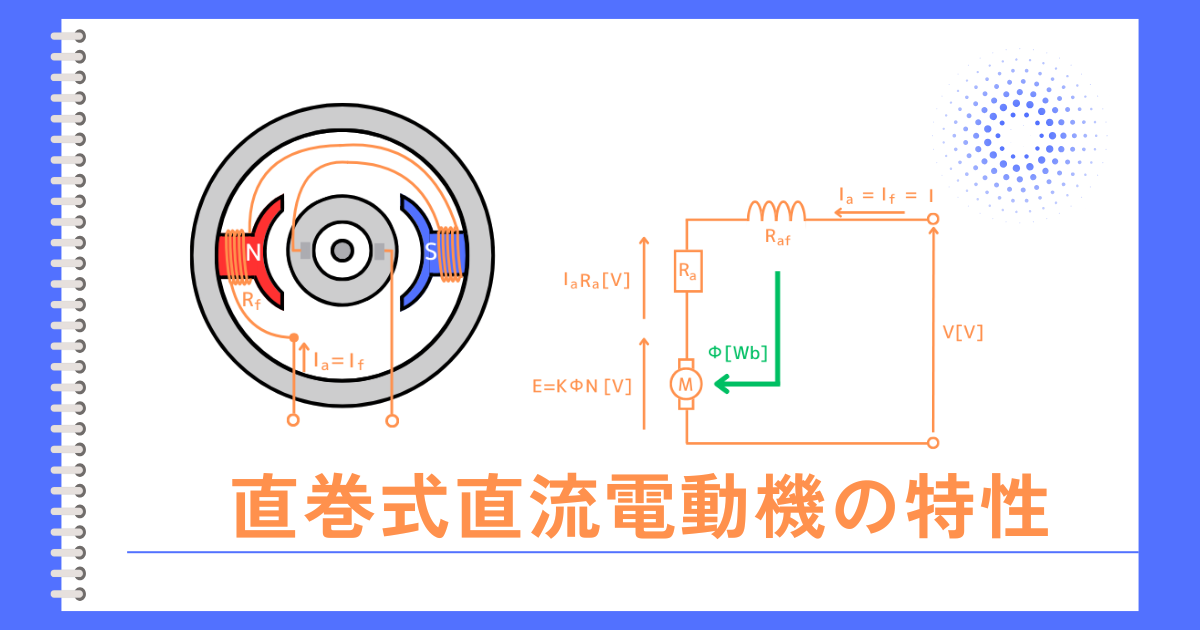
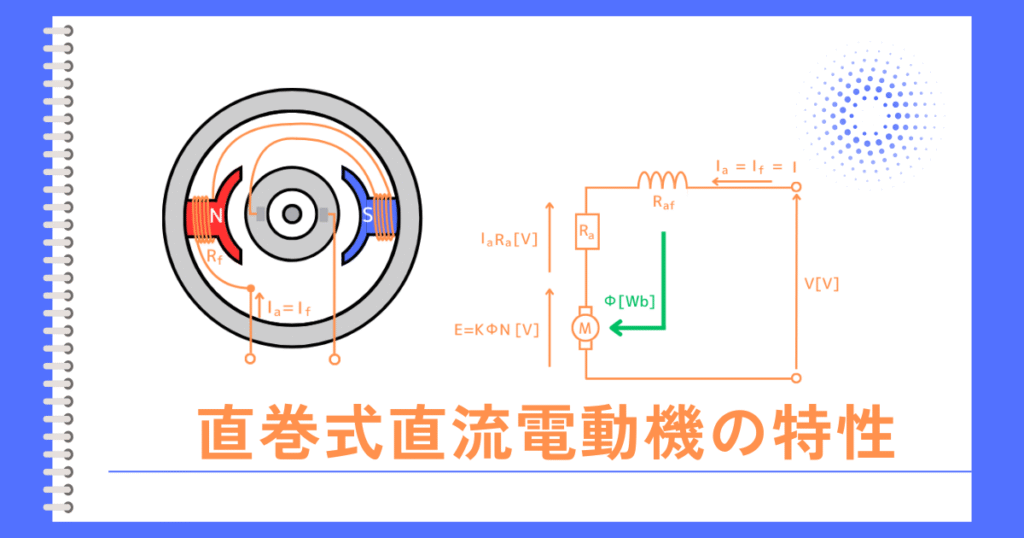
直巻式直流電動機は、左図のように、励磁回路が主回路と直列に接続されている直流電動機です。
特徴
・始動時・低速時に大きなトルクを得られる
・定出力特性(トルク\(T\)×回転数\(N\))
欠点
・無負荷運転を行うと、速度が上がり過ぎて過回転となり、故障する恐れがある。
そのため、無負荷運転になるような用途には使用出来ない。
・負荷変動によって回転数も変動する特性のため、定速度運転には向かない。
用途
クレーンなどの建設機械、電動ドリル、昔の鉄道(近年は誘導電動機が主流)のような、始動時(低速時)に高トルクが必要な用途に使用されます。
公式まとめ
電圧の基本式
\(V=E+I_a(R_a+R_{af})\)
逆起電力の重要式(参考:直流機の回転数のページ)
\(E=K \Phi N\)
速度特性式(導出すれば良いので覚える必要はない)
\(\displaystyle N=\frac{V}{K k’I_a} -\frac{R_a+R_{af}}{K k’}\)
トルク特性式(導出すれば良いので覚える必要はない)
\(T=K_T k’ I^2_a\)
記号の意味一覧
\(V[V]\):入力電圧
\(E[V]\):電機子導体に発生する逆起電力
\(I_a[A]\):負荷電流(電機子電流)
\(I_f[A]\):励磁電流
\(R_a[Ω]\):電機子導体の抵抗
\(N[min^{-1}]\):1分間あたりの回転数
\(T[Nm]\):トルク
\(\Phi[Wb]\):励磁回路で作り出した界磁磁束
\(K\):比例定数(速度特性)
\(K_T\):比例定数(トルク特性)
\(k’\):比例定数(磁束・励磁電流)
回路と特性
回路図
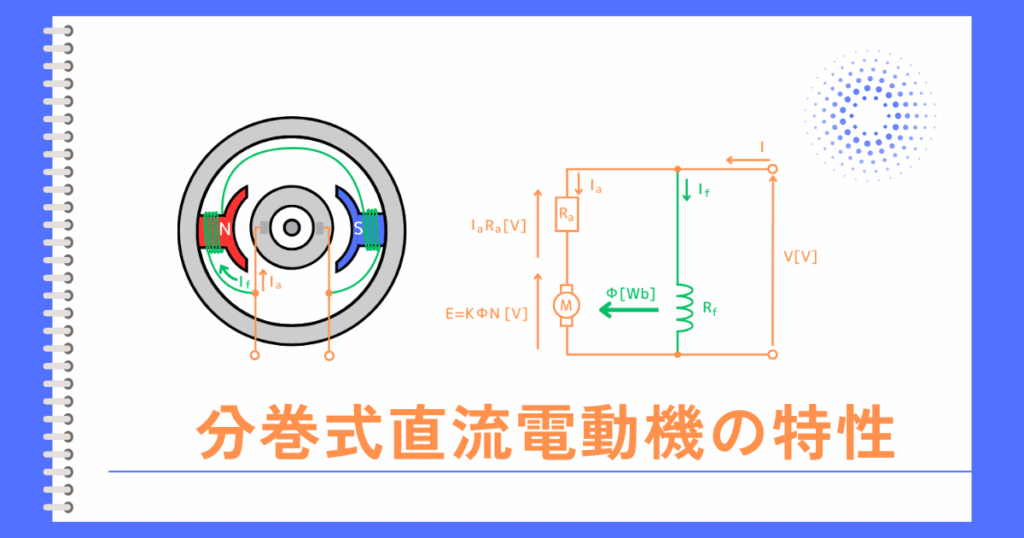
直流機の構造図から、回路図に書き変えると、次のようになります。

➡
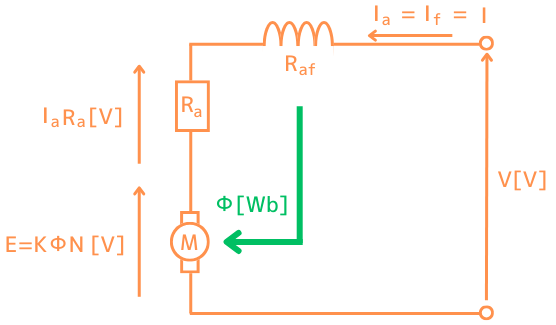
回路図から分かること
・界磁巻線と電機子が直列に接続されているため、
励磁電流\(I_f\) = 電機子電流\(I_a\) = 入力電流\(I\)
➡界磁磁束\(\Phi\)は、励磁電流に比例するので、電機子電流にも比例します。
➡負荷によって電機子電流が変動するので、界磁磁束も変動します。
➡界磁磁束が変動することにより、速度特性・トルク特性に影響を与えます。
速度特性
主回路の電圧の基本式は、直流機の回路図から次の①式であることがわかります。
\(V=E+I_a(R_a+R_{af})\) …①
直流機が回転することによって発生する逆起電力\(E[V]\)は、磁束\(\Phi[Wb]\)と、回転数\(N[min^{-1}]\)に比例するので、比例定数を\(K\)とすると、②式で表されます。
\(E=K \Phi N\) …②
②式を①式に代入し、回転数について整理すると、
\(V=K \Phi N+I_a(R_a+R_{af})\)
⇔ \(\displaystyle N=\frac{V-I_a(R_a+R_{af})}{K \Phi}\) …③
磁束\(\Phi[Wb]\)は、励磁電流\(I_f\)に比例するので、その比例定数を\(k’\)とすると、
\(\Phi=k’I_f\) …④
そして、励磁回路と、電機子回路は直列接続されているため、
励磁電流\(I_f\)、負荷電流\(I_a\)の関係は、
\(I_f=I_a\) …⑤
③式に、④・⑤式を代入すると、
\(\displaystyle N=\frac{V-I_a(R_a+R_{af})}{K k’I_a}\)
➡ \(\displaystyle N=\frac{V}{K k’I_a}\)\(\displaystyle -\frac{R_a+R_{af}}{K k’}\) …⑥
⑥式から、負荷電流\(I_a[A]\)と、回転数\(N[min^{-1}]\)が反比例することがわかります。
負荷電流\(I_a\)-回転数\(N\)特性
下図は、⑥式を
・負荷電流\(I_a[A]\)を横軸
・回転数\(N[min^{-1}]\)を縦軸
として、グラフ化したものです。
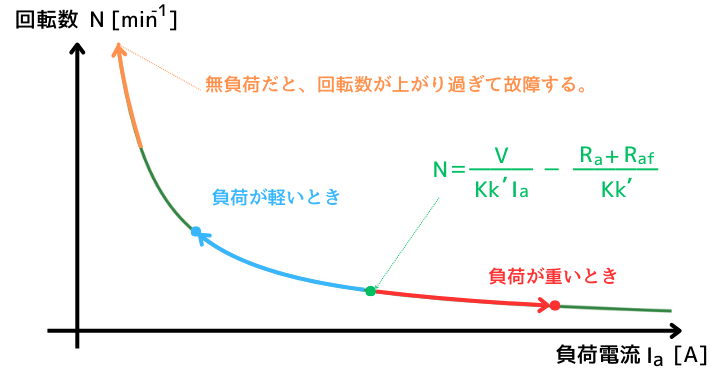
回転数\(N[min^{-1}]\)は、負荷電流\(I_a[A]\)に反比例するため、無負荷になると極端に回転数が上がってしまうため、電動機の故障につながります。
トルク特性
トルク特性は次式で表されます。
\(T=K_T \Phi I_a\) …⑦
主回路(電機子巻線)と、励磁回路は直列接続なので、界磁磁束\(\Phi[Wb]\)は負荷の重さによって大きく異なります。④・⑤式を⑦式に代入すると、
\(T=K_T k’ I^2_a\) …⑧
⑧式から、トルク\(T\)の大きさは負荷電流\(I_a\)の二乗に比例することがわかります。
下図は、⑧式をグラフ化したものです。
負荷が重くなるほど、負荷電流\(I_a[A]\)は増加します。
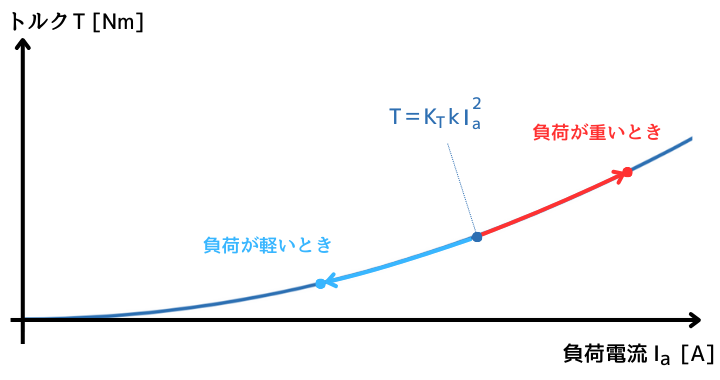
負荷電流\(I_a\)の二乗に比例してトルク\(T[Nm]\)が増加するので、非常に大きな負荷に対しても回転させる力が強いことがわかります。
速度とトルクの釣り合い
回転数は負荷電流と反比例の関係であり、トルクは負荷電流の二乗に比例する関係です。
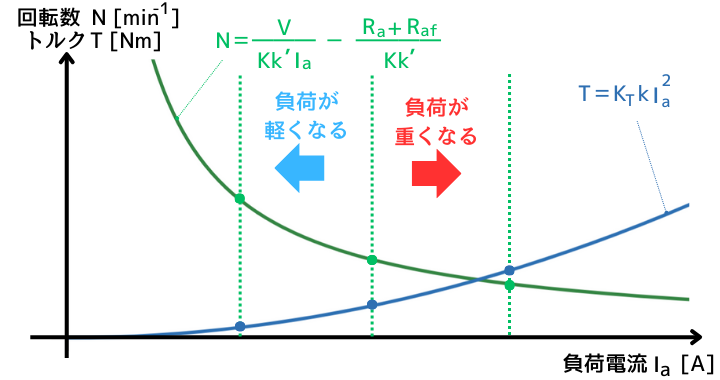
グラフに重ねて表示します。
負荷の大きさから必要なトルク\(T\)が決まります。
必要トルク\(T\)が決まると、トルクの式
\(T=K_T k’ I^2_a\)
から、負荷電流\(I_a\)が決まります。
負荷電流\(I_a\)が決まると、回転数の式
\(N=\frac{V-I_aR_a}{K \Phi}\)
から、回転数\(N\)が決まります。
鉄道に直巻式直流機が使用された場合を考えてみます。
停止状態から始動するときは必要なトルクは最も大きい状態です。
このとき、大きな負荷電流\(I_a\)が流れる事で、負荷電流の二乗に比例する大きな始動トルクが得られます。
そして、負荷電流が大きいときの回転数は低く、始動直後の低い回転数を徐々に加速していく事が出来ます。
このような始動特性から、直巻式直流電動機は、鉄道に適した特性であることがわかります。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
電験三種の領域をずっと超えた先の話を9割方しているので、電験三種の勉強の参考書としての購入はおすすめしません。
直流電動機について、ありとあらゆる事を書き記していった一冊です。
この本より詳しい本は少ないと思いますので、直流電動機の設計を学ぶ人に取っては良い本かと思われます。
感覚的には、研究論文化する内容ではないけど、後世には残しておきたいと思ったことをまとめたというような感じでしょうか。
文章の癖は強いので、もし買う場合はサンプルを読んでから購入することを推奨します。






コメント