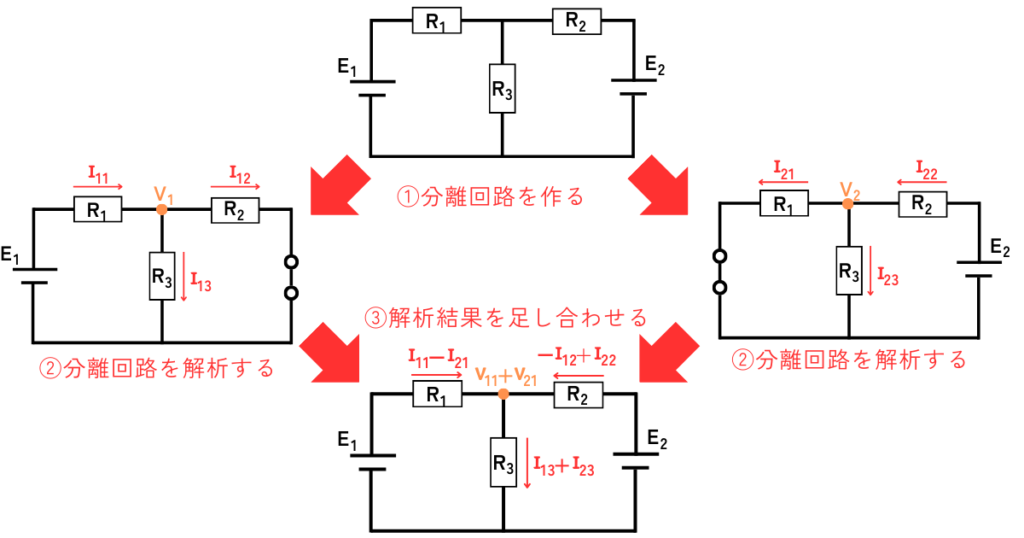
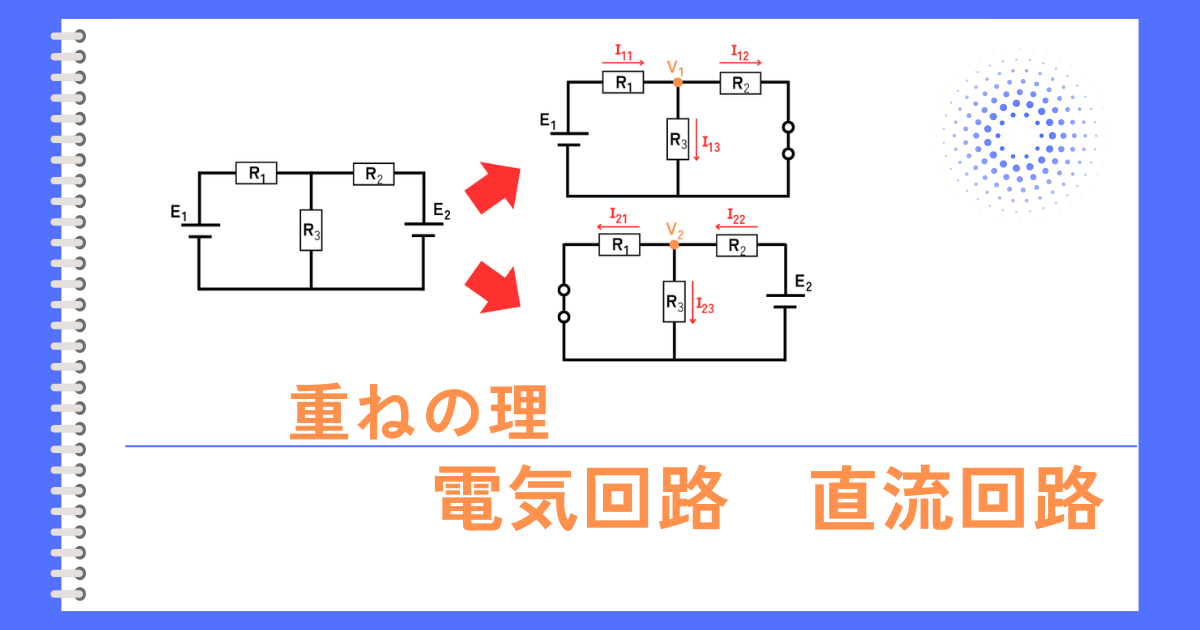
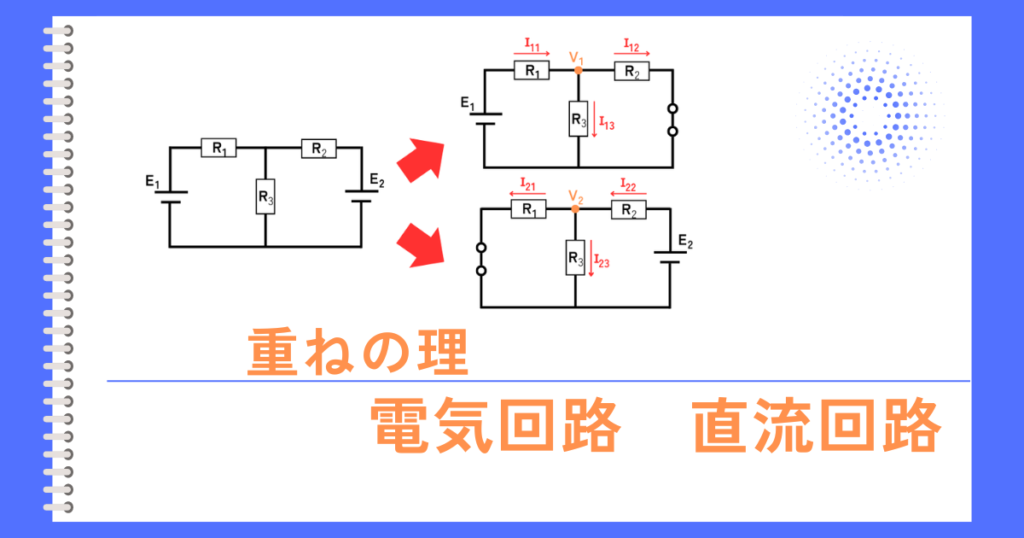
重ねの理とは
2つ以上の電源が接続された回路において、各部に流れる電流や、各部に印加される電圧は、その回路の電源が1つだけつながっているときの解析した結果を足し合わせ(重ね合わせ)たものに等しいという定理です。
重ねの理を使わずに2つ以上の電源が接続された回路のまま解析しようとすると、キルヒホッフの法則を多くの方程式からなる連立方程式を解かなければならないので、解析に手間が掛かります。
重ねの理を使うことで、連立方程式の立式と、その解を求める手間がなくなるので、簡単に解析することができます。
重ねの理の手順
次の3段階の手順を踏むことで回路が解析できます。
1. 電源毎の分離回路を作る。
2. 分離回路毎に各電流、電圧を解析する。
3. 解析結果を足し合わせる。
電圧源の重ねの理の実例
重ねの理の使い方の例
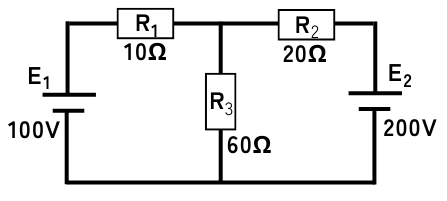
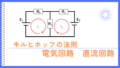
言葉で説明するよりも、実際に例題を解く方がわかりやすいと思うので、下図のような回路の例を用いて説明します。
2つの電圧源を使用した回路に、重ねの理を用いて各部の電圧・電流を解析します。
1.電源毎の分離回路を作る
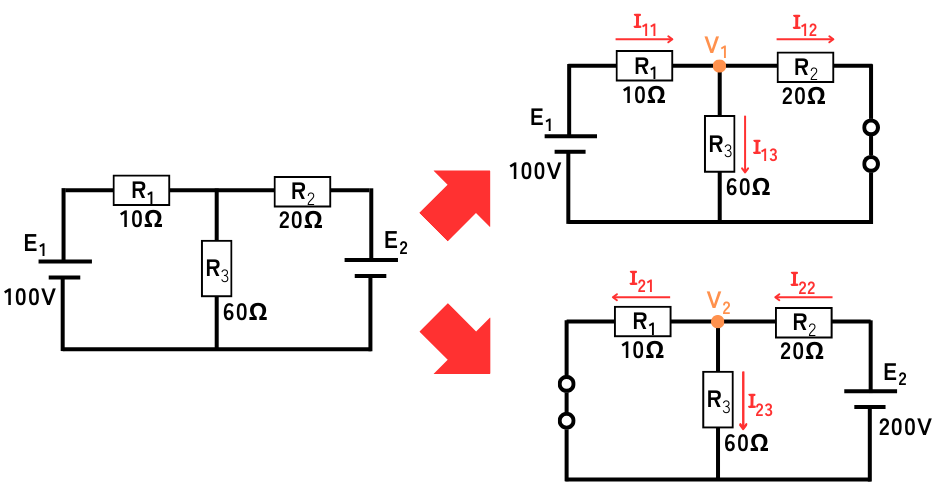
電圧源が\(E_1\)だけの回路、電圧源が\(E_2\)だけの回路の2つの回路を作ります。
考慮しないほうの電圧源は「短絡」します。
2.分離回路を解析する
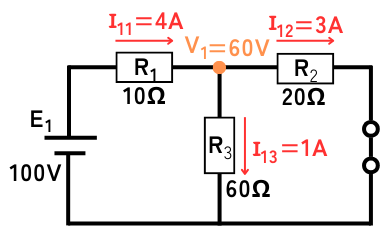
\(R_2\)と\(R_3\)の合成抵抗を\(R_{23}\)とすると、
\(\displaystyle R_{23}=\frac{R_2R_3}{R_2+R_3}=\frac{20・60}{20+60}=15Ω\)
全ての抵抗の合成抵抗を\(R\)とすると、
\(\displaystyle R=R_1+R_{23}=10+15=25Ω\)
各部の電圧、電流を求めます。
\(V_1=\frac{R_{23}}{R_1+R_{23}}E_1=\frac{15}{25}100=60V\)
\(I_{11}=\frac{E_1}{R}=\frac{100}{25}=4A\)
\(I_{12}=\frac{V_1}{R_2}=\frac{60}{20}=3A\)
\(I_{13}=\frac{V_1}{R_3}=\frac{60}{60}=1A\)
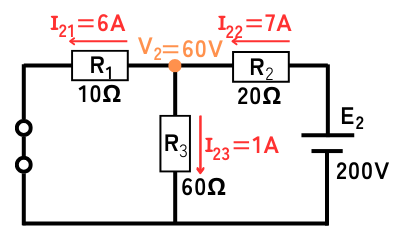
\(R_1\)と\(R_3\)の合成抵抗を\(R_{13}\)とすると、
\(\displaystyle R_{13}=\frac{R_1R_3}{R_1+R_3}=\frac{10・60}{10+60}=8.57Ω\)
全ての抵抗の合成抵抗を\(R’\)とすると、
\(\displaystyle R’=R_2+R_{13}=20+8.57=28.57Ω\)
各部の電圧、電流を求めます。
\(V_2=\frac{R_{13}}{R_2+R_{13}E_2}=\frac{8.57}{28.57}200=60V\)
\(I_{21}=\frac{V_1}{R_1}=\frac{60}{10}=6A\)
\(I_{22}=\frac{E_2}{R}=\frac{200}{28.57}=7A\)
\(I_{23}=\frac{V_1}{R_3}=\frac{60}{60}=1A\)
3.解析結果を足し合わせる
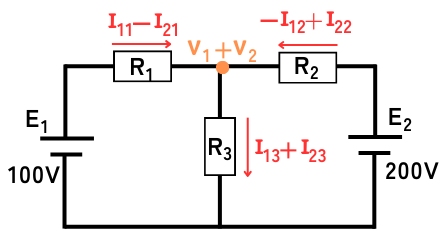
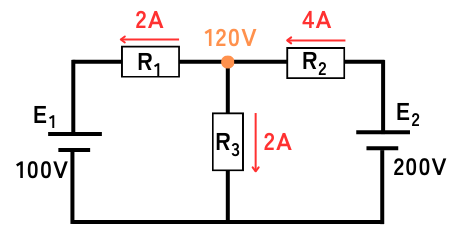
解析した分離回路の解析結果を足し合わせます。
正負の符号や、電流の向き等に気を付けて足し合わせる必要があります。
\(V_1+V_2=60+60=120V\)
\(I_{11}-I_{21}=4-6=-2A\)
\(I_{11}-I_{21}\)は左から右へ流れる方向を正としています。
負となるため、右から左に\(2A\)の電流が流れています。
\(-I_{12}+I_{22}=-3+7=4A\)
\(-I_{12}+I_{22}\)は右から左へ流れる方向を正としています。正であるため、右から左に\(4A\)の電流が流れています。
\(I_{13}+I_{23}=1+1=2A\)
\(I_{13}+I_{23}\)は上から下へ流れる方向を正としています。正であるため、上から下に\(2A\)の電流が流れています。
電流源の重ねの理の実例
重ねの理の使い方の例
言葉で説明するよりも、実際に例題を解く方がわかりやすいと思うので、下図のような回路の例を用いて説明します。
2つの電流源を使用した回路に、重ねの理を用いて各部の電圧・電流を解析します。
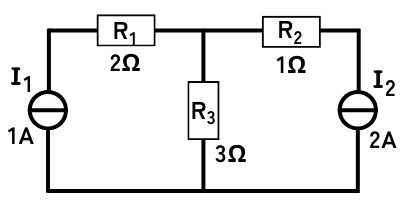
1.電源毎の分離回路を作る
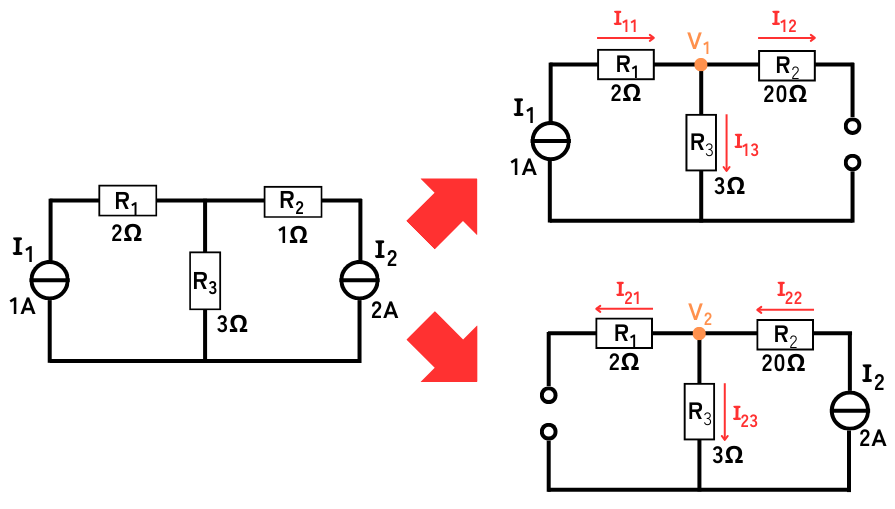
電流源が\(I_1\)だけの回路、電流源が\(I_2\)だけの回路の2つの回路を作ります。
考慮しないほうの電流源は「開放」します。
2.分離回路を解析する
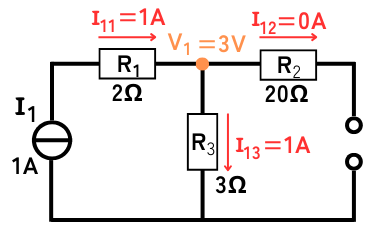
各部の電圧、電流を求めます。
電流源\(I_2\)は「開放」するので、\(I_1\)から出てきた電流は全て\(R_1\)、\(R_3\)を通って\(I_1\)に戻ります。
\(I_{11}=1A\)
\(I_{12}=0A\)
\(I_{13}=1A\)
\(V_1=I_{13}R_3=3V\)
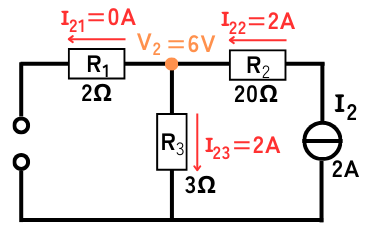
各部の電圧、電流を求めます。
電流源\(I_1\)は「開放」するので、\(I_2\)から出てきた電流は全て\(R_2\)、\(R_3\)を通って\(I_2\)に戻ります。
\(I_{21}=0A\)
\(I_{22}=2A\)
\(I_{23}=2A\)
\(V_2=I_{23}R_3=6V\)
3.解析結果を足し合わせる
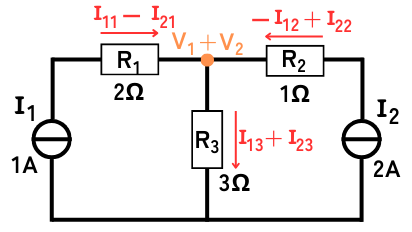
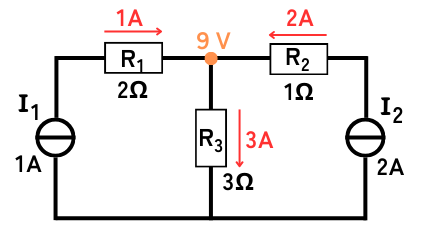
解析した分離回路の解析結果を足し合わせます。
正負の符号や、電流の向き等に気を付けて足し合わせる必要があります。
\(V_1+V_2=3+6=9V\)
\(I_{11}-I_{21}=1-0=1A\)
\(I_{11}-I_{21}\)は左から右へ流れる方向を正としています。
正となるため、左から右に\(1A\)の電流が流れています。
\(-I_{12}+I_{22}=-0+2=2A\)
\(-I_{12}+I_{22}\)は右から左へ流れる方向を正としています。正であるため、右から左に\(2A\)の電流が流れています。
\(I_{13}+I_{23}=1+2=3A\)
\(I_{13}+I_{23}\)は上から下へ流れる方向を正としています。正であるため、上から下に\(3A\)の電流が流れています。
過去問
難易度 ★★☆☆☆
| 電験三種 令和5年度下期 問6 | 2電源回路の解析 |
| 電験三種 令和5年度上期 問5 | 2電源回路の解析 |
| 電験三種 令和5年度上期 問6 | 電圧源・電流源からなる2電源回路の解析 |
関連記事(直流回路に関する解説)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント