概要
熱電子に関する計算・論説問題です。
基本的には平行平板コンデンサの問題なので、電磁気学を勉強していれば解けると思います。
キーワード
平行平板コンデンサ、熱電子
問題
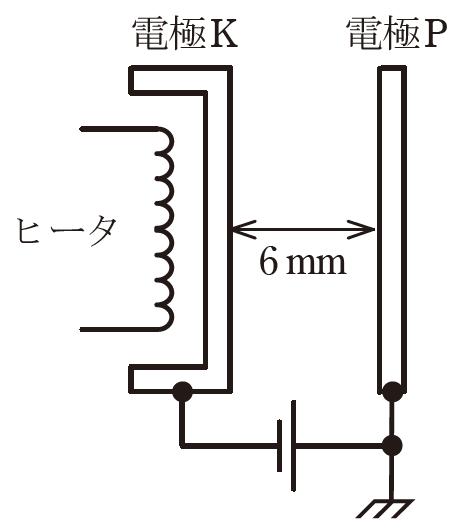
真空中において、図のように電極板の間隔が6 mm、電極板の面積が十分広い平行平板電極があり、電極K、P 間には\(2000 V\) の直流電圧が加えられている。
このとき、電極K、P 間の電界の強さは約 \( \fbox{(ア)}\) \(V/m\) である。
電極K をヒータで加熱すると表面から \( \fbox{(イ)}\) が放出される。
ある1個の電子に着目してその初速度を零とすれば、電子が電極Pに達したときの運動エネルギーW は \( \fbox{(ウ)}\) \(J\) となる。
ただし、電極 K、P 間の電界は一様とし、電気素量\(e=1.6×10^{-19} C\) とする。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる語句又は数値の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
|---|---|---|---|
| (1) | \(3.3×10^2\) | 光電子 | \(1.6×10^{-16}\) |
| (2) | \(3.3×10^5\) | 熱電子 | \(1.6×10^{-16}\) |
| (3) | \(3.3×10^2\) | 光電子 | \(3.2×10^{-16}\) |
| (4) | \(3.3×10^2\) | 熱電子 | \(1.6×10^{-16}\) |
| (5) | \(3.3×10^5\) | 熱電子 | \(3.2×10^{-16}\) |
答え
(5)
解説テキスト リンク
回答解説
\( \fbox{(ア)}\)
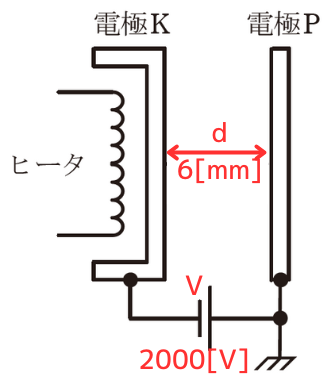
電界の強さは、
\(E=\frac{V}{d}=\frac{2000}{6×10^{-3}}=3.3×10^5[V/m]\)
です。
したがって、(ア)は\(E=3.3×10^5[V/m]\)です。
\( \fbox{(イ)}\)
電極Kをヒータで加熱すると、電極表面から電子が放出されます。
この放出された電子を、(イ)熱電子と呼びます。
\( \fbox{(ウ)}\)
電子の電荷量は、\(e=1.6×10^{-19}\)、電位\(V\)は、単位電荷の位置エネルギー(ポテンシャルエネルギー)なので、運動エネルギー\(W\)は、
\(W=eV=1.6×10^{-19}・2000=3.2×10^{-16}\)
したがって、(ウ)は\(W=3.2×10^{-16}[J]\)です。
以上より、(5)が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和7年度上期 第三種電気主任技術者試験 理論科目問12
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント