概要
コンデンサの計算問題です。
難しくはない問題ですが、コンデンサに関する公式を一通り理解しておく必要があります。
キーワード
コンデンサ、コンデンサの並列接続、静電容量
問題
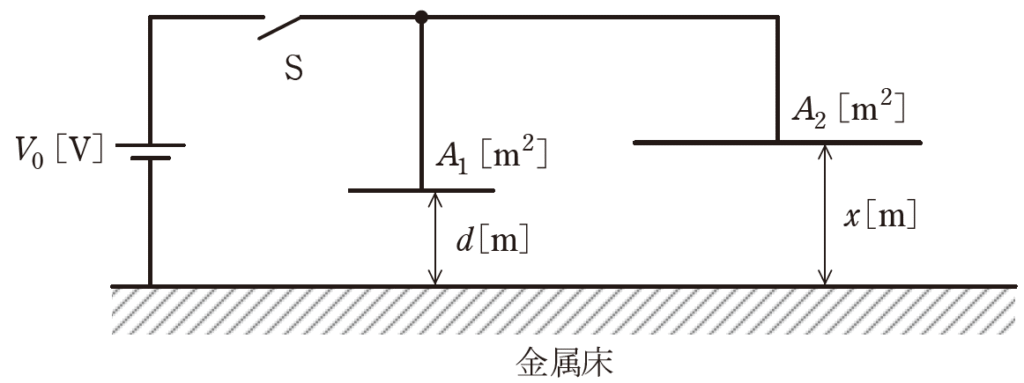
図のように、十分大きい平らな金属板で覆われた床と平板電極とで作られる空気コンデンサが二つ並列接続されている。
二つの電極は床と平行であり、それらの面積は左側が\(A_1=10^{-3}m^2\)、右側が\(A_2=10^{-2}m^2\)である。
床と各電極の間隔は左側が\(d=10^{-3}m\)で固定、右側が\(x[m]\)で可変、直流電源電圧は\(V_0=1000V\)である。
次の(a)及び(b)の問に答えよ。
ただし、空気の誘電率を\(ε=8.85×10^{-12}F/m\)とし、静電容量を考える際にコンデンサの端効果は無視できるものとする。
(a) まず、右側の\(x[m]\)を\(d[m]\)と設定し、スイッチSを一旦閉じてから開いた。
このとき、二枚の電極に蓄えられる合計電荷Qの値[C]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)\(8.0×10^{-9}\) (2)\(1.6×10^{-8}\) (3)\(9.7×10^{-8}\)
(4)\(1.9×10^{-7}\) (5)\(1.6×10^{-6}\)
(b) 上記(a)の操作の後、徐々にxを増していったところ\(x=3.0×10^{-3}m\)のときに左側の電極と床との間に火花放電が生じた。左側のコンデンサの空隙の絶縁破壊電圧Vの値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)\(3.3×10^2\) (2)\(2.5×10^3\) (3)\(3.0×10^3\)
(4)\(5.1×10^3\) (5)\(3.0×10^4\)
答え
(a)(3)
(b)(2)
解説テキスト リンク
回答解説
(a)問題の解答の流れ
①両方の電極の静電容量\(C_1\)、\(C_2\)を求める
②両方の電極の電荷量\(Q_1\)、\(Q_2\)を求める
③合計電荷\(Q\)を求める
①両方の電極の静電容量\(C_1\)、\(C_2\)を求める
問題文から、
・\(ε=8.85×10^{-12}F/m\)
・\(A_1=10^{-3}m^2\)
・\(A_2=10^{-2}m^2\)
・\(d=10^{-3}m\)
です。
左側電極の静電容量を\(C_1\)として、各パラメータを代入していくと、
\(\displaystyle C_1=ε\frac{A_1}{d}=8.85×10^{-12}\frac{10^{-3}}{10^{-3}}=8.85×10^{-12}[F]\)
右側電極の静電容量を\(C_2\)として、各パラメータを代入していくと、
\(\displaystyle C_2=ε\frac{A_2}{d}=8.85×10^{-12}\frac{10^{-2}}{10^{-3}}=8.85×10^{-11}[F]\)
②両方の電極の電荷量\(Q_1\)、\(Q_2\)を求める
電圧は\(V_0=1000V\)なので、
左側電極の電荷量\(Q_1\)は、
\(\displaystyle Q_1=C_1V_0=8.85×10^{-12}×10^3=8.85×10^{-9}\)
右側電極の電荷量\(Q_2\)は、
\(\displaystyle Q_2=C_2V_0=8.85×10^{-11}×10^3=88.5×10^{-9}\)
③合計電荷\(Q\)を求める
二つの電極は並列接続されているので、合計電荷\(Q[C]\)は次のようにもとめられます。
\(Q=Q_1+Q_2=8.85×10^{-9}+88.5×10^{-9}=9.7×10^{-8}\)
以上より、(a)問題は(3)\(9.7×10^{-8}\) が答えです。
(b)問題の解答の流れ
①右側極板の距離を\(x=3×10^{-3}[m]\)にしたときの静電容量\(C’_2\)を求める
②直列・並列の合成容量を求めていく
①右側極板の距離を\(x=3×10^{-3}[m]\)にしたときの静電容量\(C’_2\)を求める
右側極板の距離を\(x=3×10^{-3}[m]\)にしたときの静電容量\(C’_2\)は、
\(\displaystyle C’_2=ε\frac{A_2}{x}=8.85×10^{-12}\frac{10^{-2}}{3×10^{-3}}=29.5×10^{-12}\)
②電圧が\(V’\)に変化したときの各極板の電荷の式を求める
右側極板の距離を\(x=3×10^{-3}[m]\)にしたときの極板に印加される電圧は\(V’\)に変化します。
左側極板の電荷量\(Q’_1\)は、\(Q’_1=C_1V’\)
右側極板の電荷量\(Q’_2\)は、\(Q’_2=C’_2V’\)
③合計電荷\(Q[C]\)が変化しないことから電圧\(V’\)を求める
合計電荷\(Q[C]\)は、スイッチSを開いていることから増えも減りもしません。
そのため、(a)問題のときから変わらず\(Q=9.7×10^{-8}[C]\)です。
\(Q=Q’_1+Q’_2=C_1V’+C’_2V’=9.7×10^{-8}\)
⇔ \(\displaystyle V’=\frac{9.7×10^{-8}}{C_1+C’_2}=\frac{9.7×10^{-8}}{38.35×10^{-12}}=2.5×10^3\)
以上より、(b)問題は(2)\(2.5×10^3\) が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和6年度下期 第三種電気主任技術者試験 理論科目B問題問17
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント