難易度
磁界に関する基礎知識があれば解ける論説問題です。
基礎レベルなので、確実に解けるようになりましょう。
問題
磁界及び磁束に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
(1) 1m当たりの巻数がNの無限に長いソレノイドに電流\(I[A]\)を流すと,
ソレノイドの内部には磁界\(H=NI[A/m]\)が生じる。
磁界の大きさは、ソレノイドの寸法や内部に存在する物質の種類に影響されない。
(2) 均一磁界中において、磁界の方向と直角に置かれた直線状導体に直流電流を流すと、
導体には電流の大きさに比例した力が働く。
(3) 2本の平行な直線状導体に反対向きの電流を流すと、
導体には導体間距離の2乗に反比例した反発力が働く。
(4) フレミングの左手の法則では、親指の向きが導体に働く力の向きを示す。
(5) 磁気回路において、透磁率は電気回路の導電率に、磁束は電気回路の電流にそれぞれ対応する。
答え
(3)
要点整理
無限長ソレノイドが作る磁界
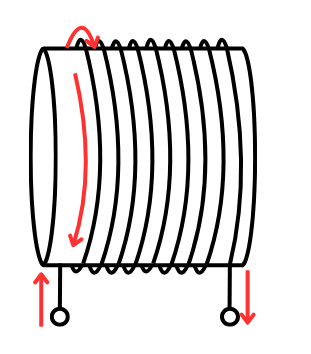
ソレノイドコイル
結論
無限長ソレノイドが作る磁界強度は\(H=nI[A/m]\)です。
・\(n\)[回/m]は、1m当たりのコイルの巻き数。
・\(I[A]\)は、コイルに流れる電流値です。
この式から、コイルの半径は磁界の強さに影響を与えず、1m当たりのコイルの巻数のみが影響することがわかります。
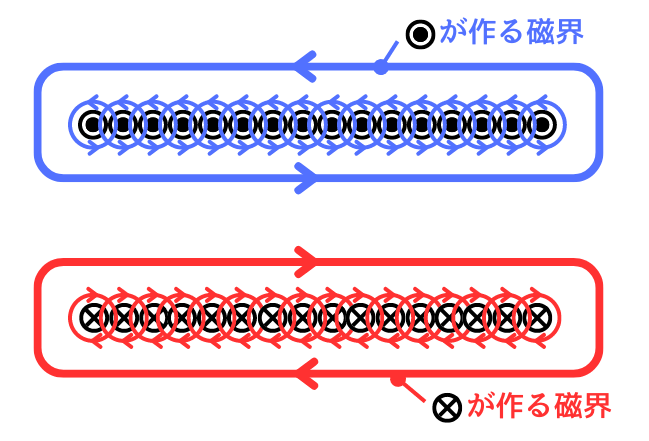
\(H=nI[A/m]\)の式を示していきます。
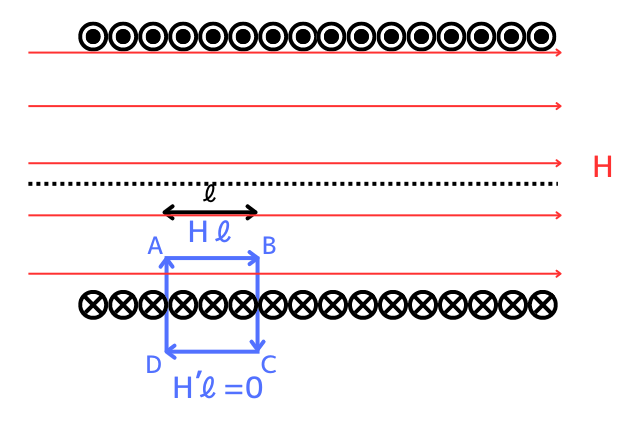
左図は、ソレノイドの断面を示した図です。

は、画面奥から手前に向かう方向の電流を示し、青線の磁界を作ります。

は、画面手前から奥に向かう方向の電流を示し、赤線の磁界を作ります。
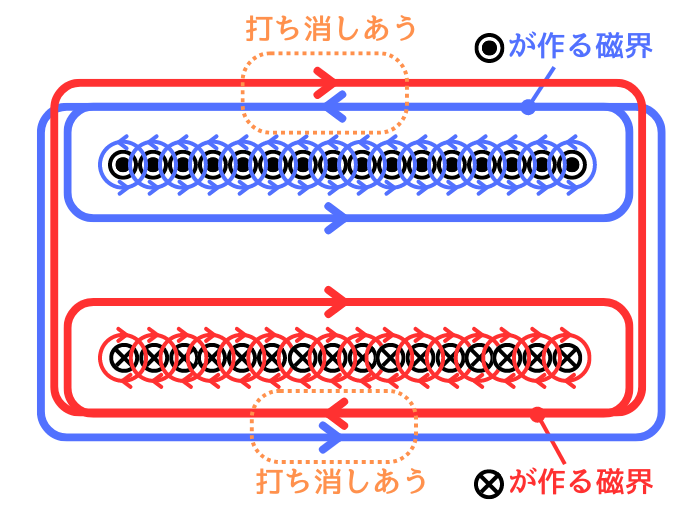
上側と下側のコイル間は、同じ方向の磁界を作り出します。
しかし、コイルの外側は、上下のコイルの作り出す磁界が逆方向を向いているため、打ち消しあい、磁界は0となります。
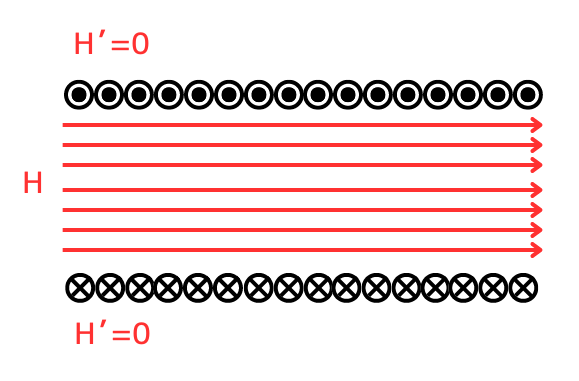
作り出した磁界が合成された結果を示すと、左図のように、
コイル内部の磁界は\(H[A/m]\)
コイル外部の磁界は\(H’=0[A/m]\)
となります。
アンペールの法則を使って、ソレノイドの作る磁界の強さ\(H\)を求めます。
アンペールの法則は、閉じた経路に沿って磁界の強さ\(H\)を足し合わせた結果は閉じた経路を貫く電流の和に比例するという法則です。
A→B間、C→D間の長さは\(l[m]\)として、図のA→B→C→D→Aの閉じた経路の磁界の強さを足し合わせます。
・A→B:磁界強度\(H\)の磁力線に沿い、距離は\(l\)なので、\(Hl\)です。
・B→C:磁力線と垂直なので、0です。
・C→D:ソレノイドの外側は磁界を打ち消しあって無い(\(H’=0\))ので磁界の強さは0です。
・D→A:磁力線と垂直なので、0です。
以上より、A→B→C→D→Aの経路の磁界の強さを足し合わせた結果は、\(Hl+0+0+0=Hl\)です。
次に、A→B→C→D→Aの経路を貫く電流の和を求めます。
A→B→C→D→Aの経路囲まれる導線の本数は\(n[回/m]×l[m]=nl[回]\)です。
導線1本辺りに流れる電流は\(I[A]\)だから、A→B→C→D→Aの経路囲まれる電流の和は\(nlI\)です。
以上より、アンペールの法則から、
\(Hl=nlI\)
⇔\(H=nI\)
と、求まります。
電磁力について
電磁力は、電流と磁界の相互作用によって発生した力です。電磁力\(\vec{F}[N]\)は、電流\(\vec{I}[A]\)と、磁束密度\(\vec{B}[T]\)の外積で表されます。これを式で表すと、\(\vec{F}=\vec{I}\times\vec{B}\)となります。
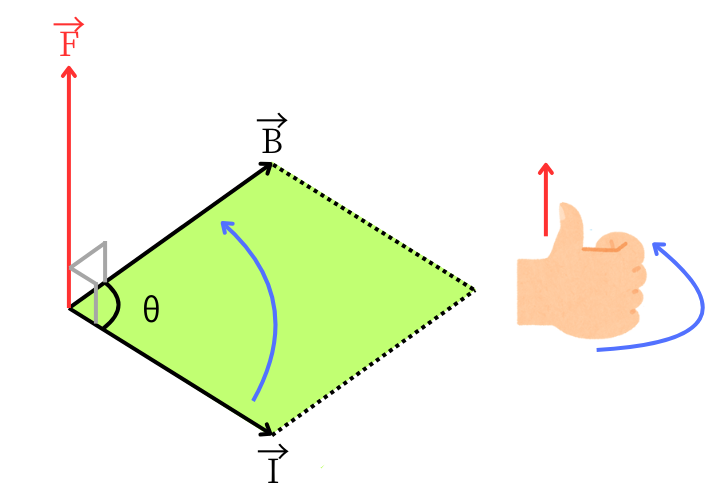
電磁力の向きは、電流の向きから、磁界の向きに右ねじの法則で回したときに、親指が向く向きです。
\(\vec{F}\)の大きさは、\(\vec{I}\)と\(\vec{B}\)の作る平行四辺形の面積と同じです。
つまり、\(|F|=|I| |B| sinθ\)です。導体の長さを\(l[m]\)とすると\(F=IBlsinθ\)と求まります。
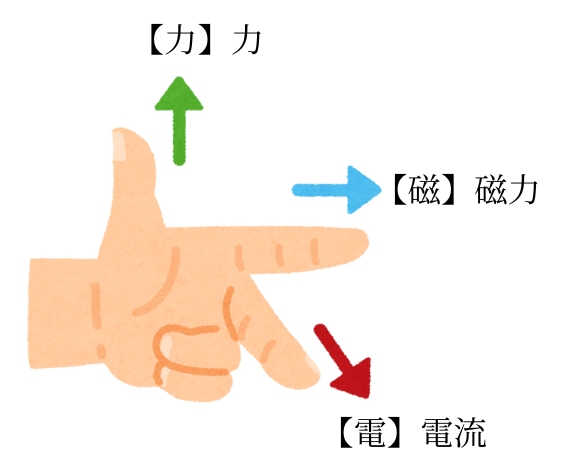
上記で示した電流・磁界・力の向きを簡単に表現すると、フレミング左手の法則で示されます
磁気回路と電気回路
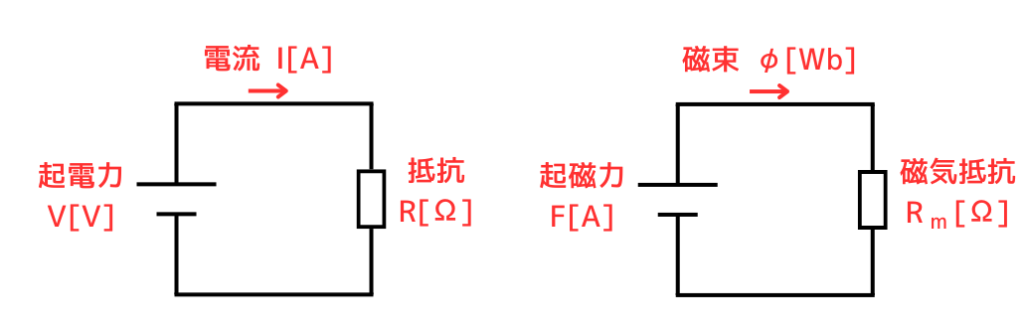
磁気回路にも、電気回路のようにオームの法則とキルヒホッフの法則がなりたちます。
| 電気回路 - 磁気回路対応表 | |
|---|---|
| 電気回路 | 磁気回路 |
| 起電力\(V[V]\) | 起磁力\(F[A]\) |
| 電流\(I[A]\) | 磁束\(φ[Wb]\) |
| 抵抗\(R[Ω]\) (レジスタンス) | 磁気抵抗\(R_m[H^{-1}]\) (リラクタンス) |
| オームの法則 \(V=IR\) | オームの法則 \(F=φR_m\) |
起磁力の関係式
\(N\)回巻のコイルに流れる電流\(I[A]\)が起磁力を生み出すので、起磁力\(F[A]\)は、
\(F=NI[A]\) ………①
です。
磁気回路の起磁力を生み出すコイル部分は、無限長ソレノイドとして扱います。
そのため、磁界の強さ\(H[A/m]\)、磁気回路の長さ(磁路長)\(l[m]\)としたとき、
\(F=Hl\) ………②
です。①・②式から
\(NI=Hl\)
⇔\(\displaystyle H=\frac{NI}{l}\) ………③
磁束の関係式
磁束密度\(B[T]\)は、磁束\(φ[Wb]\)の密度なので、磁路の面積\(S[m^2]\)を使って表すと、
\(φ=BS[Wb]\) ………④
⇔\(\displaystyle B=\frac{φ}{S}\) ………⑤
です。
磁束密度\(B[T]\)と、磁界強度\(H[A/m]\)、透磁率\(μ[H/m]\)の関係式は、
\(B=μH\) ………⑥
磁気抵抗の関係式
①・③・⑥式から、
\(\displaystyle B=\frac{μNI}{l}=\frac{μF}{l}\)
となるので、⑤式を代入すると、
\(\displaystyle \frac{φ}{S}=\frac{μF}{l}\)
⇔\(\displaystyle R_m=\frac{F}{φ}=\frac{l}{μS}\)
以上より、\(\displaystyle R_m=\frac{l}{μS}\) が導出できました。
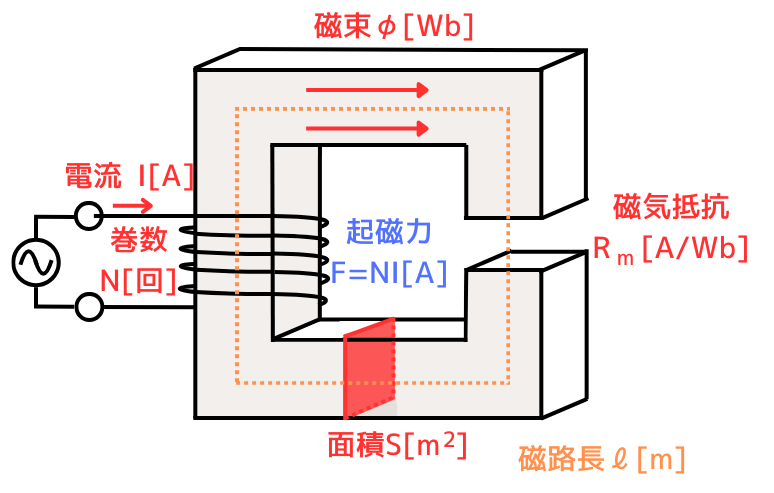
磁気回路の式をまとめます。
起 磁 力:\(F=NI[A]\)
磁 束:\(φ=BS[Wb]\)
磁気抵抗:\(\displaystyle R_m=\frac{l}{μS}[H^{-1}]\)
磁気抵抗:\(\displaystyle R_m=\frac{l}{μS}\)と、磁路について
①磁気回路の面積\(S\)が広くなれば、磁束\(φ\)が通る道は広くなります。
つまり、磁束が流れやすくなり、磁気抵抗\(R_m\)は小さくなります。
②磁路長\(l[m]\)が長くなると、磁束が流れる抵抗が増えるため、磁気抵抗\(R_m\)は大きくなります。
③透磁率\(μ\)は、磁束がどれくらい通しやすいかを表します。
透磁率\(μ\)が大きくなると、磁束が通りやすくなるので、磁気抵抗\(R_m\)は小さくなります。
つまり、磁気回路における透磁率は、電気回路における導電率に対応しています。
回答解説
(1) 1m当たりの巻数がNの無限に長いソレノイドに電流\(I[A]\)を流すと、
ソレノイドの内部には磁界\(H=NI[A/m]\)が生じる。
磁界の大きさは、ソレノイドの寸法や内部に存在する物質の種類に影響されない。
無限長ソレノイドが作る磁界の要点整理から、ソレノイド内部には\(H=NI[A/m]\)
が生じます。したがって、正しいです。
(2) 均一磁界中において、磁界の方向と直角に置かれた直線状導体に直流電流を流すと、
導体には電流の大きさに比例した力が働く。
長さ\(l[m]\)の導体に流れる電流\(I[A]\)と、磁界\(B[T]\)のなす角が\(θ\)の時に、
導体に働く力は、
\(F=IBlsinθ\)
です。
磁界と電流の向きが直角の時は、\(sinθ=1\)なので、\(F=IBl\)となります。
したがって、導体には電流の大きさに比例した力が働きますので正しいです。
(3) 2本の平行な直線状導体に反対向きの電流を流すと、
導体には導体間距離の2乗に反比例した反発力が働く。
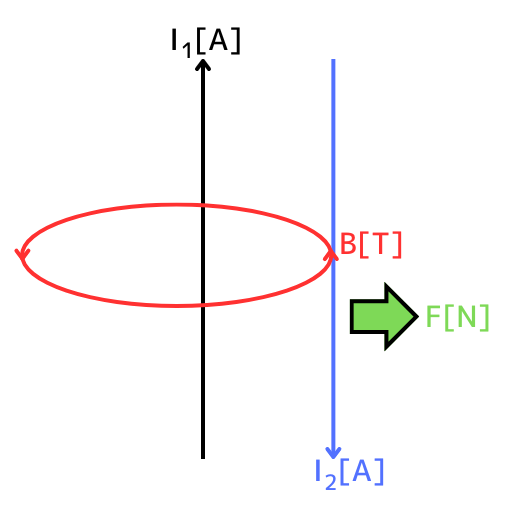
働く力の方向は、左図の通り、反発する方向です。
2本の導体のうち、左側の黒線の導体に流れる電流\(I_1[A]\)が作る磁界\(H_1[A/m]\)は、アンペールの法則から
\(I_1=\oint Hdl=Hl=H・2πr\)
⇔\(\displaystyle H=\frac{I_1}{2πr}\)
磁束密度\(B[T]\)と磁界の強さ\(H[A/m]\)の関係は、\(B=μH\)なので、
\(\displaystyle B=\frac{μI_1}{2πr}\)
導体に働く力\(F[N]\)は、
\(\displaystyle F=I_2Blsinθ=\frac{μI_1I_2}{2πr}\)
単位長さ当たりとするので、\(l=1[m]\)、電流と磁界は直角なので\(sinθ=1\)としました。
以上より、導体間距離に反比例した反発力が働くため、2乗に反比例は間違いです。
(4) フレミングの左手の法則では、親指の向きが導体に働く力の向きを示す。

左図の通り、親指の向きが導体に働く力の向きを示しますので正しいです。
(5) 磁気回路において、透磁率は電気回路の導電率に、磁束は電気回路の電流にそれぞれ対応する。
磁気回路と電気回路の要点整理に記載した通り、磁気回路における透磁率は、電気回路における
導電率に対応しますので正しいです。
以上より、(3)が答えです。
出典元
令和5年度第三種電気主任技術者試験 理論科目A問題上期問4
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント