概要
AM変調に関する計算、論説問題です。
無線通信について学んだことがある人には簡単な問題ですが、学んだことが無いと難しい問題です。
キーワード
AM変調,変調度,検波回路
問題
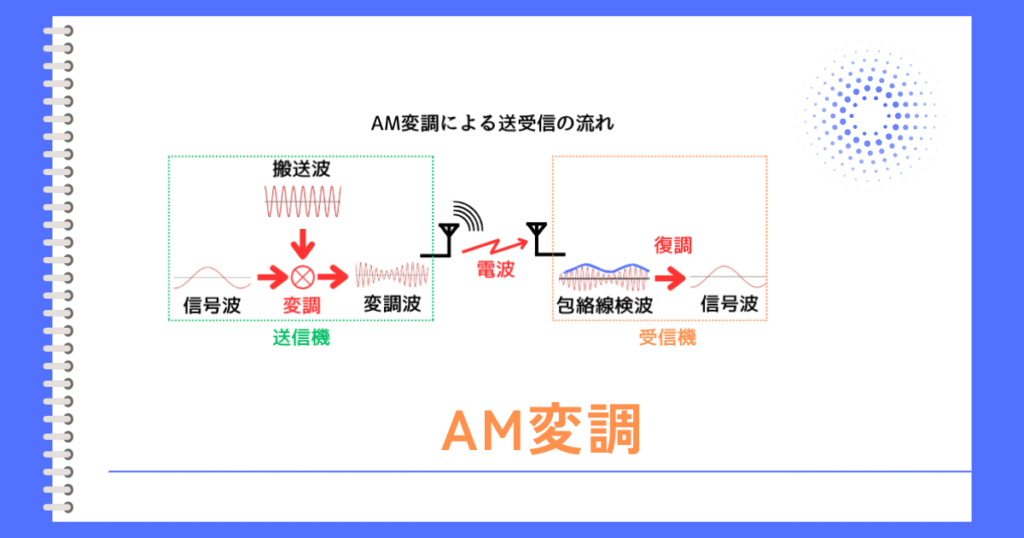
振幅変調について,次の(a)及び(b)の問に答えよ。
(a) 図1の波形は,正弦波である信号波によって搬送波の振幅を変化させて得られた変調波を表している。この変調波の変調度の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
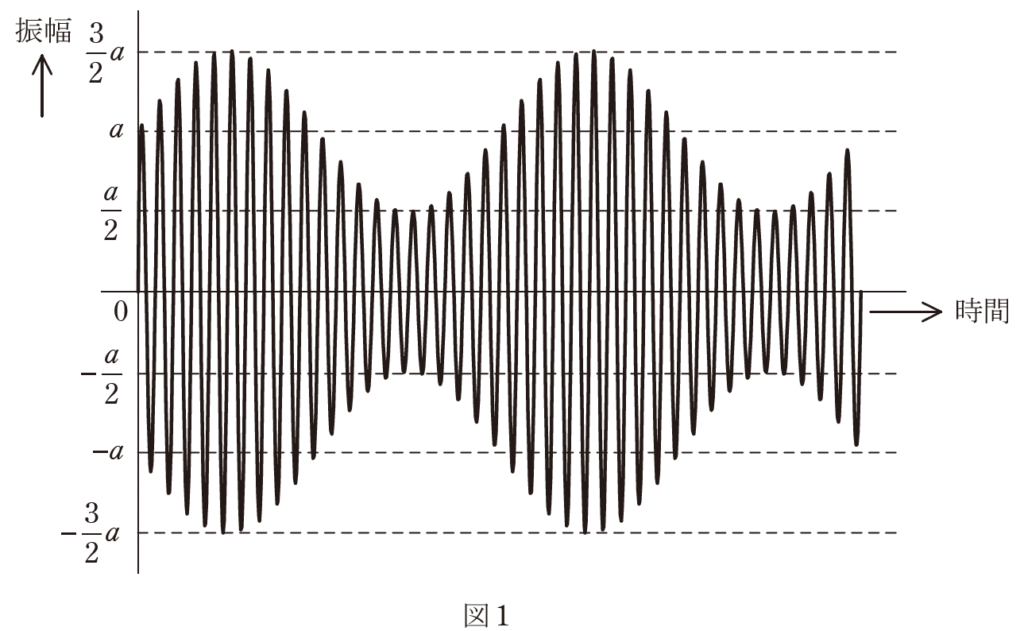
(1) 0.33 (2) 0.5 (3) 1.0 (4) 2.0 (5) 3.0
(b) 次の文章は、直線検波回路に関する記述である。
振幅変調した変調波の電圧を、図2の復調回路に入力して復調したい。
コンデンサ\(C [F]\)と抵抗\(R [Ω]\)を並列接続した合成インピーダンスの両端電圧に求められることは、信号波の成分が\(\fbox{ (ア) }\)ことと、搬送波の成分が\(\fbox{ (イ) }\)ことである。
そこで、合成インピーダンスの大きさは、信号波の周波数に対してほぼ抵抗\(R [Ω]\)となり、搬送波の周波数に対して十分に \(\fbox{ (ウ) }\) なくてはならない。
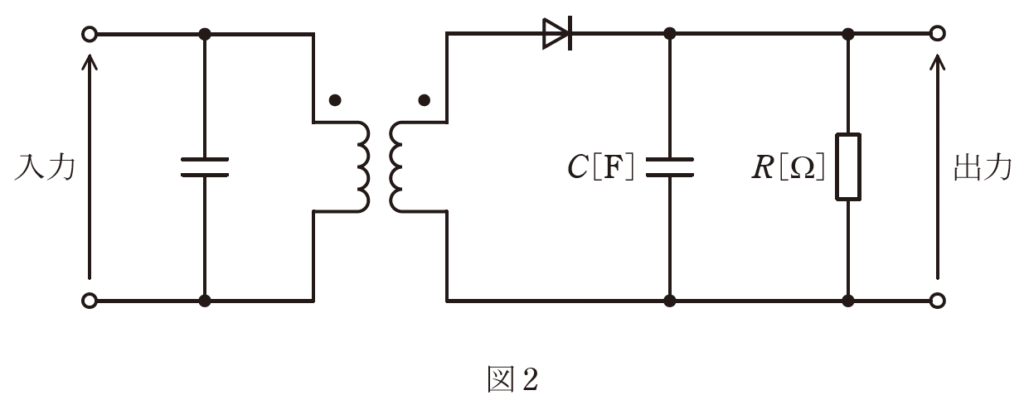
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
|---|---|---|---|
| (1) | ある | なくなる | 大きく |
| (2) | ある | なくなる | 小さく |
| (3) | なくなる | ある | 小さく |
| (4) | なくなる | なくなる | 小さく |
| (5) | なくなる | ある | 大きく |
答え
(a)(2)
(b)(2)
解説テキスト リンク
回答解説
(a)の解答の流れ
①変調波の振幅の最大・最小を読み取る
②変調度を計算する
①変調波の振幅の最大・最小を読み取る
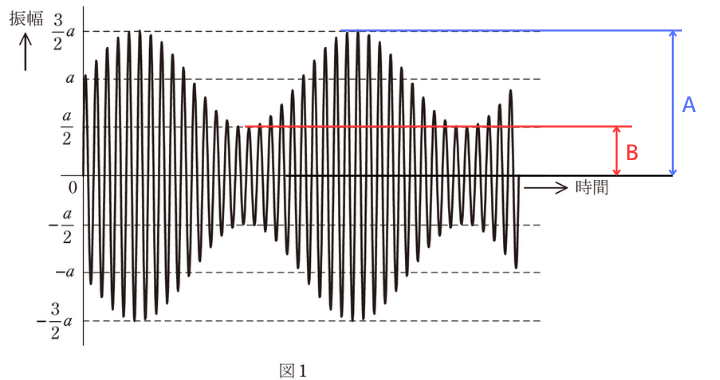
変調波の最大の振幅\(A\)は、
\(\displaystyle A=\frac{3}{2}a\)
変調波の最小の振幅\(B\)は、
\(\displaystyle B=\frac{1}{2}a\)
②変調度を計算する
変調度\(m\)の式は、
\(\displaystyle \begin{eqnarray}
m&=&\frac{A-B}{A+B} \\ \\
&=&\frac{\frac{3}{2}a-\frac{1}{2}a}{\frac{3}{2}a+\frac{1}{2}a} \\ \\
&=&\frac{a}{2a} \\ \\
&=&\frac{1}{2}
\end{eqnarray}\)
以上より、(a)問題の答えは(2)0.5 です。
(b)の解答
【信号波】
音声、映像等々の、送りたい情報の波です。
すなわち、受信機で受け取りたい信号であるため、復調回路の出力端子に信号波が(ア)あることが求められます。
【搬送波】
送信機・受信機間を電波としてつなげる高周波の波です。
搬送波は、特定の周波数のsin波で作られていて、信号波の情報を乗せるために使用されます。
受信機に到達した時点で役目を終えるため、復調回路の出力端子に搬送波が(イ)なくなることが求められます。
【出力端子の合成インピーダンスの大きさ】
合成インピーダンスの大きさは、信号波の周波数に対してほぼ抵抗\(R [Ω]\)となり、搬送波の周波数に対して十分に(ウ)小さくなくてはならない。
信号波は周波数が低い波です。搬送波は周波数が高い波です。
コンデンサ\(C[F]\)は、低周波に対してはインピーダンスが高く、高周波に対してはインピーダンスが低いです。そのため、検波回路はローパスフィルタとして働きます。
以上より、(b)問題の答えは(2)(ア)ある、(イ)なくなる、(ウ)小さく が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和5年度上期 第三種電気主任技術者試験 理論科目A問題問18
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント