難易度
クーロン力に関する難問です。
基本的な事を知っていれば二択までは持っていけます。
最後の二択は少々手間な式変形をする必要があります。
問題文中に式変形のヒントは与えられていますが、それを上手く使わないと回答は導き出せません。
上手く導き出せない時は、時間に追われず冷静に解く必要があるので、一度後回しにした方が良いかもしれません。
問題
次の文章は、帯電した導体球に関する記述である。
真空中で導体球A及びBが軽い絶縁体の糸で固定点Oからつり下げられている。真空の誘電率を\(ε_0[F/m]\)、重力加速度を\(g[m/s^2]\)とする。
A及びBは同じ大きさと質量\(m[kg]\)をもつ。
糸の長さは各導体球の中心点が点Oから距離\(l[m]\)となる長さである。
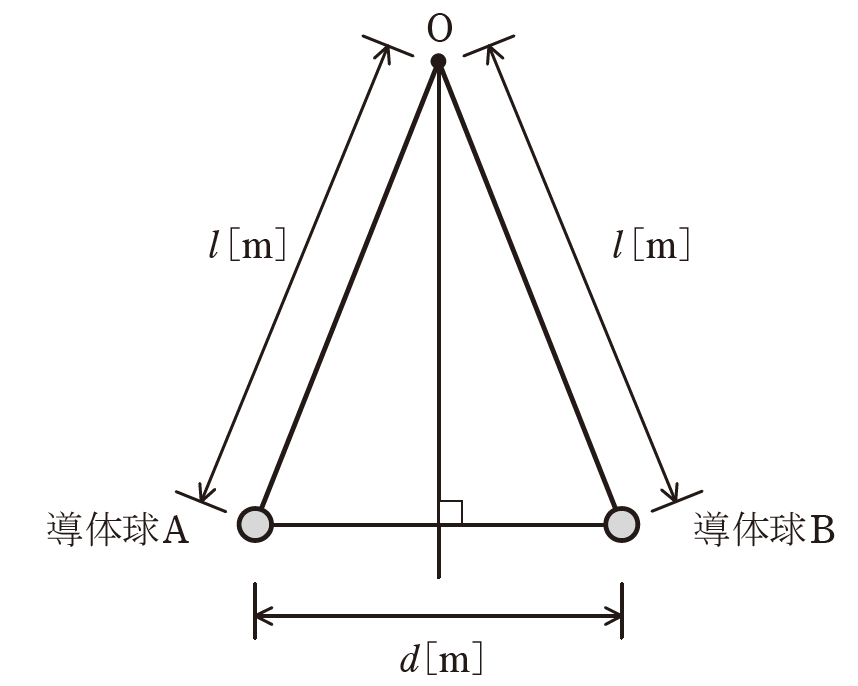
まず、導体球A及びBにそれぞれ電荷\(Q[C]\)、\(3Q[C]\)を与えて帯電させたところ、静電力による ア が生じ、図のようにA及びBの\(d[m]\)離れた状態で釣り合った。ただし、導体球の直径は\(d\)に比べて十分に小さいとする。
このとき、個々の導体球において、静電力\(F=\)イ \([N]\)、重力\(mg[N]\)、糸の張力\(T[N]\)、の三つの力が釣り合っている。三平方の定理より\(F^2+(mg)^2=T^2\)が成り立ち、張力の方向を考えると\(\displaystyle \frac{F}{T}\)は\(\displaystyle \frac{d}{2l}\)に等しい。
これらにより\(T\)を消去し整理すると、\(d\)が満たす式として、
\(\displaystyle k\left( \frac{d}{2l}\right)^3 = \sqrt{1-\left( \frac{d}{2l}\right)^2}\)
が導かれる。ただし、係数\(k=\)ウである。
次に、AとBとを一旦接触させたところAB間で電荷が異動し、同電位となった。そしてAとBとが力の釣合いの位置に戻った。接触前に比べ、距離\(d\)はエした。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 反発力 | \(\displaystyle \frac{3Q^2}{4\pi ε_0d^2}\) | \(\displaystyle \frac{16\pi ε_0l^2mg}{3Q^2}\) | 増加 |
| (2) | 吸引力 | \(\displaystyle \frac{Q^2}{4\pi ε_0d^2}\) | \(\displaystyle \frac{4\pi ε_0l^2mg}{Q^2}\) | 増加 |
| (3) | 反発力 | \(\displaystyle \frac{3Q^2}{4\pi ε_0d^2}\) | \(\displaystyle \frac{4\pi ε_0l^2mg}{Q^2}\) | 増加 |
| (4) | 反発力 | \(\displaystyle \frac{Q^2}{4\pi ε_0d^2}\) | \(\displaystyle \frac{16\pi ε_0l^2mg}{3Q^2}\) | 減少 |
| (5) | 吸引力 | \(\displaystyle \frac{Q^2}{4\pi ε_0d^2}\) | \(\displaystyle \frac{4\pi ε_0l^2mg}{Q^2}\) | 減少 |
答え
(1)
要点整理
クーロン力について

クーロン力は、正電荷-正電荷や、負電荷-負電荷の間では、互いに反発力が働きます。
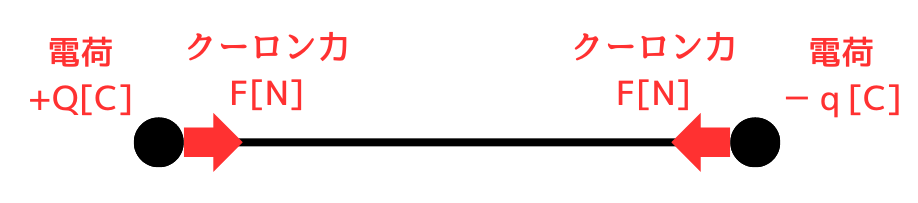
正電荷-負電荷の互いに符号が違う電荷間では引力が働きます。
二つの電荷間に働くクーロン力の大きさを求めます。
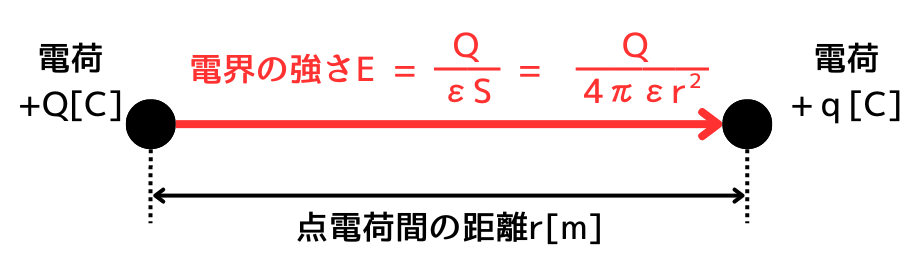
まず初めに、電荷\(+Q[C]\)が作り出す電界の強さ\(E[V/m]\)を求めます。
\(\displaystyle E=\frac{Q}{ε_0S}\)
です。
面積\(S\)は、球の表面積\(S=4πr^2\)なので、
\(\displaystyle E=\frac{Q}{4πε_0r^2}\)
と求まります。
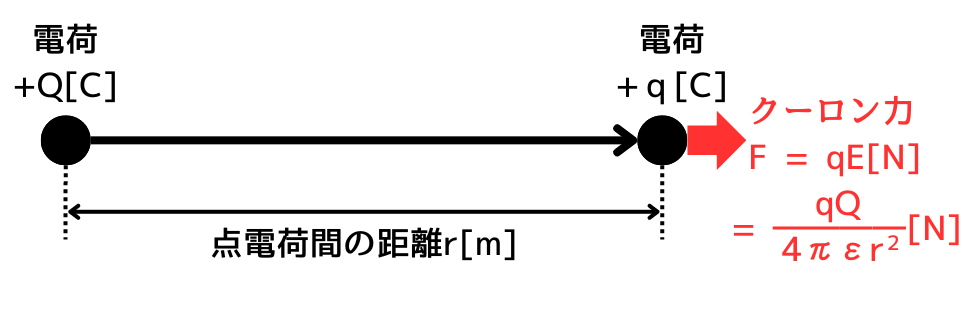
次に、電荷\(+Q[C]\)が作り出した電界\(E\)の中にある電荷\(q[C]\)に働くクーロン力\(F[N]\)は、
\(\displaystyle F=qE=\frac{qQ}{4πε_0r^2}\)
と求まります。
導体球にかかる力の向き
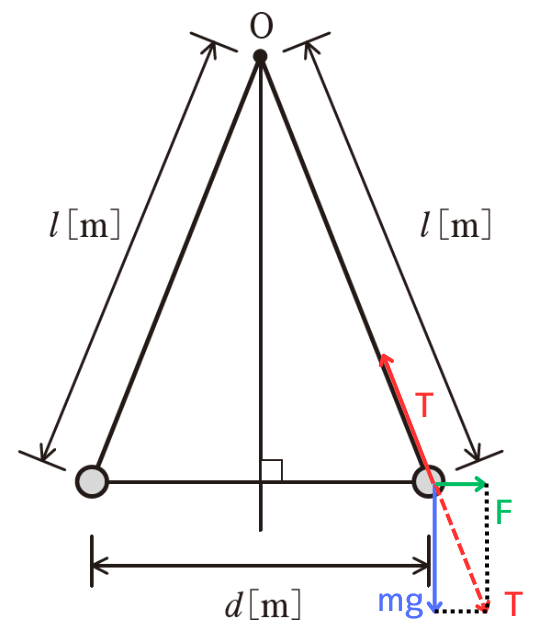
導体球にかかる力の向きは、図に示した通りです。
図の三角形のうち、クーロン力\(F[N]\)は\(\frac{d}{2}[m]\)に対応し、糸の張力\(T[N]\)は\(l[m]\)に対応します。
そのため、
\(\displaystyle \frac{F}{T}=\frac{\frac{d}{2}}{l}=\frac{d}{2l}\)
となります。
要点整理の適用
ア
二つの球に正電荷を帯電させたため、反発力が発生します。
イ
要点整理で示した通り、
\(\displaystyle F=3Q・E=\frac{3Q^2}{4πε_0d^2}\) ………①
のクーロン力が働きます。
ウ
問題文中で下記②③式が与えられています。
\(F^2+(mg)^2=T^2\) ………②
\(\displaystyle \frac{F}{T}=\frac{d}{2l}\) ………③
③式を変形した式も用意しておきます。
\(\displaystyle \frac{1}{T}=\frac{1}{F}\frac{d}{2l}\) ………④
②式を\(T^2\)で割った後、③・④式を代入します。
\(\displaystyle \left( \frac{F}{T} \right)^2+\left( \frac{mg}{T} \right)^2=1\)
⇔\(\displaystyle \left( \frac{d}{2l} \right)^2+\left( \frac{mg}{F}\frac{d}{2l} \right)^2=1\)
⇔\(\displaystyle \left( \frac{mg}{F}\frac{d}{2l} \right)^2=1-\left( \frac{d}{2l} \right)^2\)
⇔\(\displaystyle \frac{mg}{F}\frac{d}{2l} =\sqrt{1-\left( \frac{d}{2l} \right)^2}\) ……⑤
⑤式に、①式を代入します。
\(\displaystyle \frac{4πε_0d^2mg}{3Q^2}\frac{d}{2l} =\sqrt{1-\left( \frac{d}{2l} \right)^2}\)
⇔\(\displaystyle \frac{16πε_0l^2mg}{3Q^2} \left( \frac{d}{2l} \right)^3 =\sqrt{1-\left( \frac{d}{2l} \right)^2}\) ………⑥
⇔\(\displaystyle k \left( \frac{d}{2l} \right)^3 =\sqrt{1-\left( \frac{d}{2l} \right)^2}\) ………⑦
以上、⑥⑦より、
\(\displaystyle k=\frac{16πε_0l^2mg}{3Q^2}\)
エ
導体球を接触させると、導体球Bから導体球Aに電荷が移動し、両方の電荷は等しくなるので、それぞれの電荷は\(2Q[C]\)となります。
AB間の距離が\(d'[m]\)とすると、
\(\displaystyle F=\frac{4Q^2}{4πε_0d’^2}=\frac{Q^2}{πε_0d’^2}\) ……⑧
導体球を接触させる前の式①と、後の式⑧を比較すると
\(\displaystyle \frac{3Q^2}{4πε_0d^2}=\frac{4Q^2}{4πε_0d’^2}=\frac{Q^2}{πε_0d’^2}\)
⇔\(d’=\sqrt{\frac{4}{3}}d\)
以上より、\(d’\)は\(d\)よりも増加しました。
以上より、答えは(1)です。
出典元
令和5年度第三種電気主任技術者試験 理論科目A問題下期問2
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント