難易度
ソース接地の小信号増幅回路の問題です。
問題としては難しくはないですが、増幅回路の重要な要素が色々詰まっているのでしっかり勉強する価値はある問題です。
問題
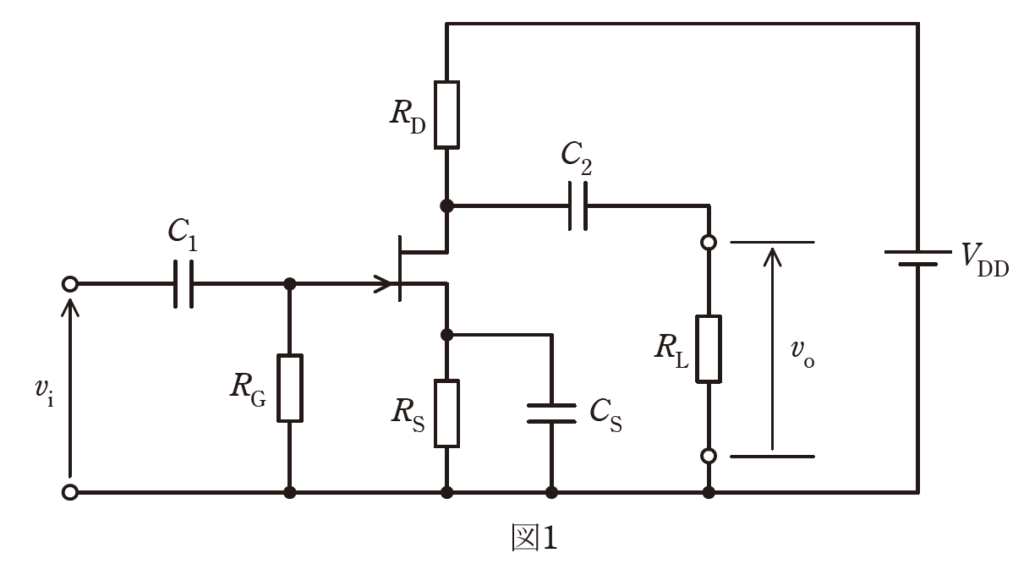
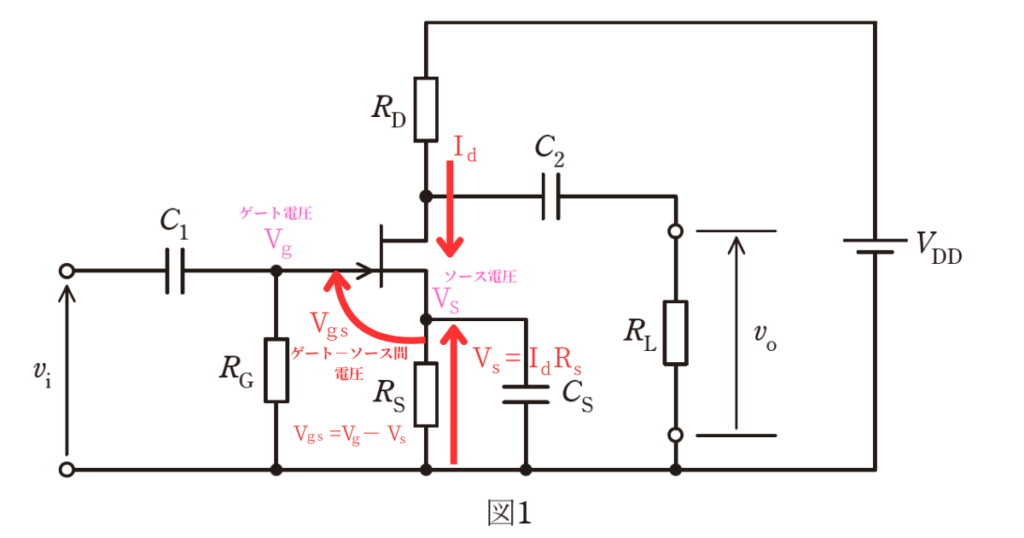
図1は、飽和領域で動作する接合形FETを用いた増幅回路を示し、図中の\(v_i\)並びに\(v_o\)はそれぞれ、入力と出力の小信号交流電圧[V]を表す。また、図2は、その増幅回路で使用するFETのゲート-ソース間電圧\(V_{gs}[V]\)に対するドレーン電流\(I_d[mA]\)の特性を示している。抵抗\(R_G=1MΩ\)、\(R_D=5kΩ\)、\(R_L=2.5kΩ\)、直流電源電圧\(V_{DD}=20V\)とするとき、次の(a)及び(b)の問に答えよ。
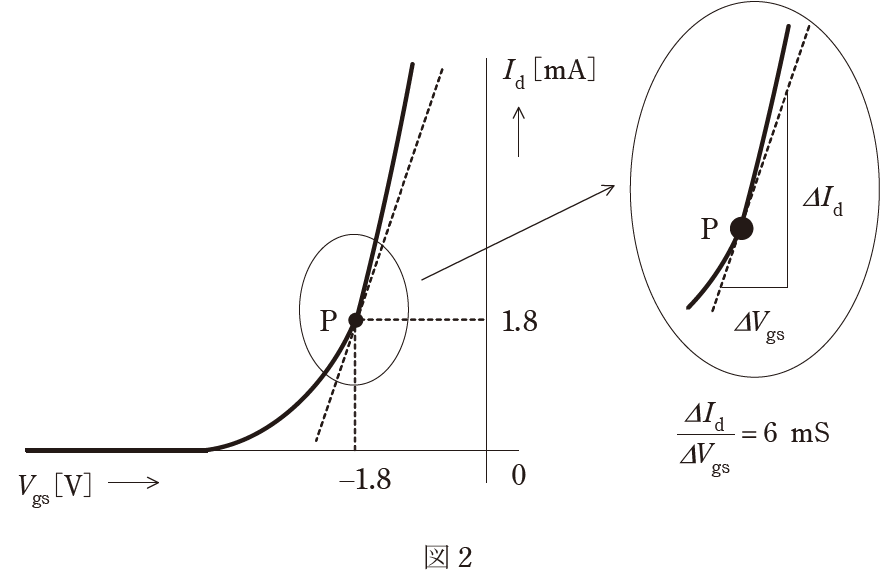
(a) FET の動作点が図2の点Pとなる抵抗\(R_S\)の値\([kΩ]\)として、最も近いものを
次の(1)~(5)のうちから一つ選べ。
(1) 0.1 (2) 0.3 (3) 0.5 (4) 1 (5) 3
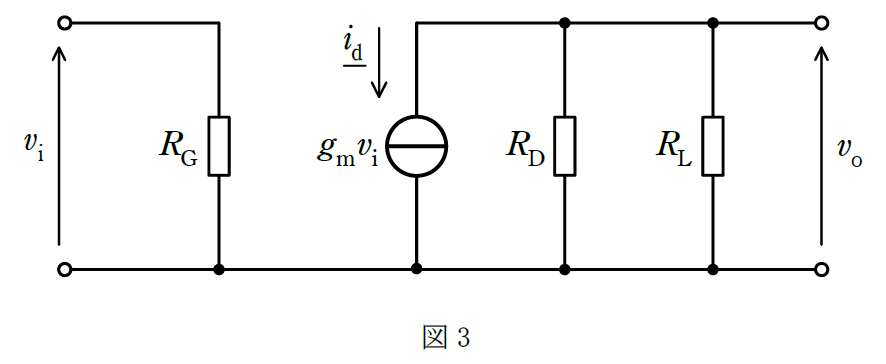
(b) 図2の特性曲線の点P における接線の傾きを読むことで、FET の相互コンダクタンスが\(g_m=6mS\)であるとわかる。この値を用いて、増幅回路の小信号交流等価回路をかくと図3となる。
ここで、コンデンサ\(C_1\)、\(C_2\)、\(C_S\)のインピーダンスが使用する周波数で十分に小さいときを考えており、FET の出力インピーダンスが\(R_D[kΩ]\)や\(R_L[kΩ]\)より十分大きいとしている。
この増幅回路の電圧増幅度\(\displaystyle A_v=\left| \frac{v_o}{v_i} \right| \)の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 10 (2) 30 (3) 50 (4) 100 (5) 300
答え
(a) (4)
(b) (1)
要点整理
ソース接地回路
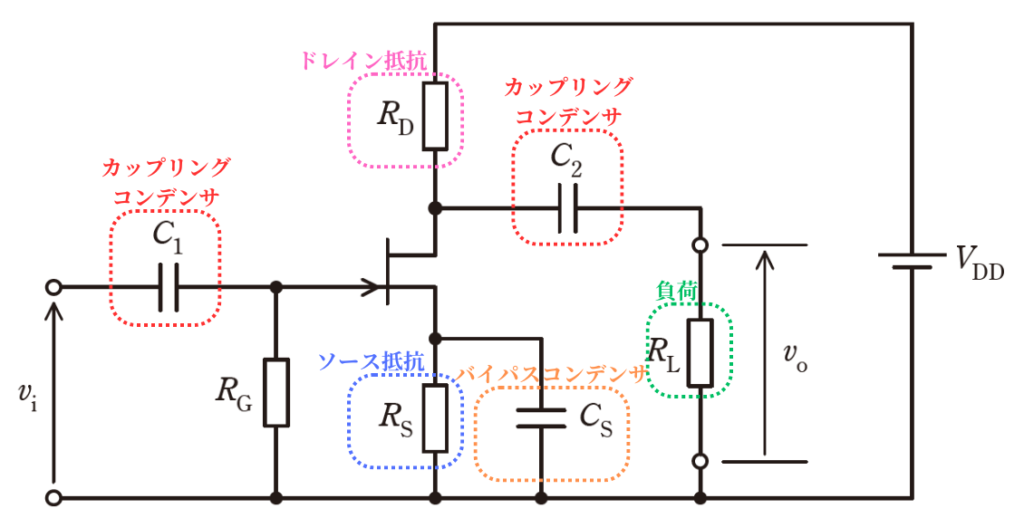
トランジスタ回路には、ソース接地、ゲート接地、ドレイン接地(ソースフォロワ)の3種類があります。
その中でもソース接地回路は、信号を増幅するのに最も適した回路です。
主な特徴は、
・電圧増幅率が高い
・入力信号と出力信号が反転する
・出力インピーダンスが高い
です。
この特徴のうち、出力インピーダンスが高い点が大きな短所です。

その理由は、出力電圧信号は、左図の通り、
\(\displaystyle v_o=\frac{R_DR_L}{R_D+R_L}g_mv_i\)
となります。
そのため、スピーカーの様な低インピーダンスの負荷が\(R_L\)に接続されると、電圧が増幅されなくなります。
本問の出題の条件だと、
・FET の相互コンダクタンス\(g_m=6mS\)
・ドレイン抵抗\(R_D=5[kΩ]\)
・負荷抵抗\(R_L=2.5[kΩ]\)
この時の増幅回路の電圧増幅度\(\displaystyle A_v=\left| \frac{v_o}{v_i} \right| \)は、
\(\displaystyle A_v=\frac{5000・2500}{5000+2500}・0.006=10倍\)です。
次に、負荷抵抗\(R_L\)をスピーカーの様な低インピーダンスの負荷として計算してみます。
・FET の相互コンダクタンス\(g_m=6mS\)
・ドレイン抵抗\(R_D=5[kΩ]\)
・負荷抵抗\(R_L=8[Ω]\)
この時の増幅回路の電圧増幅度\(\displaystyle A_v=\left| \frac{v_o}{v_i} \right| \)は、
\(\displaystyle A_v=\frac{R_DR_L}{R_D+R_L}g_m=\frac{5000・8}{5000+8}・0.006=0.048倍\)です。
したがって、低インピーダンスの負荷を接続した時、信号を増幅するどころか大幅に減衰してしまいました。
この2つの負荷条件による電圧増幅度の計算結果から、接続する負荷によって電圧増幅度が大きく異なってしまうことがわかります。
この問題を解決するためには、ソース接地回路の出力に、ドレイン接地回路(ソースフォロワ)のように出力インピーダンスが低い回路を接続してその出力を負荷に接続することで解決できます。
カップリングコンデンサ
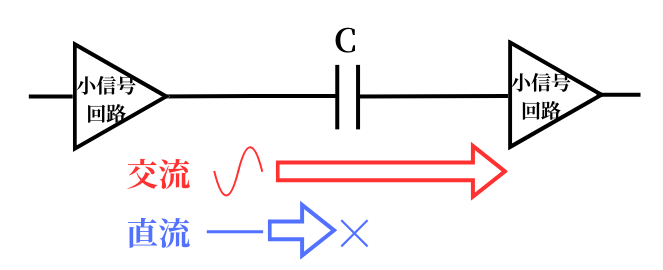
カップリングコンデンサとは、直流成分をコンデンサで遮断し、交流成分のみを通過させるコンデンサです。
小信号回路と小信号回路を結合するために使用されるので、カップリング(結合)コンデンサと名前がついています。
増幅回路のような小信号回路の動作条件はトランジスタによって異なります。
そのため、【直流成分+交流成分】となった状態で、後段の小信号回路に信号を送ると、動作に影響を与えることがあります。
そのため、カップリングコンデンサで結合することで、交流信号のみを送ることができるようになります。
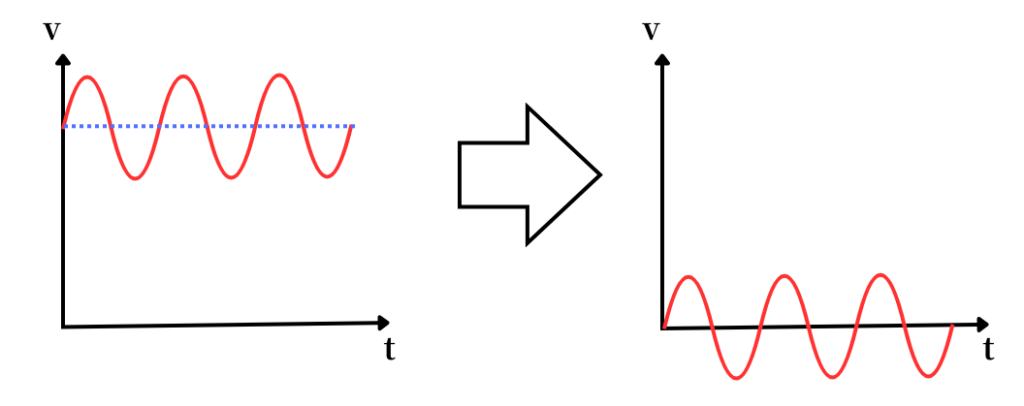
左図の左側の波形イメージは、直流成分+交流成分の波形です。
カップリングコンデンサを通すことによって、直流成分が取り除かれ、交流成分だけとなった波形が右側の波形イメージです。
デカップリングコンデンサ
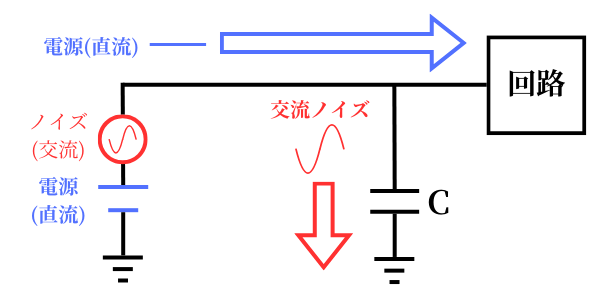
電源にノイズが乗ってしまうと、電源電圧が変動するため、回路が予定していない動作をしてしまう可能性があります。
その対策として、デカップリングコンデンサを使用して、電源ラインに乗ってしまったノイズを除去をします。
デカップリングコンデンサは、コンデンサの交流成分のみを通過させる特性を利用するコンデンサの使い方です。
直流成分は回路の電源として送り出し、交流成分(ノイズ)は、デカップリングコンデンサを通してグラウンドに逃がします。
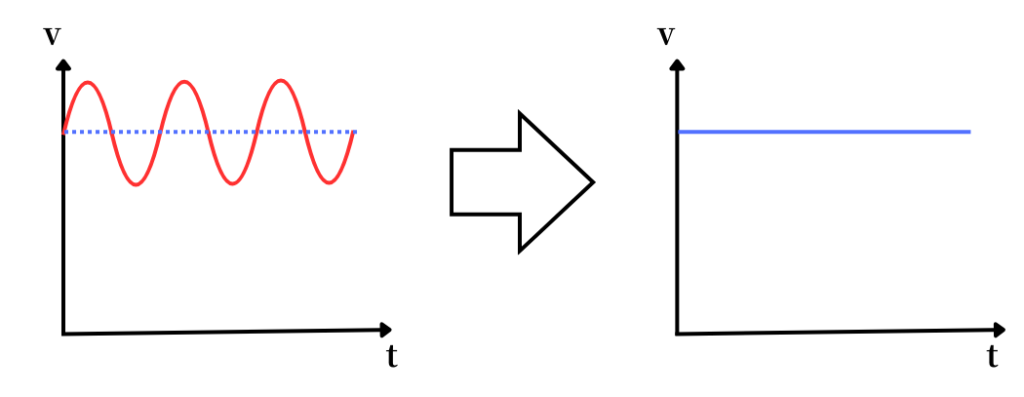
左図の左側の波形イメージは、直流成分+交流成分の波形です。
デカップリングコンデンサを通すことによって、交流成分が取り除かれ、直流成分だけとなった波形が右側の波形イメージです。
デカップリングコンデンサは、コンデンサの容量によって周波数特性が異なります。
そのため、低減したいノイズの周波数に合わせて容量を選定する必要があります。
シビアなアナログ回路設計をする場合は、同じ静電容量のコンデンサを並列接続することで、インピーダンスを下げることを検討することもあります。
ソース抵抗(デジェネレーション抵抗)

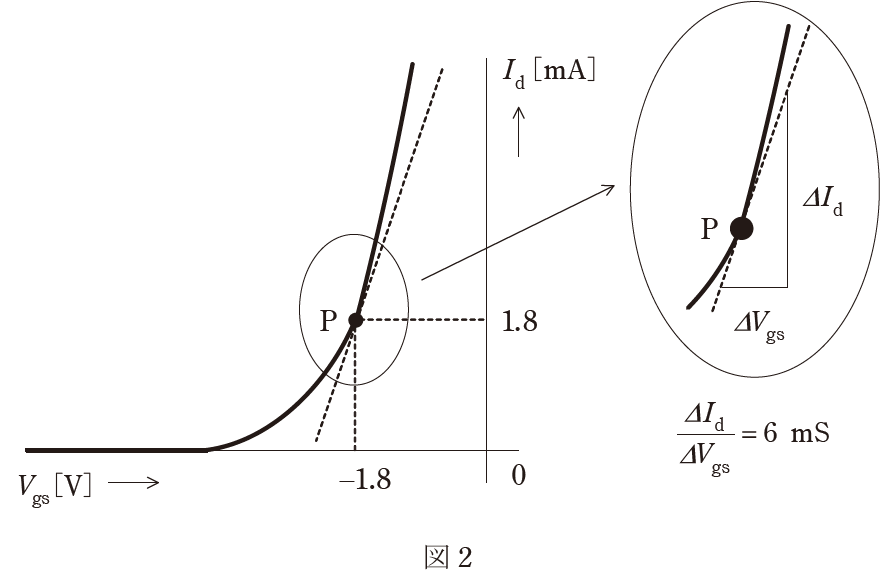
FETのソース接地の小信号増幅回路は、\(V_{gs}-I_d\)特性のグラフからわかる通り、入力信号\(V_{gs}\)が変動すると、ドレイン電流\(I_d\)は非線形に変動します。
出力電圧\(v_o\)は、
\(v_o=(R_D//R_L)・I_d\)
となりますので、出力信号はドレイン電流\(I_d\)に依存します。
つまり、ドレイン電流\(I_d\)が非線形に変動すれば、出力電圧\(v_o\)も非線形に変動します。
そのため、出力電圧は歪んでしまいます。
その対策として、FETのソース端子にソース抵抗\(R_S\)を接続することで、その歪みを小さくすることができます。
しかし、その副作用として、トランスコンダクタンスが低下する(=電圧増幅率が低下する)ため、デジェネレーション(退化)抵抗と呼ばれます。
デジェネレーション抵抗の動作について説明します。
①ドレイン電流\(I_d\)が増加する。
②ソース抵抗\(R_s\)の端子電圧\(V_s=R_sI_d\)が増加する。
③\(V_{gs}=V_g-V_s\)なので、\(V_s\)が増加すると、\(V_{gs}\)が減少する。
④\(V_{gs}\)が減少すると、ドレイン電流\(I_d\)が減少する。
このようにフィードバック動作を繰り返しながら動くため、ドレイン電流\(I_d\)の変化は小さくなります。したがって、トランスコンダクタンス\(g_m\)は小さくなります。
回路の電圧増幅率\(A_v\)は、\(A_v=g_mR\)なので、トランスコンダクタンスが小さくなると電圧増幅率も低下しますが、線形性が高くなります。
バイパスコンデンサ

ソース抵抗\(R_s\)を接続すると、ソース端子の電圧が、\(V_s=R_s・I_d\)の分だけ上昇します。
そうなると、ソース抵抗の分だけ、出力端子の電圧\(v_o\)の上下に変動できる範囲が狭くなります。
FETのソース端子に接続されたソース抵抗\(R_s\)と並列に、バイパスコンデンサ\(C_s\)を接続することで、交流的には抵抗\(R_s\)が無いように取り扱うことができます。
このような目的で使用されるコンデンサのことをバイパスコンデンサと言います。コンデンサは交流信号は素通りさせて直流信号は遮断する特性があるので、バイパスコンデンサを入れてもソース抵抗の直流動作には影響を与えません。
回答解説
問(a)
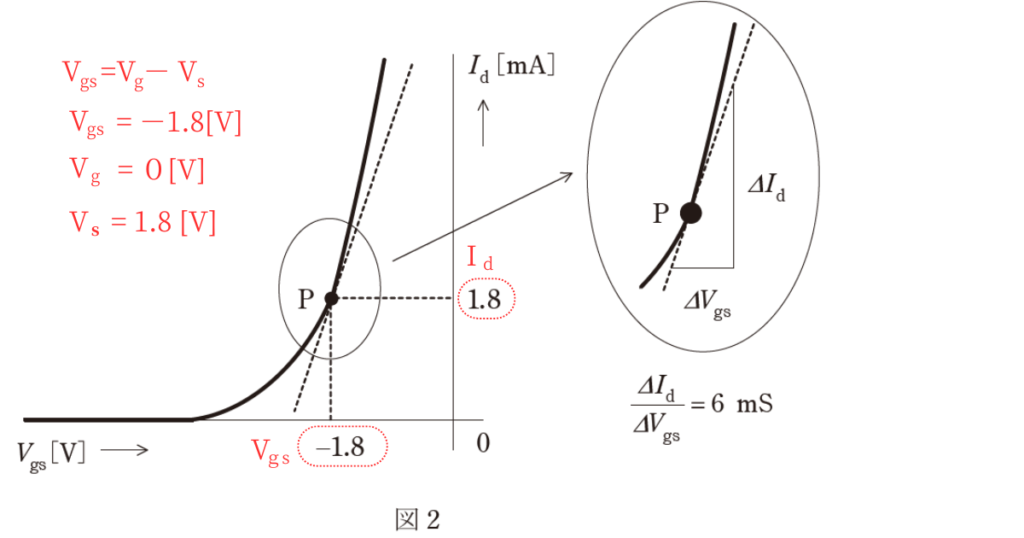
ゲート-ソース間電圧は図2のグラフから
\(V_{gs}=-1.8[V]\) ………①
入力信号は\(v_i\)からカップリングコンデンサ\(C_1\)を通ってからゲートに印加されるため、ゲート電圧の直流成分は
\(V_g=0[V]\) ………②
ゲートソース間電圧\(V_{gs}\)と、ゲート電圧\(V_g\)、ソース電圧\(V_s\)の関係は
\(V_{gs}=V_g-V_s\) ………③
です。③式を変形し、①②を代入すると、
ソース電圧\(V_s\)は、
\(\begin{eqnarray}
V_s&=&V_g-V_{gs}\\
&=&0-(-1.8)\\
&=&1.8[V] ………④
\end{eqnarray}\)
となります。
図2のグラフから、ドレイン電流\(I_d\)は、
\(I_d=1.8[mA]\) ………⑤
です。ドレイン電流はソース抵抗\(R_s\)に流れるので、ソース電圧\(V_s\)は、
\(V_s=R_sI_d\) ………⑥
⑥式に④・⑤を代入すると、
\(\displaystyle R_s=\frac{V_s}{I_d}=\frac{1.8}{1.8×10^{-3}}=1000[Ω]=1[kΩ]\)
以上より、ソース抵抗\(R_s[kΩ]\)は、(4)\(R_s=1[kΩ]\)です。
問(b)
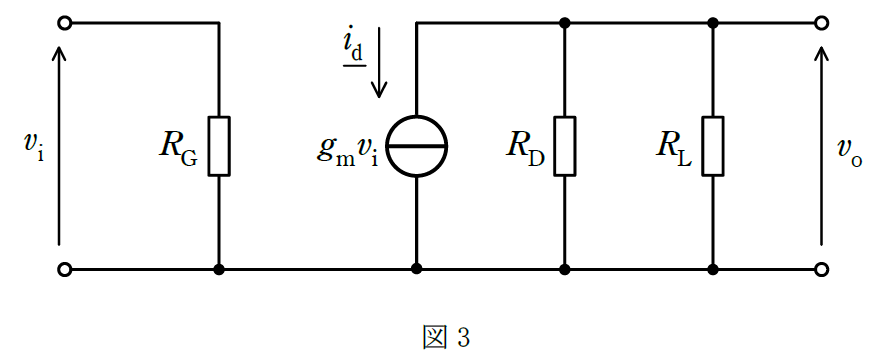
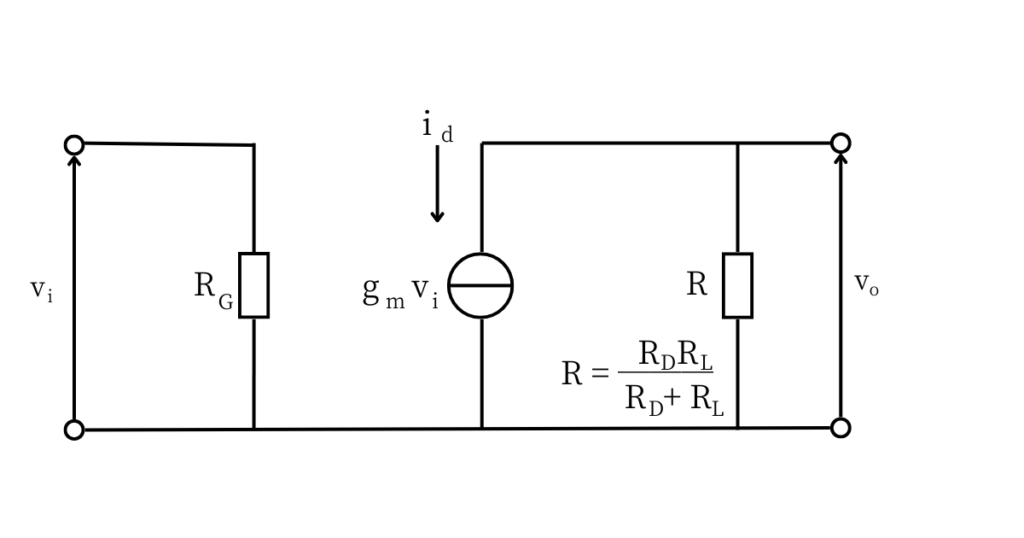
問題文中の図1の小信号等価回路は図3となります。
FETは、電圧制御電流源であり、入力電圧信号\(v_i\)で、ドレイン電流\(i_d\)の電流量を制御します。図3にある通り、
\(i_d=g_mv_i\) ………①
です。
FETの出力は、ドレイン抵抗\(R_D\)と、負荷抵抗\(R_L\)の両方に流れるので、並列に接続されたものとして扱われます。
\(R_D\)と\(R_L\)の合成抵抗を\(R[Ω]\)とすると、
\(\displaystyle R=\frac{R_DR_L}{R_D+R_L}\) ………②
合成抵抗\(R\)に流れる電流は\(i_d\)なので、出力電圧\(v_o\)は、
\(v_o=R i_d\) ………③
③式に①式を代入すると、
\(v_o=g_mRv_i\)
⇔\(\displaystyle A_v=\frac{v_o}{v_i}=g_mR\)
⇔\(\displaystyle A_v=g_m\frac{R_DR_L}{R_D+R_L}=6×10^{-3}・\frac{5×10^3・2.5×10^3}{5×10^3+2.5×10^3}=10\)
以上より、(1)電圧増幅度\(A_v=10\)です。
出典元
令和5年度第三種電気主任技術者試験 理論科目B問題下期問18
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント