難易度
環状鉄心の結合係数を求める問題です。
自己・相互インダクタンスに対する理解と、磁束の流れから和動・差動接続のどちらがされているかを把握して回答することが問われますので、少々難しい問題です。
キーワード
自己インダクタンス\(L[H]\)、相互インダクタンス\(M[H]\)、結合係数\(k\)
和動接続、差動接続
問題
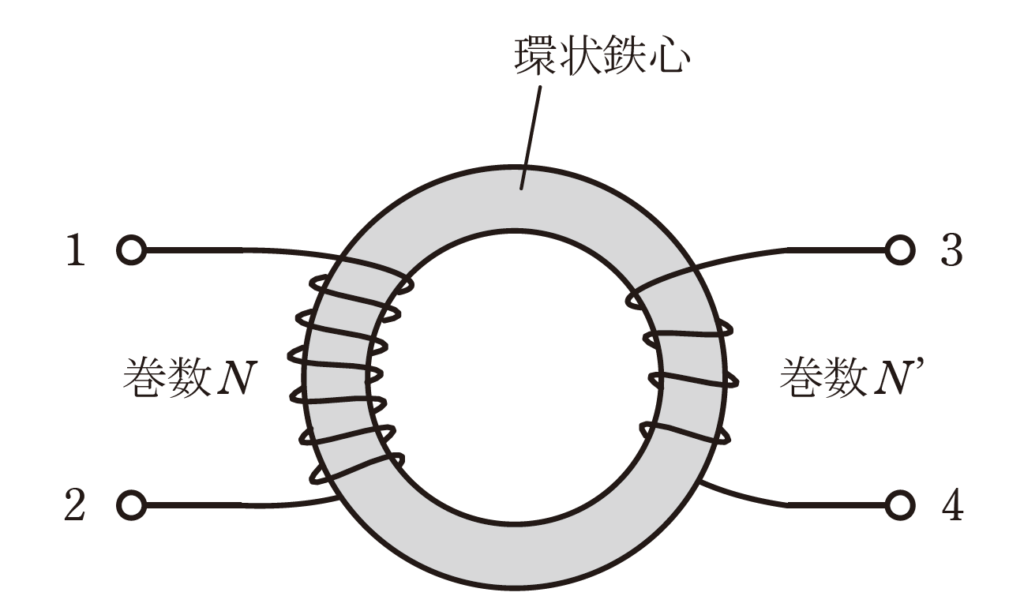
図のような環状鉄心に巻かれたコイルがある。
図の環状コイルについて、
・端子1-2 間の自己インダクタンスを測定したところ、\(40 mH\) であった。
・端子3-4 間の自己インダクタンスを測定したところ、\(10 mH\) であった。
・端子2 と3 を接続した状態で端子1-4 間のインダクタンスを測定したところ、\(86 mH\) であった。
このとき、端子1-2 間のコイルと端子3-4 間のコイルとの間の結合係数k の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.81 (2) 0.90 (3) 0.95 (4) 0.98 (5) 1.8
答え
(2)
要点整理
自己インダクタンス L ・相互インダクタンスM
インダクタンス\(L[H]\)
コイルに流れる電流が変化して誘導起電力が現れる場合、この誘導起電力と電流変化量との比例定数のことです。
つまり、電流変化に対する電磁誘導の大きさを表します。
自己インダクタンス\(L[H]\)
自己誘導作用におけるインダクタンスを示す場合、自己インダクタンス\(L\)と呼びます。
自己インダクタンス\(L\)と誘導起電力の関係は、次式で表すことができます。
\(\displaystyle e=-L\frac{di}{dt}\)
相互インダクタンス\(M\)
相互誘導作用におけるインダクタンスを示す場合、相互インダクタンス\(M\)と呼びます。相互インダクタンス\(M[H]\)と誘導起電力の関係は、次式で表すことができます。
\(\displaystyle e=-M\frac{di}{dt}\)
自己誘導作用・誘導起電力
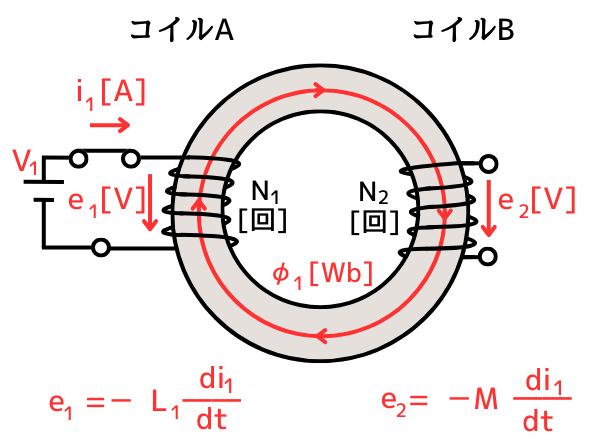
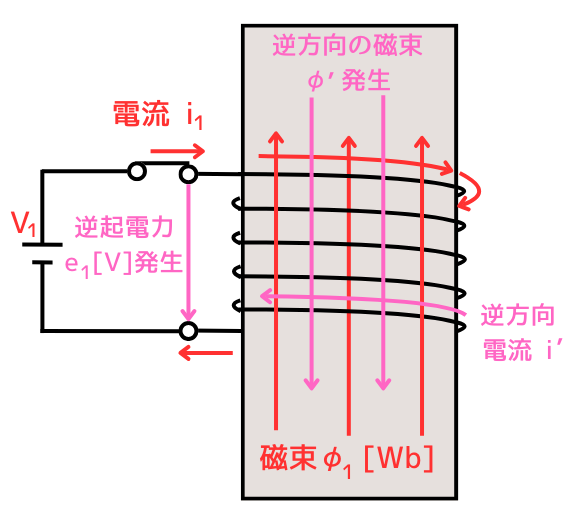
コイルAに電流\(i_1[A]\)を流すと、コイルA自身に流れる電流が磁束を作り出しますので、コイルの中を通過する磁束の量が変化します。
コイルAの中を通過する磁束の量が変化すると、ファラデーの電磁誘導の法則にしたがい、磁束の変化を妨げる向きに逆起電力が生じます。この逆起電力は、誘導起電力と呼ばれます。
そして、誘導起電力を生み出す作用のことを自己誘導作用と呼びます。
誘導起電力の大きさ①
コイルの巻数が\(N_1\)[回]の時、コイルAに電流が流れた時に\(N_1\)本のコイルの線の一本一本が、それぞれ磁束\(\phi_1\)を発生させます。
そのため、磁束の変化\(\frac{d\phi_1}{dt}\)を妨げる向きに発生する誘導起電力は、
\(\displaystyle e_1=-N_1\frac{d\phi_1}{dt}\) ………①
となります。
・\(e_1[V]\):コイルAに発生する誘導起電力(逆起電力)
・\(N_1\)[回]:コイルAの巻数
・\(\phi_1[Wb]\):コイルAが作る磁束
・\(\frac{d\phi_1}{dt}\):コイルAが作る磁束の変化量
誘導起電力の大きさ②
電流\(i_1\)が変化した時の、電流の変化量は\(\frac{di_1}{dt}\)です。
誘導起電力は、その電流の変化量にも比例して大きくなります。
誘導起電力-電流の変化量間の比例定数を、インダクタンス\(L[H]\)と呼びます。
電流が流れたコイルA自身が生み出す誘導起電力\(e_1\)と、電流の変化量\(\frac{di_1}{dt}\)の間の比例定数は、自己インダクタンス\(L\)と呼びます。この関係を式に表すと、
\(\displaystyle e_1=-L_1\frac{di_1}{dt}\) ………②
となります。
・\(e_1[V]\):コイルAに発生する誘導起電力(逆起電力)
・\(L_1[H]\):コイルAの自己インダクタンス
・\(i_1[A]\):コイルAに流れる電流
・\(\frac{di_1}{dt}\):コイルAに流れる電流の変化量
誘導起電力の大きさ③
電流が流れたコイルAが磁束を生み出し、鉄心中を流れてコイルBを通過するときに、コイルBに発生する逆起電力と、コイルAに流れる電流の変化量の間の比例定数は、相互インダクタンス\(M\)と呼びます。この関係を式に表すと、
\(\displaystyle e_2=-M\frac{di_1}{dt}\) ………③
・\(e_2[V]\):コイルBに発生する誘導起電力(逆起電力)
・\(M[H]\):コイルA-コイルB間の相互インダクタンス
・\(i_1[A]\):コイルAに流れる電流
・\(\frac{di_1}{dt}\):コイルAに流れる電流の変化量
結合係数k
結合係数\(k\)は、鉄心に巻かれた2つのコイル間の結合度合いを示す係数です。
結合係数\(k\)は、次の式で示されます。
\(\displaystyle k=\frac{M}{\sqrt{L_1L_2}}\)
数字の範囲は、\(k=0~1\)です。
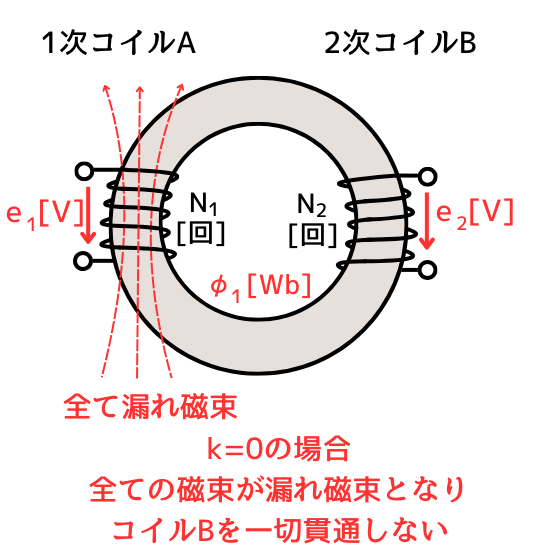
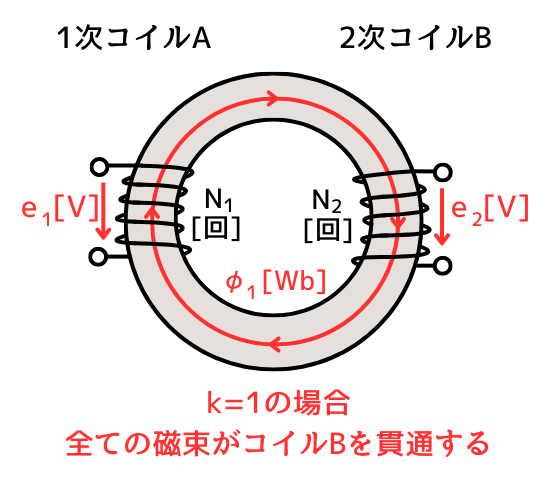
結合係数\(k\)は、片方のコイルが作った磁束が、他方のコイルを貫く割合を表したものです。
\(k\)が小さいと、漏れ磁束が多くなり他方のコイルを貫く割合は小さくなります。
\(k=0\)の場合、片方のコイルが作った磁束は、全て漏れ磁束となるため、他方のコイルを一切貫きません。
\(k=1\)の場合、片方のコイルが作った磁束は、全て他方のコイルを貫きます。
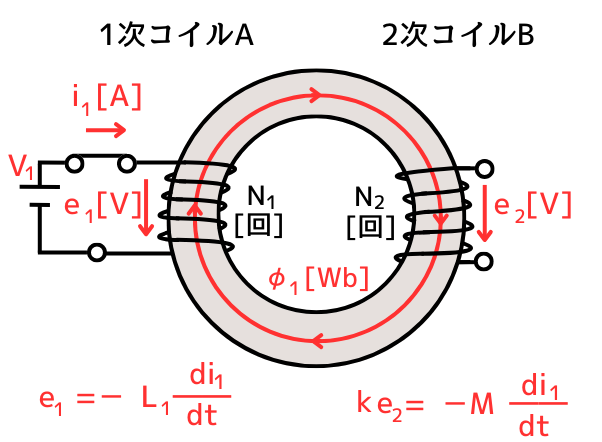
結合係数\(k\)の式を導出します。
一次回路に電流変化を与えたときの自己誘導および相互誘導の関係式は
\(\displaystyle \begin{eqnarray}
\left\{
\begin{array}{l}
e_1=-L_1 \frac{di_1}{dt} ………①\\
ke_2=-M \frac{di_1}{dt} ………②
\end{array} \right.
\end{eqnarray}\)
※②式は、結合係数によって誘導起電力\(e_2\)が変化するので、\(ke_2\)として表しています。
②÷①をすると、
\(\displaystyle k\frac{e_2}{e_1}=\frac{M}{L_1}\)
⇔\(\displaystyle \frac{e_2}{e_1}=\frac{M}{kL_1}\) ………③
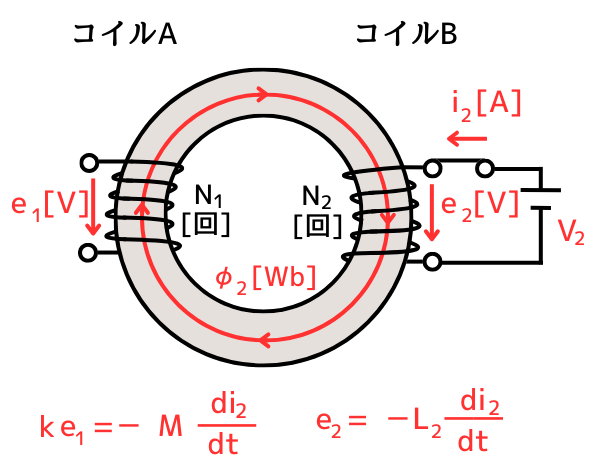
二次回路に電流変化を与えたときの自己誘導および相互誘導の関係式は
\(\displaystyle \begin{eqnarray}
\left\{\begin{array}{l}
ke_1=-M \frac{di_2}{dt} ………④\\
e_2=-L_2 \frac{di_2}{dt} ………⑤
\end{array} \right.
\end{eqnarray}\)
※④式は、結合係数によって誘導起電力\(e_1\)が変化するので、\(ke_1\)として表しています。
④÷⑤をすると、
\(\displaystyle k\frac{e_1}{e_2}=\frac{M}{L_2}\)
⇔\(\displaystyle \frac{e_1}{e_2}=\frac{M}{kL_2}\) ………⑥
③・⑥式から
\(\displaystyle \frac{M}{kL_1}=\frac{kL_2}{M}\)
⇔\(M^2=k^2L_1L_2\)
⇔\(M=k\sqrt{L_1L_2}\)
⇔\(\displaystyle k=\frac{M}{\sqrt{L_1L_2}}\)
和動接続
1次コイルAと、2次コイルBを接続する方法には2つあります。
①和動接続:磁束が発生する方向を合わせて接続する方法
②差動接続:磁束が発生する方向が逆向きになるように接続する方法
和動接続の時
合成された自己インダクタンス\(L\)は、コイルAの自己インダクタンスを\(L_1\)、コイルBの自己インダクタンスを\(L_2\)、相互インダクタンスを\(M\)とするとき、次式で表されます。
\(L=L_1+L_2+2M\)
差動接続の時
合成された自己インダクタンス\(L\)は、コイルAの自己インダクタンスを\(L_1\)、コイルBの自己インダクタンスを\(L_2\)、相互インダクタンスを\(M\)とするとき、次式で表されます。
\(L=L_1+L_2-2M\)
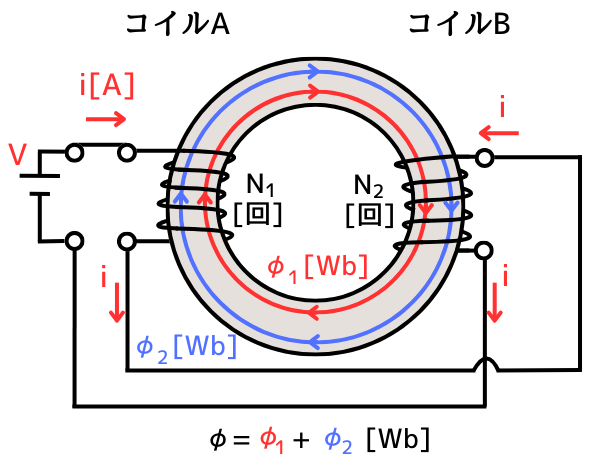
和動接続
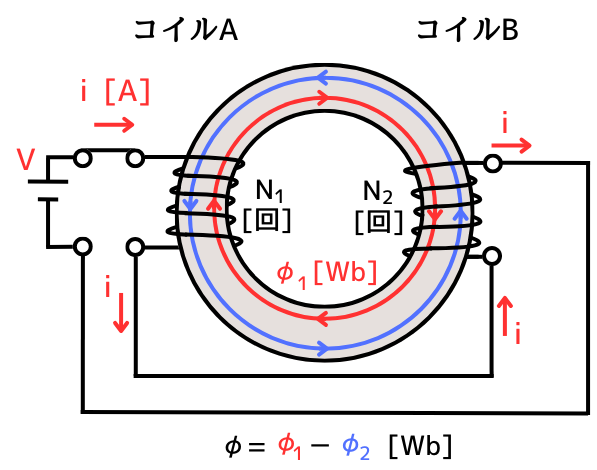
左図のように、コイルAに電流を流した時に発生する磁束\(\phi_1\)の方向と、コイルBに電流を流した時に発生する磁束\(\phi_2\)の方向を合わせるように、コイルAとコイルBを接続した時を和動接続と呼びます。
この時の合成インダクタンス\(L\)を求めます。
\(Li=N_1(\phi_1+\phi_2)+N_2(\phi_1+\phi_2)\)
⇔\(Li=N_1\phi_1+N_1\phi_2+N_2\phi_1+N_2\phi_2\)
⇔\(Li=L_1i+Mi+L_2i+Mi\)
⇔\(L=L_1+L_2+2M\)
差動接続
左図のように、コイルAに電流を流した時に発生する磁束\(\phi_1\)の方向と、コイルBに電流を流した時に発生する磁束\(\phi_2\)の方向が逆を向くように、コイルAとコイルBを接続した時を差動接続と呼びます。
この時の合成インダクタンス\(L\)を求めます。
\(Li=N_1(\phi_1-\phi_2)+N_2(\phi_1-\phi_2)\)
⇔\(Li=N_1\phi_1-N_1\phi_2+N_2\phi_1-N_2\phi_2\)
⇔\(Li=L_1i-Mi+L_2i-Mi\)
⇔\(L=L_1+L_2-2M\)
\(i[A]\):コイルに流れる電流
\(N_1\)[回]:コイルAの巻数
\(N_2\)[回]:コイルBの巻数
\(\phi_1[Wb]\):コイルAが作り出す磁束
\(\phi_2[Wb]\):コイルBが作り出す磁束
\(L_1[H]\):コイルAの自己インダクタンス
\(L_2[H]\):コイルBの自己インダクタンス
\(M[H]\):相互インダクタンス
回答解説

・端子1-2 間の自己インダクタンスが\(40 mH\) であることから、左側の巻数\(N\)のコイルの自己インダクタンス\(L_1[H]\)は、\(L_1=40mH\)です。
・端子3-4 間の自己インダクタンスが\(10 mH\) であることから、右側の巻数\(N’\)のコイルの自己インダクタンス\(L_2[H]\)は、\(L_2=10mH\)です。
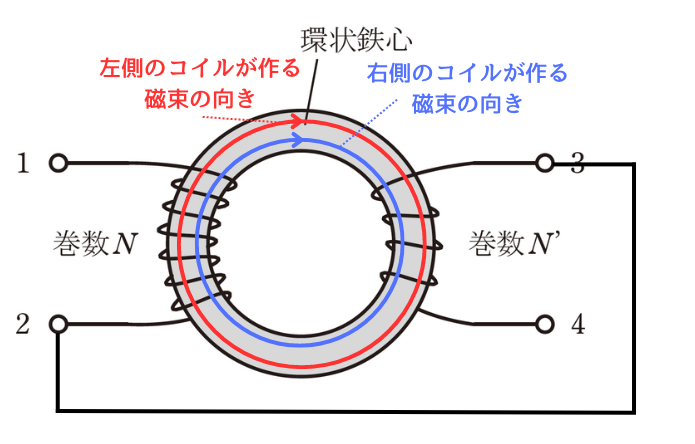
・端子2 と3 を接続した状態で端子1-4 間のインダクタンスを測定したところ、\(86 mH\) であったの記述について、検討します。
端子2と3を接続した状態で、端子1-4のインダクタンスを測定すると、左図のようになります。
コイルの巻いている向きと、電流の流れる向きから、右ねじの法則で、左側のコイルも、右側のコイルも時計回りに磁束を作ることがわかります。
したがって、図の回路は和動接続です。
和動接続の時に測定できるインダクタンス\(L\)、各自己インダクタンス\(L_1、L_2\)と、相互インダクタンス\(M\)の関係は、
\(L=L_1+L_2+2M\) ………①
なので、①式に測定結果をそれぞれ代入していきますと、相互インダクタンス\(M\)が求まります。
\(86=40+10+2M\)
⇔\(M=18[mH]\)
次に、自己インダクタンス、相互インダクタンスと、結合係数\(k\)の関係式
\(M=k\sqrt{L_1L_2}\) ………②
にそれぞれを代入していくと、
\(\displaystyle k=\frac{M}{\sqrt{L_1L_2}}=\frac{18}{\sqrt{40・10}}=\frac{18}{20}=0.9\)
以上より、答えは(2)の0.90と求まりました。
出典元
一般財団法人 電気技術者試験センター
令和4年度第三種電気主任技術者試験 理論科目A問題上期問3
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント