難易度
平行平板コンデンサの性質に関する問題で、少々ひねりが加えられているため、ある程度の理解が求められます。
問題
面積がともに\(S [m^2]\)で円形の二枚の電極板(導体平板)を、互いの中心が一致するように間隔\(d [m]\)で平行に向かい合わせて置いた平行板コンデンサがある。
電極板間は誘電率\(ε[F/m]\)の誘電体で一様に満たされ、電極板間の電位差は電圧\(V[V]\)の直流電源によって一定に保たれている。
この平行板コンデンサに関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、コンデンサの端効果は無視できるものとする。
(1) 誘電体内の等電位面は、電極板と誘電体の境界面に対して平行である。
(2) コンデンサに蓄えられる電荷量は、誘電率が大きいほど大きくなる。
(3) 誘電体内の電界の大きさは、誘電率が大きいほど小さくなる。
(4) 誘電体内の電束密度の大きさは、電極板の単位面積当たりの電荷量の大きさに等しい。
(5) 静電エネルギーは誘電体内に蓄えられ、電極板の面積を大きくすると静電エネルギーは増大する。
答え
(3)
要点整理
平行平板コンデンサの電界E[V/m]
平行平板コンデンサの電界\(E[V/m]\)の式
\(\displaystyle E=\frac{Q}{ε_rε_0S}\)
比誘電率\(ε_r\)、真空の誘電率\(ε_0[F/m]\)、極板面積\(S[m^2]\)は定数。
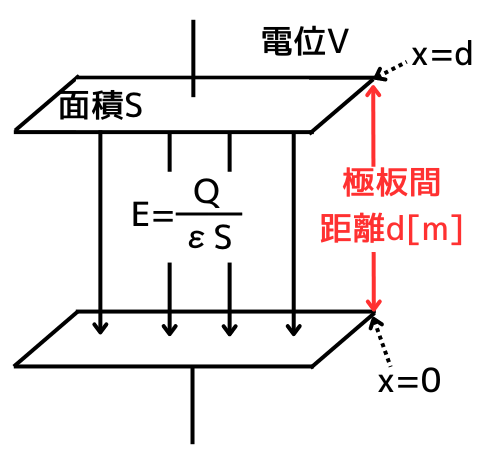
\(Q[C]\)の電荷が出す電気力線の本数は\(\displaystyle N=\frac{Q}{ε}[本]\)です。
電界の強さ\(E[V/m]\)は、電気力線の本数の密度と等しいので、
\(\displaystyle E=\frac{N}{S}=\frac{Q}{εS}\)
の式で表されます。
誘電率\(ε[F/m]\)、比誘電率\(ε_r\)、真空の誘電率\(ε_0[F/m]\)の関係は、
\(ε=ε_rε_0\)
なので、
\(\displaystyle E=\frac{Q}{ε_rε_0S}\)
となります。
\(S[m^2]\)は、極板の面積なので、定数として扱えます。
平行平板コンデンサの電界E[V/m]と電位V[V]
平行平板コンデンサの電界\(E[V/m]\)と電位\(V[V]\)の関係を示す式
\(V=Ed\) ⇔ \(\displaystyle E=\frac{V}{d}\)
極板間距離\(d[m]\)は定数。

\(V=Ed\)を導出します。
電位\(V[V]\)は、1Cの電荷を基点から対象点へ動かすときの仕事です。
基点はコンデンサの上端で\(d[m]\)
対象点はコンデンサの下端で\(0[m]\)
としたとき、電界の強さ\(E\)と電位\(V\)の関係は次のように表されます。
\(\displaystyle \begin{eqnarray}
V&=&-\int_d^0E・dr=-\int_d^0\frac{Q}{εS}dr\\
&=&-\frac{Q}{εS}[r]_d^0=\frac{Q}{εS}d=Ed
\end{eqnarray}\)
以上より、\(V=Ed\)が導出できました。
平行平板コンデンサの等電位面
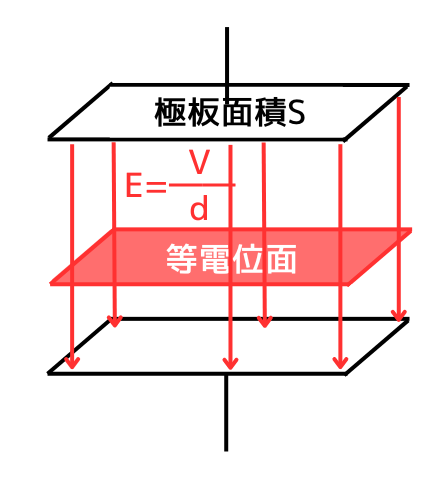
平行平板コンデンサの電界\(E[V/m]\)の項目に示した通り、極板間の電界の強さ\(E\)は、どこでも同じ強度です。
そのため、
\(V=Ed\)で示される電位は、極板の形と同じ形となります。
つまり、電極板と誘電体の境界面に対して平行といえます。
電荷Qと電束密度D
電荷\(Q[C]\)と、電束密度\(D[C/m^2]\)の関係式
\(\displaystyle D=\frac{Q}{S}\)
式中の\(S\)は、閉曲面面積\(S[m^2]\)
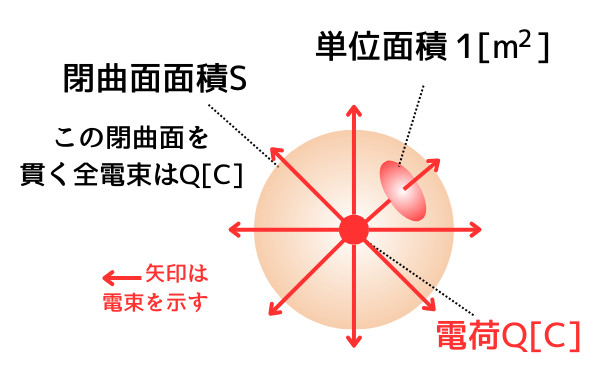
ガウスの法則
閉曲面を通って外へ出る電束の総数はその曲面内に含まれる全電気量に等しいという法則です。
式で示すと、
\(Q=\int_S \boldsymbol{D}・\boldsymbol{n}dS\)
ガウスの法則から、電荷\(Q[C]\)を囲む閉曲面を貫く全電束数は\(Q[C]\)です。
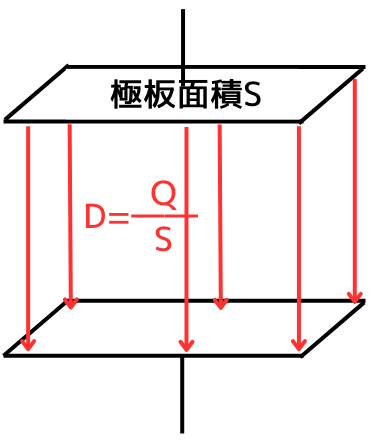
電束密度\(D[C/m^2]\)は、全電束数の密度です。
ここでいう密度とは、閉曲面の単位面積当たりの電束数を表すので、電束密度\(D[C/m^2]\)と電荷\(Q[C]\)の関係式は、極板面積\(S[m^2]\)を使って、
\(\displaystyle D=\frac{Q}{S}\)
と表されます。
コンデンサの電荷Q・静電容量C・電位Vの関係式
電荷\(Q[C]\)・静電容量\(C[F]\)・電位\(V[V]\)の関係式は、
\(Q=CV\)
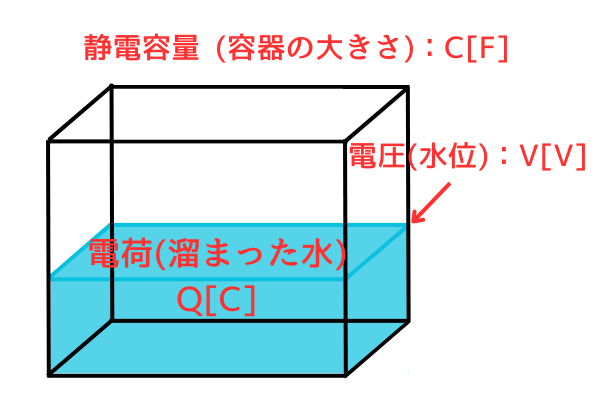
・電荷Q = 水槽に溜まった水量
・静電容量C = 水槽の大きさ
・電圧V = 水槽の水位
と考えると、容器が大きければ水量が増えても水位は増えずらく、容器が小さければわずかな水量でも水位はあがります。コンデンサでも、同様に考えられます。
平行平板コンデンサの誘電率ε・電荷量Q・静電容量C
平行平板コンデンサの静電容量\(C[F]\)の式は
\(\displaystyle C=ε\frac{S}{d}\)
平行平板コンデンサの静電容量\(C[F]\)の式を証明します。
平行平板コンデンサの電界E[V/m]と電位V[V]の要点整理から、
\(V=Ed\) ………①
平行平板コンデンサの電界E[V/m]の要点整理から、
\(\displaystyle E=\frac{Q}{εS}\) ………②
電荷Q・静電容量C・電位Vの関係式から、
\(Q=CV\)
⇔ \(\displaystyle C=\frac{Q}{V}\) ………③
これらより、静電容量の式が求められます。
③式に①・②式を代入していくと、次のように展開できます。
\(\displaystyle C=\frac{Q}{V}=\frac{Q}{Ed}=\frac{Q}{\frac{Q}{εS}d}=ε\frac{S}{d}\)
以上より、\(\displaystyle C=ε\frac{S}{d}\)が求められました。
静電エネルギーU[J]
静電エネルギーの式
\(\displaystyle U=\frac{1}{2}CV^2\)
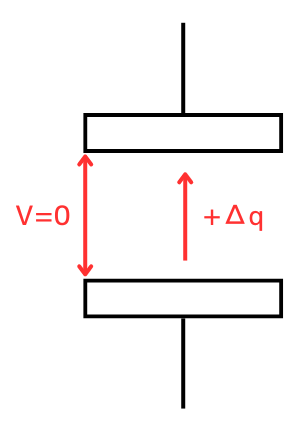
電位が\(V\)だけ大きいところに微小電荷\(Δq\)を動かすには、\(Δq・V\)の仕事が必要になります。
コンデンサ内に電荷が無い時、\(Δq\)を移動させるエネルギーは、\(V=0[V]\)なので、必要な仕事量\(ΔW_0=0[J]\)です。
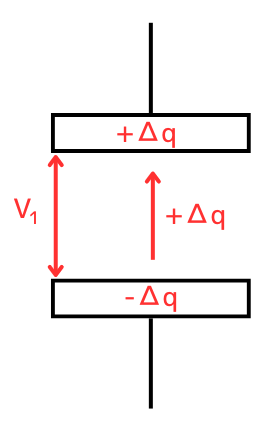
しかし、電荷を移動させていくと、\(\displaystyle V=\frac{q}{C}\)の関係から、電位差も大きくなっていきますので、必要な仕事量が増加していきます。
\(Δq\)が移動し、コンデンサの電位が\(V_1[V]\)になった時、次に\(Δq\)を移動させるエネルギーは、\(ΔW_1=ΔqV_1\)です。
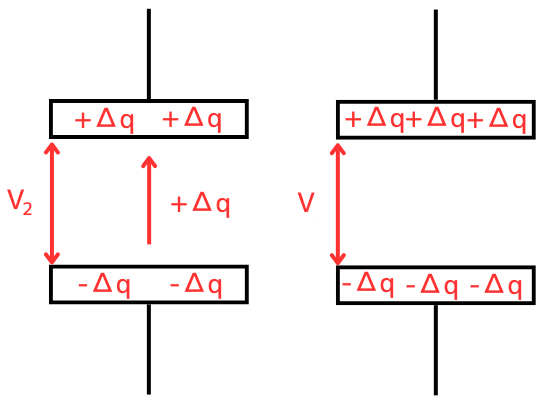
\(Δq\)が移動し、コンデンサの電位が\(V_2[V]\)になった時、
次に\(Δq\)を移動させるエネルギーは、\(ΔW_2=ΔqV_2\)と大きくなっていきます。
最終的に、電位\(V[V]\)になったとき、
電荷の移動がなくなったとします。
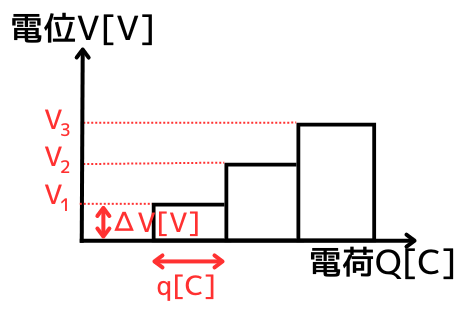
今までの微小電荷\(q[C]\)の溜まりと、コンデンサの電位\(V[V]\)の変化をグラフにすると、左図のようになります。
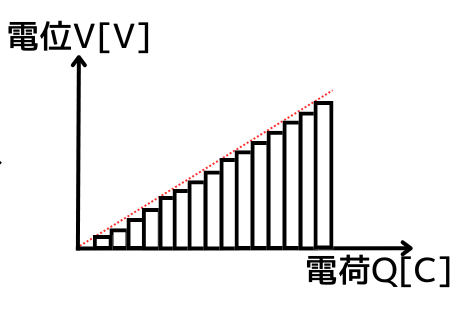
横軸をもっと細かくしていくと、直線グラフを描くことができます。
コンデンサは、\(q=0\)から、\(q=Q\)まで電荷を蓄えるので、
微小電荷が移動するエネルギー
\(ΔW=ΔqV\)
の式を、コンデンサに蓄えられた電荷が\(Q=0[C]\)から、\(Q=Q[C]\)になるまで積分すると、コンデンサに蓄えられる静電エネルギーが求められます。
実際に、積分をして静電エネルギーの式を求めます。
\(q=CV\)の式から、電位Vの式は、\(\displaystyle V=\frac{q}{C}\)です。
これを微小電荷\(Δq\)のエネルギー\(ΔW\)の式に代入すると、
\(\displaystyle ΔW=V・Δq=\frac{q}{C}Δq\)
静電エネルギー \(U[J]\)を求めるため、\(ΔW\)を積分すると、
\(\displaystyle U=\int_0^Q ΔW=\int_0^Q \frac{q}{C}dq=\left[ \frac{q^2}{2C} \right]_0^Q=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}CV^2 \)
以上より、
\(\displaystyle U=\frac{1}{2}CV^2\)
が求まりました。
回答解説
各選択肢について解説していきます。
(1) 誘電体内の等電位面は、電極板と誘電体の境界面に対して平行である。
平行平板コンデンサの等電位面の要点整理に記載したとおり、誘電体内の等電位面は、電極板と誘電体の境界面に対して平行です。
(2) コンデンサに蓄えられる電荷量は、誘電率が大きいほど大きくなる。
平行平板コンデンサの誘電率ε・電荷量Q・静電容量Cの要点整理から、
平行平板コンデンサの静電容量\(C[F]\)は\(\displaystyle C=ε\frac{S}{d}\)です。
電荷\(Q[C]\)は、\(Q=CV\)なので、
\(\displaystyle Q=CV=ε\frac{S}{d}V\)
となります。
したがって、コンデンサに蓄えられる電荷量は、誘電率\(ε[F/m]\)が大きい程大きくなります。
(3) 誘電体内の電界の大きさは、誘電率が大きいほど小さくなる。
この選択肢が間違っており、答えですが、よく考えないと引っかかってしまう可能性があります。
平行平板コンデンサの電界E[V/m]の要点整理に記載した、
\(\displaystyle E=\frac{Q}{εS}\)から、正しいとすると間違えです。
この式の電荷\(Q\)は、\(\displaystyle Q=CV=ε\frac{S}{d}V\)です。
この電荷\(Q\)の式を展開すると、
\(\displaystyle E=\frac{Q}{εS}=ε\frac{S}{d}V・\frac{1}{εS}=\frac{V}{d}\)
となります。
したがって、誘電体内の電界の大きさは、誘電率に影響を受けないが正しいです。
平行平板コンデンサの電界E[V/m]と電位V[V]の関係式から、
\(\displaystyle E=\frac{V}{d}\)の関係を使って回答すると早いです。
(4) 誘電体内の電束密度の大きさは、電極板の単位面積当たりの電荷量の大きさに等しい。
電荷\(Q[C]\)と、電束密度\(D[C/m^2]\)の関係式は、閉曲面面積\(S[m^2]\)を使って
\(\displaystyle D=\frac{Q}{S}\)です。
したがって、誘電体内の電束密度の大きさは、電極板の単位面積当たりの電荷量の大きさに等しいです。
(5) 静電エネルギーは誘電体内に蓄えられ、電極板の面積を大きくすると静電エネルギーは増大する。
静電エネルギーの式は、\(\displaystyle U=\frac{1}{2}CV^2[J]\)です。
コンデンサの静電容量\(C\)の式は、\(\displaystyle C=ε\frac{S}{d}\)なので、
静電エネルギーの式を書き直すと、\(\displaystyle U=\frac{1}{2}CV^2=\frac{1}{2}ε\frac{S}{d}V^2[J]\)
したがって、電極板の面積\(S[m^2]\)を大きくすると、静電エネルギー\(U[J]\)は増大します。
以上より、(3)が答えです。
出典元
一般財団法人 電気技術者試験センター
令和4年度第三種電気主任技術者試験 理論科目A問題上期問1
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント