難易度
直線状導体に電流が流れたときに生じる電磁力の計算問題です。
3本の直線状導体に流れた時の電磁力を計算する問題であるため、発生した電磁力をベクトル合成する必要がありますので少々応用が必要です。
問題
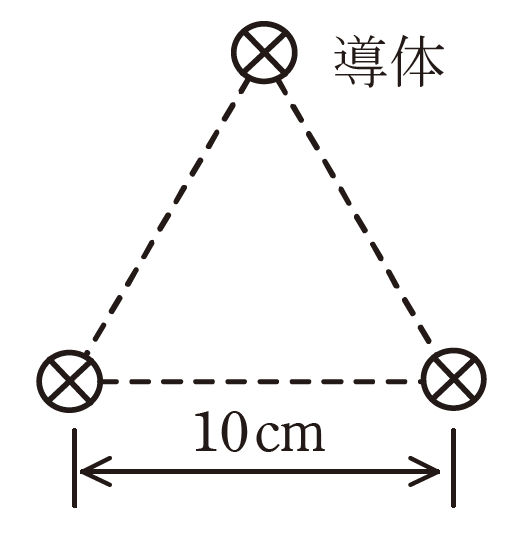
図のように、無限に長い3本の直線状導体が真空中に 10cm の間隔で正三角形の頂点の位置に置かれている。
3 本の導体にそれぞれ 7A の直流電流を同一方向に流したとき、各導体 1m 当たりに働く力の大きさ\(F_0[N/m]\)の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、無限に長い2本の直線状導体を\(r[m]\)離して平行に置き、2本の導体にそれぞれ\(I[A]\)の直流電流を同一方向に流した場合、各導体 1m 当たりに働く力の大きさ\(F\)の値[N/m]は,次式で与えられるものとする。
\(\displaystyle F=\frac{2I^2}{r}×10^{-7}\)
(1)\(0\)
(2)\(9.80×10^{-5}\)
(3)\(1.70×10^{-4}\)
(4)\(1.96×10^{-4}\)
(5)\(2.94×10^{-4}\)
答え
(3)
要点整理
電流と磁界の向き
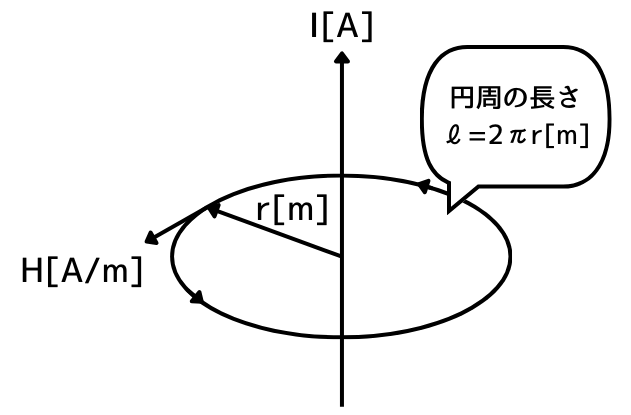
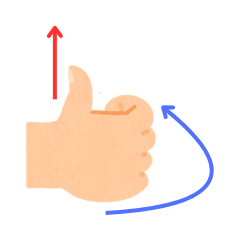
直線状導体に電流を流すと、電流を中心に同心円状の磁界が発生します。その向きは、右手で親指を立てたとき、
・電流:親指の向き
・磁界:他の指の向き
となります。
これを右ねじの法則と呼びます。
方位磁石のN極は、磁界の向きを指します。
アンペールの法則
電流が流れている直線状導体とアンペールの法則で覚える式は次の式です。
\(\displaystyle H=\frac{I}{2\pi r}[A/m]\)

解説
電流が作る磁界中で、磁界の強さが等しい所をたどって1周したときの磁路の長さ\(l=2\pi r[m]\)と、磁界の強さ\(H[A/m]\)の積が、電流\(I[A]\)に等しいという法則です。
式に示すと、
\( \displaystyle I=\oint_C Hdl\) \(=Hl=H\times 2\pi r \)
となります。変形すると、
\(\displaystyle H=\frac{I}{2\pi r}[A/m]\)
となります。
磁界と磁束密度について
磁界の強さ\(H[A/m]\)と、磁束密度\(B[T]\)の間には、
透磁率を\(μ\)、比透磁率を\(μ_r\)、真空の透磁率を\(μ_0\)としたとき、
\(B=μH=μ_rμ_0H\)
の関係があります。
電磁力について
電磁力は、電流と磁界の相互作用によって発生した力です。電磁力の式を端的に示すと下式となります。
\(F=IBlsinθ\)
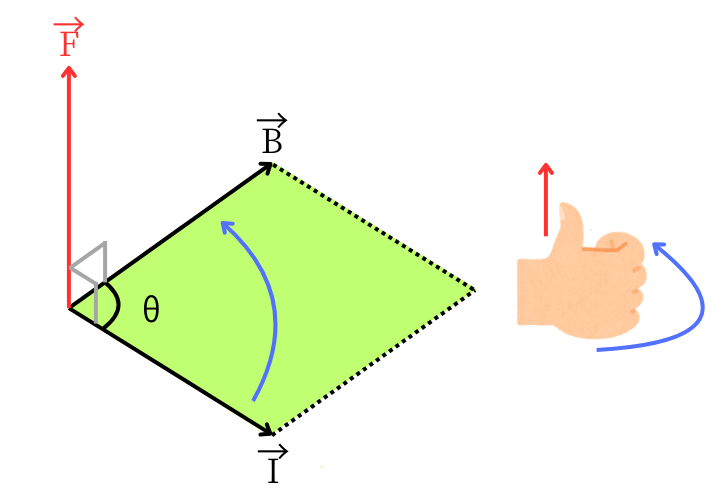
電磁力の式について解説します。
電磁力\(\vec{F}[N]\)は、電流\(\vec{I}[A]\)と、磁束密度\(\vec{B}[T]\)の外積で表されます。これを式で表すと、
\(\vec{F}=\vec{I}\times\vec{B}\)
となります。ベクトルの式に出てくる \(×\) の記号は、外積を表します。
電磁力の向きは、電流の向きから磁界の向きに右ねじの法則で回したときに、親指が向く向きです。
\(\vec{F}\)の大きさは、\(\vec{I}\)と\(\vec{B}\)の作る平行四辺形の面積と同じです。つまり、
\(|F|=|I| |B| sinθ\)
です。導体の長さを\(l[m]\)とすると
\(F=IBlsinθ\)
と求まります。
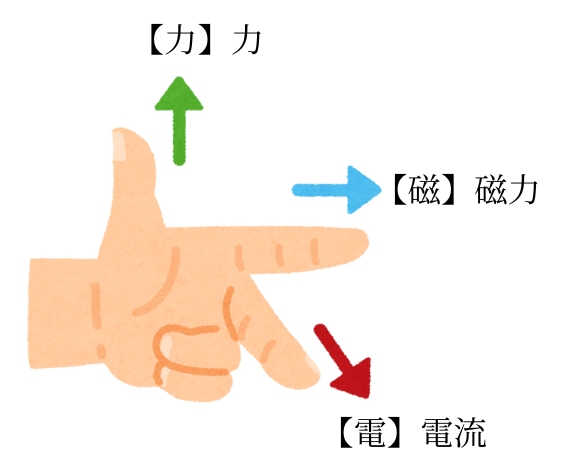
上記で示した電流・磁界・力の向きを簡単に表現すると、フレミング左手の法則で示されます。
回答解説

問題図中の各導体を、便宜的に上の導体を導体A、左下の導体を導体B、右下の導体を導体Cとします。
この時、導体Cに働く力の大きさ\(F[N/m]\)を求めます。
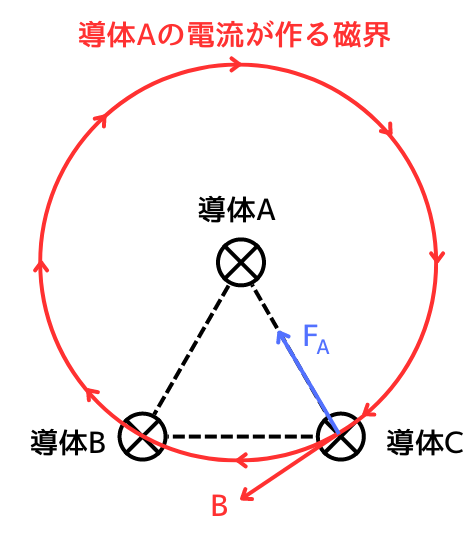
まず初めに、導体Aが作る磁界から、導体Cに発生する電磁力\(F_A[N/m]\)を求めます。
導体Aに流れる電流は、画面手前から奥に向かって行く方向の電流なので、右ねじの法則から時計回りの磁界が発生します。
導体Cも、画面手前から奥に向かって行く方向の電流が流れているので、フレミング左手の法則を使って、引っ張る方向に\(F_A\)が働きます。
問題文中に\(\displaystyle F=\frac{2I^2}{r}\)を示されていますが、本回答ではそれも導出します。
導体Aに流れる電流\(I[A]\)が作る磁界の強さ\(H[A/m]\)は、
\(\displaystyle H_A=\frac{I}{2πr}\)
磁束密度\(B\)と磁界の強さ\(H\)の関係から
\(\displaystyle B=μH=μ_0H=\frac{μ_0I}{2πr}\)
導体Cに働く電磁力は、
\(\displaystyle F_A=IBlsinθ=\frac{μ_0I^2}{2πr}\)
ここで、単位長さ当たりの電磁力を求めるので\(l=1[m]\)としました。
電流と磁界の向きは直角\((θ=90°)\)なので、\(sinθ=1\)としました。
真空の透磁率\(μ_0\)は、
\(μ_0=4π×10^{-7}[N/A^2]\)
\(μ_0\)を電磁力の式に代入すると、
\(\displaystyle F_A=\frac{μ_0I^2}{2πr}=\frac{2I^2}{r}×10^{-7}[N]\)
となり、問題文中の式が導出されました。
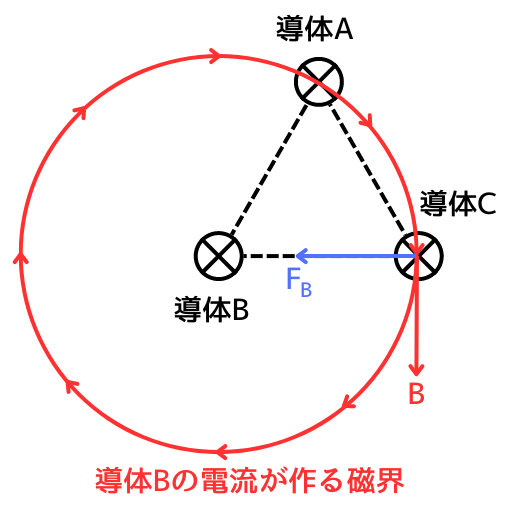
導体Bに流れる電流が導体Cに与える電磁力\(F_B\)も同様に求まります。
\(\displaystyle F_B=\frac{2I^2}{r}×10^{-7}[N]\)
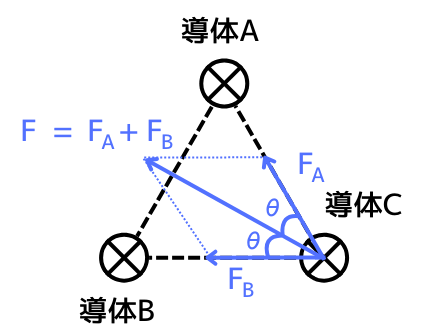
導体Cに働く力\(F\)は、\(F_A\)と、\(F_B\)のベクトル合成で得られます。
\(F\)と、\(F_A\)の間の角度θは、正三角形の角度の半分なので30°です。\(F\)と、\(F_B\)の間の角度θも同じです。
したがって、
\(\displaystyle \begin{eqnarray}
F&=&F_Acos30°+F_Bcos30°\\
&=&\frac{\sqrt{3}}{2}\frac{2I^2}{r}×10^{-7}+\frac{\sqrt{3}}{2}\frac{2I^2}{r}×10^{-7}\\
&=&\sqrt{3}・\frac{2I^2}{r}×10^{-7}\\
&=&\sqrt{3}・\frac{2・7^2}{0.1}×10^{-7}=1.70×10^{-4}[N/m]
\end{eqnarray}\)
以上より、(3)が答えです。
出典元
一般財団法人 電気技術者試験センター
令和4年度第三種電気主任技術者試験 理論科目A問題下期問4
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント