概要
電流帰還バイアス回路の計算問題です。
難しい問題です。トランジスタ回路に関する知識が深くないと解けない問題なので、この問題を選択した人はほとんど居ないのではないかと思われます。
キーワード
電流帰還バイアス回路
問題
図1の回路は、電流帰還バイアス回路に結合容量を介して、微小な振幅の交流電圧を加えている。
この入力電圧の振幅が \(A_i=100 mV\)、角周波数が\(ω=10 000 rad/s\)で、時刻 \(t[s]\)に対して \(v_i(t)[mV]\)が \(v_i(t)=A_isinωt\) と表されるとき、次の(a)及び(b)の問に答えよ。
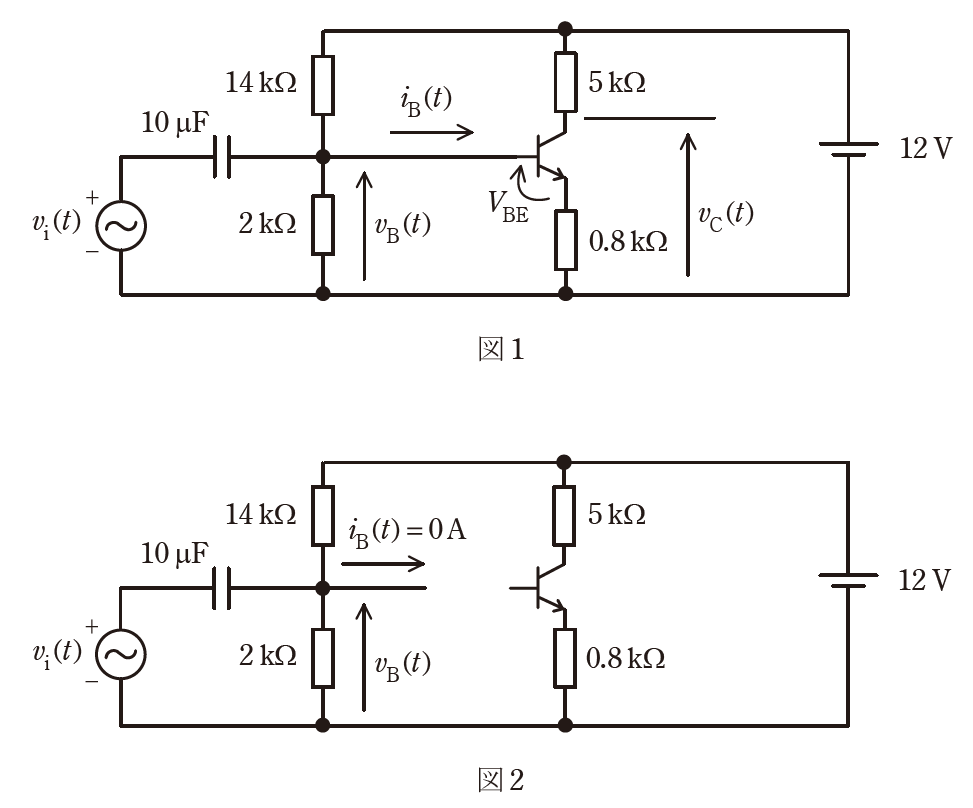
(a) 次の文章は、電圧\(v_B(t)\)に関する記述である。
トランジスタのベース端子に流れ込む電流\(i_B(t)\)が十分に小さいとき、ベース端子を切り離しても\(2 kΩ\) の抵抗の電圧は変化しない。
そこで、図2の回路で考え、さらに重ね合わせの理を用いることで、電圧\(v_B(t)\)を求める。
まず、\(v_i(t)=0 V\)とすることで、直流電圧\(V_B=\fbox{ (ア) } V\) が求められる。
次に、直流電圧源の値を\(0 V\) とし、コンデンサのインピーダンスが\(2 kΩ\)より十分に小さいと考えると、交流電圧\(v_B (t)\)の振幅 \(A_B=\fbox{ (イ) }mV\) と初期位相\(θ_B=\fbox{ (ウ) }rad\) が求められる。以上より、\(v_B(t)=V_B+A_Bsin(ωt+θ_B)\)と表すことができる。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
|---|---|---|---|
| (1) | 0.8 | 71 | 0 |
| (2) | 0.8 | 100 | \(\frac{π}{4}\) |
| (3) | 1.5 | 71 | \(\frac{π}{4}\) |
| (4) | 1.5 | 100 | 0 |
| (5) | 1.5 | 71 | 0 |
(b) 図1の回路の電圧\(v_C(t)\)を求め、適当な定数 \(V_C\)、\(A_C\)、\(θ_C\)を用いて
\(v_C(t)=V_C+A_Csin(ωt+θ_C)\)と表す。 \(V_C\)、\(A_C\)、\(θ_C\)に最も近い値の組合せを次の(1)~(5)のうちから一つ選べ。
ただし、ベース・エミッタ間電圧は常に0.7 V であると近似して考えてよい。
| \(V_C[V]\) | \(A_C[V]\) | \(θ_C[rad]\) | |
|---|---|---|---|
| (1) | 5 | 0.6 | 0 |
| (2) | 5 | 6 | 0 |
| (3) | 5 | 6 | \(π\) |
| (4) | 7 | 0.6 | \(π\) |
| (5) | 7 | 6 | \(π\) |
答え
(a)(4)
(b)(4)
解説テキスト リンク
回答解説
(a)の解答の流れ
①分圧の法則から\(V_B\)を求める
②コンデンサのインピーダンスが十分小さいことを使って\(A_B\)と\(θ_B\)を求める
①分圧の法則から\(V_B\)を求める
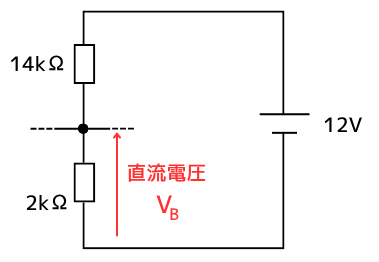
分圧の法則から
\(V_B=\frac{2×10^3}{2×10^3+14×10^3}・12=1.5V\)
したがって、\(V_B=\fbox{ (ア) } =1.5V\)です。
②コンデンサのインピーダンスが十分小さいことを使って\(A_B\)と\(θ_B\)を求める
問題文中の「コンデンサのインピーダンスが\(2kΩ\)より十分に小さいと考える」という条件から、\(10μF\)のカップリングコンデンサは無視しても問題ありません。
交流電圧に関して、問題文中の図2の回路図を更に簡素化して描きなおすと、下図のようになります。
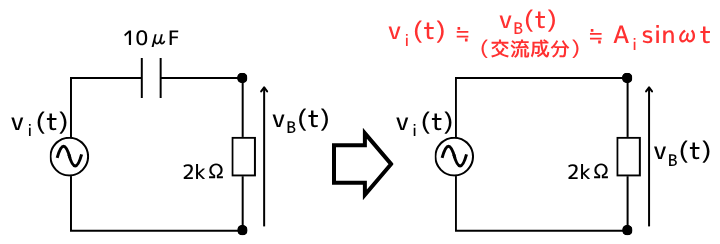
\(v_B(t)\)の交流成分は、\(v_B(t)=v_i(t)=A_isinωt\)となります。
したがって、
\(v_B(t)\)の交流成分の
・振幅\(A_B=\fbox{ (イ) }=A_i=100mV\)
・初期位相\(θ_B=\fbox{ (ウ) }rad=0rad\)
となります。
\(v_B(t)\)の直流成分と交流成分を合わせて記述すると、
\(v_B(t)=V_B+A_isinωt=1.5+0.1sinωt\)
となります。
以上より、(a)問題の答えは(4)です。
(b)の解答の流れ
①エミッタ電圧\(v_E(t)\)を求める
②エミッタ電流\(i_E(t)\)を求める
③コレクタ電流\(i_C(t)\)を求める
④コレクタ電圧\(v_C(t)\)を求める
①エミッタ電圧\(v_E(t)\)を求める
問題文中にベース・エミッタ間電圧\(V_{BE}\)は常に0.7 V であると近似して考えてよいとあるので、エミッタ電圧\(v_E\)は次のように計算できます。
\(v_E=v_B-V_E=1.5+0.1sinωt-0.7=0.8+0.1sinωt\)
整理すると、\(v_E=0.8+0.1sinωt\)と求まりました。
②エミッタ電流\(i_E(t)\)を求める
エミッタ電圧\(v_E\)、エミッタには\(R_E=0.8kΩ\)が接続されていることから、オームの法則を使って次のように計算できます。
\(\displaystyle \begin{eqnarray}
i_E&=&\frac{v_E(t)}{R_E}=\frac{0.8+0.1sinωt}{0.8×10^3}\\ \\
&=&(1.0+0.125sinωt)×10^{-3}[A]\\
&=&1.0+0.125sinωt [mA]
\end{eqnarray}\)
整理すると、\(i_E=1.0+0.125sinωt [mA]\)と求まりました。
③コレクタ電流\(i_C(t)\)を求める
ベース電流\(i_B(t)\)、コレクタ電流\(i_C(t)\)、エミッタ電流\(i_E(t)\)の関係は、
\(i_E(t)=i_C(t)+i_B(t)\)です。
\(i_C(t)\)に比べて、\(i_B(t)\)は非常に小さいので、
\(i_E(t)≒i_C(t)\) と近似できます。
したがって、\(i_C=1.0+0.125sinωt [mA]\) です。
④コレクタ電圧\(v_C(t)\)を求める
コレクタ電圧\(v_C(t)\)は、電源電圧\(12V\)から、\(5kΩ\)の抵抗の電圧降下した電圧なので、
\(\begin{eqnarray}
v_C(t)&=&12-5×10^3i_C(t)\\
&=&12-5×10^3・(1.0+0.125sinωt)×10^{-3}\\
&=&12-5.0-0.625sinωt\\
&=&7.0+0.625(sinωt+π)
\end{eqnarray}\)
問題文中の\(v_C(t)=V_C+A_Csin(ωt+θ_C)\)と比較すると、
・\(V_C=7.0V\)
・\(A_C=0.625≒0.6V\)
・\(θ_C=π\)
とわかりました。
以上より、(b)問題の答えは(4) です。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度上期 第三種電気主任技術者試験 理論科目B問題問18
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント