概要
静電気力の問題です。
(a)問題は基礎問題なので、確実に回答したい問題です。
(b)問題は基礎~普通レベルの問題です。導体球を接触させたときの電荷の移動をしっかりと計算できれば問題ないでしょう。
キーワード
静電気力、電荷の移動
問題
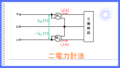
大きさが等しい二つの導体球A、B がある。
両導体球に電荷が蓄えられている場合、両導体球の間に働く力は。導体球に蓄えられている電荷の積に比例し、導体球間の距離の2 乗に反比例する。
次の(a)及び(b)の問に答えよ。
ただし、両導体球の大きさは\(0.3 m\) に比べて極めて小さいものとする。
(a) この場合の比例定数を求める目的で、導体球 A に\(+2×10^{-8}C\)、導体球 B に\(+3×10^{-8}C\)の電荷を与えて、導体球の中心間距離で \(0.3 m\) 隔てて両導体球を置いたところ、両導体球間に\(6×10^{-5} N\) の反発力が働いた。
この結果から求められる比例定数\([N・m^2/C^2]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、導体球A、B の初期電荷は零とする。
(1) \(3×10^9\) (2) \(6×10^9\) (3) \(8×10^9\) (4) \(9×10^9\) (5) \(15×10^9\)
(b) 小問(a)の導体球A、B を、電荷を保持したままで\(0.3 m\) の距離を隔てて固定した。
ここで、導体球A、B と大きさが等しく電荷を持たない導体球C を用意し、導体球C をまず導体球A に接触させ、次に導体球B に接触させた。
この導体球C を図のように導体球A と導体球B の間の直線上に置くとき、導体球Cが受ける力が釣り合う位置を導体球A との中心間距離\([m]\)で表したとき、その距離に最も近いものを次の(1)~(5)のうちから一つ選べ。
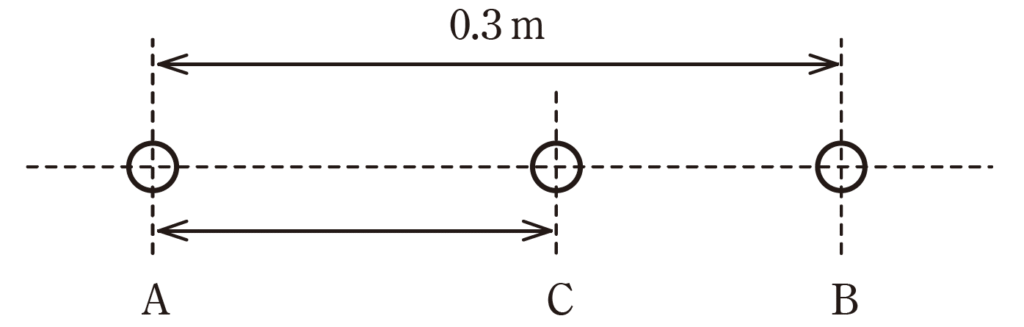
(1) 0.095 (2) 0.105 (3) 0.115 (4) 0.124 (5) 0.135
答え
(a)(4)
(b)(4)
解説テキスト リンク
回答解説
(a)の解答の流れ
①静電気力の式から比例定数を計算する
①静電気力の式から比例定数を計算する
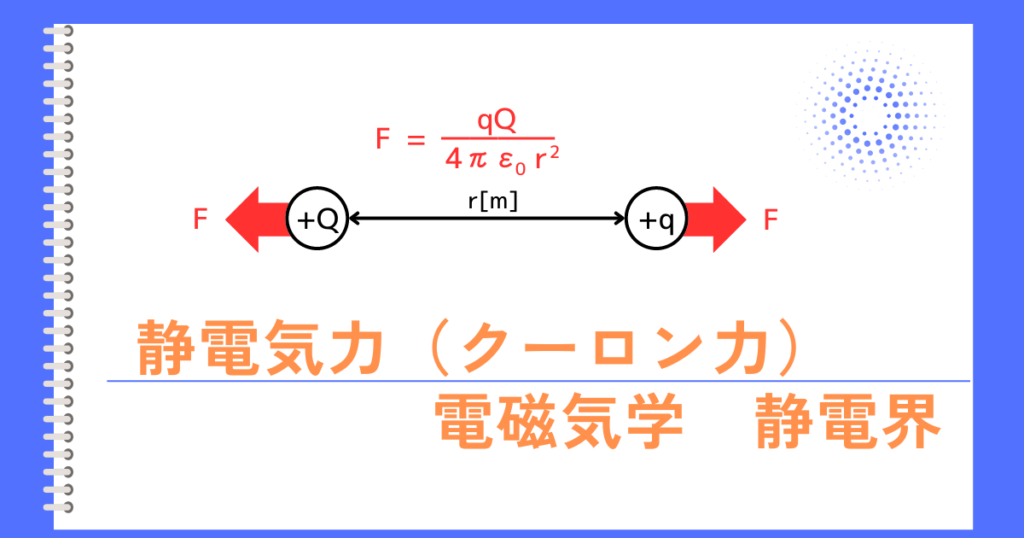
点電荷の静電気力の式は、
\(\displaystyle F=\frac{Q_1Q_2}{4πε_0r^2}=k\frac{Q_1Q_2}{r^2}\)
です。
・導体球Aの電荷\(Q_1=2×10^{-8}C\)
・導体球Bの電荷\(Q_2=3×10^{-8}C\)
・両導体球の距離\(r=0.3m\)
・静電気力\(F=6×10^{-5}N\)
を代入すると、比例定数kは次のように求まります。
\(\displaystyle k=\frac{6×10^{-5}・0.3^2}{2×10^{-8}・3×10^{-8}}=9×10^{-9}\)
以上より、(a)問題の答えは(4)\(9×10^{-9}\) が答えです。
(b)の解答の流れ
①導体球A・Cを接触させたときの電荷を求める
②導体球B・Cを接触させたときの電荷を求める
③静電気力がつり合う距離\(r\)を求める
①導体球A・Cを接触させたときの電荷を求める
導体球A・Cを接触させる前の電荷\(Q_A\)、\(Q_C\)
\(Q_A=2×10^{-8}\)、\(Q_C=0\)です。
導体球A・Cを接触させた後の電荷\(Q’_A\)、\(Q’_C\)は、
\(\displaystyle Q’_A=Q’_C=\frac{Q_A+Q_C}{2}=\frac{2×10^{-8}+0}{2}=1×10^{-8}\)です。
②導体球B・Cを接触させたときの電荷を求める
導体球B・Cを接触させる前の電荷\(Q_B\)、\(Q’_C\)
\(Q_B=3×10^{-8}\)、\(Q’_C=1×10^{-8}\)です。
導体球B・Cを接触させた後の電荷\(Q’_B\)、\(Q”_C\)は、
\(\displaystyle Q’_B=Q”_C=\frac{Q_B+Q’_C}{2}=\frac{3×10^{-8}+1×10^{-8}}{2}=2×10^{-8}\)です。
③静電気力がつり合う距離\(r\)を求める
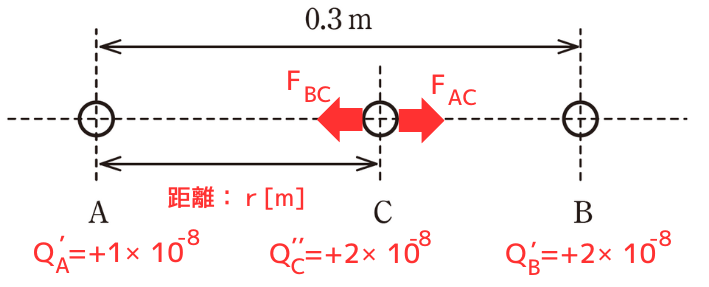
静電気力の式を立式します。
・導体球AC間の静電気力\(F_{AC}\)
\(\displaystyle F_{AC}=k・\frac{2×10^{-16}}{r^2}\)
・導体球BC間の静電気力\(F_{BC}\)
\(\displaystyle F_{BC}=k・\frac{4×10^{-16}}{(0.3-r)^2}\)
\(F_{AC}=F_{BC}\)なので、
\(\displaystyle k\frac{2×10^{-16}}{r^2}=k\frac{4×10^{-16}}{(0.3-r)^2}\)
⇔\(\displaystyle (0.3-r)^2=2r^2\)
⇔\(\displaystyle r^2+0.6r-0.09=0\)
二次方程式の解の公式から、
\(\displaystyle r=\frac{-0.6±\sqrt{0.6^2-4・1・(-0.09)}}{2}=0.124\)
なお、もう一つの解である-0.724は不適切なので、\(r=0.124[m]\)と求まります。
以上より、(b)問題の答えは(4)0.124 です。
二次方程式の解の公式
\(ax^2+bx+c=0\)の二次方程式の解\(x\)は、解の公式から求められます。
\(\displaystyle x=\frac{-b±\sqrt{b^2-4ac}}{2a}\)
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度上期 第三種電気主任技術者試験 理論科目B問題問16
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント