概要
電磁誘導に関する基礎的な問題です。
電磁誘導によって、誘導起電力が発生するまでの流れを理解していれば簡単に回答できます。
キーワード
右ねじの法則、磁束鎖交数、誘導起電力、ファラデーの電磁誘導の法則
問題
次の文章は、電磁誘導に関する記述である。
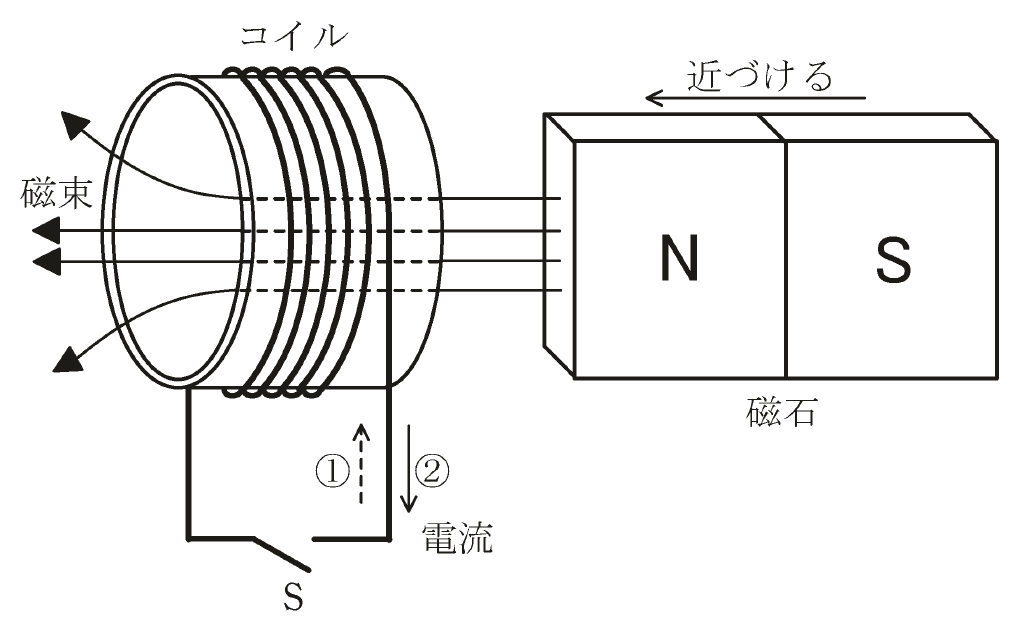
図のように、コイルと磁石を配置し、磁石の磁束がコイルを貫いている。
- スイッチSを閉じた状態で磁石をコイルに近づけると、コイルには ア の向きに電流が流れる。
- コイルの巻数が\(200\)であるとする。
スイッチSを開いた状態でコイルの断面を貫く磁束を\(0.5s\)の間に\(10mWb\)だけ直線的に増加させると、磁束鎖交数は イ \(Wb\)だけ変化する。
また、この\(0.5s\)の間にコイルに発生する誘導起電力の大きさは ウ \(V\)となる。ただし、コイル断面の位置によらずコイルの磁束は一定とする。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、正しい物を次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
| (1) | ① | 2 | 2 |
| (2) | ① | 2 | 4 |
| (3) | ① | 0.01 | 2 |
| (4) | ② | 2 | 4 |
| (5) | ② | 0.01 | 2 |
答え
(4)
要点整理
磁束変化と電流を作る向き
コイル内を貫く磁束が変化した時、それを妨げる方向にコイルが磁束を作ります。
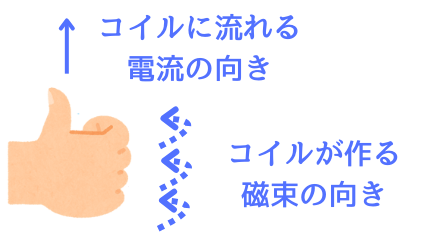
コイルの磁束変化時に、コイルに流れる電流の向きはは、右ねじの法則からわかります。
・親 指:コイルが作る磁束の向き
・他の指:電流の向き
磁石をコイルに近づけた時に、コイルに電流が流れるまでの流れは次の通りです。
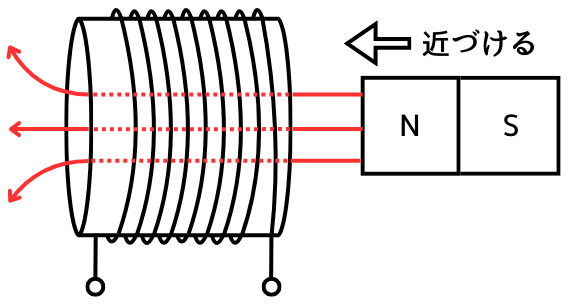
①磁石をコイルに近づけると、コイルを貫く磁束が増加します。
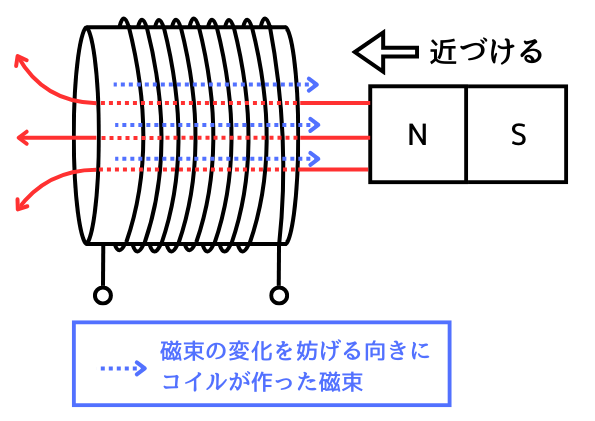
②妨げる方向にコイルが磁束を作ります。
つまり、磁石が近づいたことで増加した磁束を減らす方向に磁束を作ります。
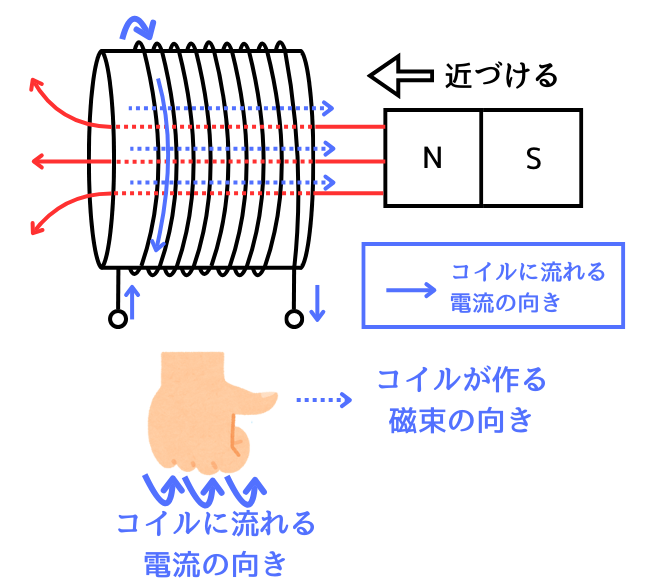
③右ねじの法則の向きに、コイルに電流が流れます。
右ねじの法則 補足

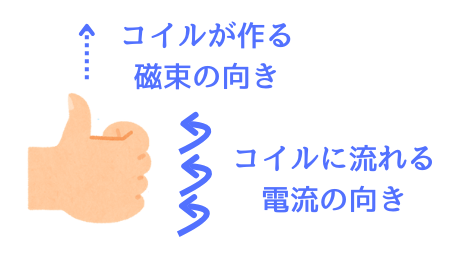
右ねじの法則は、「電流の向き」と「磁束の向き」を紐づける法則です。
右手でグッドサインを作ったときに、親指の向きと、他の丸めた指の向きが、それぞれ電流の向き・磁束の向きを示します。
この向きの紐づけは、上図の通り、親指を電流・磁束の向きのどちらにしても成り立ちます。
磁束鎖交数
磁束鎖交数\(\Phi[Wb]\)とは、コイル全体を貫く磁束のことです。
コイルの巻数が\(N\)[回]、磁束を\(\phi[Wb]\)とした時、
\(\phi[Wb]\)の磁束が、コイルの巻線を\(N\)回貫くことになるので、磁束鎖交数は次の式で表されます。
\(\Phi=N\phi [Wb]\)
磁束鎖交数\(\Phi\)は、コイルのインダクタンスを\(L[H]\)、コイルに流れる電流\(I[A]\)のとき、次の式で表されます。
\(\Phi=LI [Wb]\)
磁束鎖交数は\(\Phi\) (大文字のファイ)
磁束は\(\phi\) (小文字のファイ)
の記号で表しますので、大文字の\(\Phi\)と、小文字の\(\phi\)に注意。
磁束変化による逆起電力(ファラデーの電磁誘導の法則)
コイルを貫く磁束を変化させると、誘導起電力\(e[V]\)が発生します。
この現象を、ファラデーの電磁誘導の法則と呼びます。
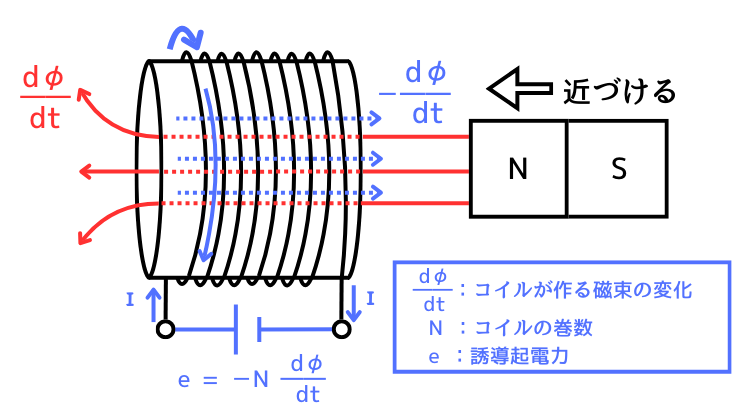
誘導起電力\(e[V]\)の大きさは、コイルの巻数\(N\)[回]、磁束の時間変化量\(\frac{d\phi}{dt}\)としたとき、次式で表されます。
\(\displaystyle e=-N\frac{d\phi}{dt}\)
回答解説
ア



要点整理の「磁束変化と電流を作る向き」の項目で記載した通り、N極の磁石を近づけた時の磁石が作る磁束の変化を妨げる向きに、コイルが磁束を発生させます。
そして、コイルが発生させた磁束の向きと右ねじの法則で合わせた向きに電流が流れます。
したがって、(ア)の答えは②です。
イ
磁束鎖交数の変化量\(Δ\Phi[Wb]\)は、\(Δ\Phi=-NΔ\phi\)です。
問題文から、次の事がわかります。
・コイルの巻数\(N=200\)[回]
・磁束の変化\(Δ\phi=10×10^{-3}[Wb]\)
磁束鎖交数の式に代入すると、
\(Δ\Phi=-NΔ\phi=-200×10×10^{-3}=-2[Wb]\)
したがって、(イ)は2です。
ウ
誘導起電力\(e[V]\)は、\(e=-N\frac{d\phi}{dt}\)です。
問題文から、次の事がわかります。
・コイルの巻数\(N=200\)[回]
・磁束の変化\(\frac{d\phi}{dt}=\frac{10×10^{-3}}{0.5}=2×10^{-2}\)
磁束鎖交数の式に代入すると、
\(e=-N\frac{d\phi}{dt}=-200×2×10^{-2}=-4[V]\)
したがって、(ウ)は4です。
以上より、答えは(4)です。
出典元
令和3年度第三種電気主任技術者試験 理論科目A問題問4
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント