概要
誘電率\(ε\)が変化したとき、2つの導体小球間に働くクーロン力がどのように変化するかを問う問題です。クーロン力の式を理解していれば、簡単に解ける問題です。
キーワード
誘電率、クーロン力\(F[N]\)
問題
二つの導体小球がそれぞれ電荷を帯びており、真空中で十分な距離を隔てて保持されている。
ここで、真空の空間を、比誘電率2の絶縁体の液体で満たしたとき、小球の間に作用する静電力に関する記述として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1)液体で満たすことで、静電力の向きも大きさも変わらない。
(2)液体で満たすことで静電力の向きは変わらず、大きさは2倍になる。
(3)液体で満たすことで静電力の向きは変わらず、大きさは\(\frac{1}{2}\)倍になる。
(4)液体で満たすことで静電力の向きは変わらず、大きさは\(\frac{1}{4}\)倍になる。
(5)液体で満たすことで静電力の向きは変わらず、大きさは変わらない。
答え
(3)
要点整理
点電荷が作る電界の強さE[V/m]
点電荷\(Q[C]\)が、誘電率\(ε\)の誘電体中に作る電界の強さ\(E[V/m]\)は、次式で示されます。
\(\displaystyle E=\frac{Q}{4πεr^2}\)
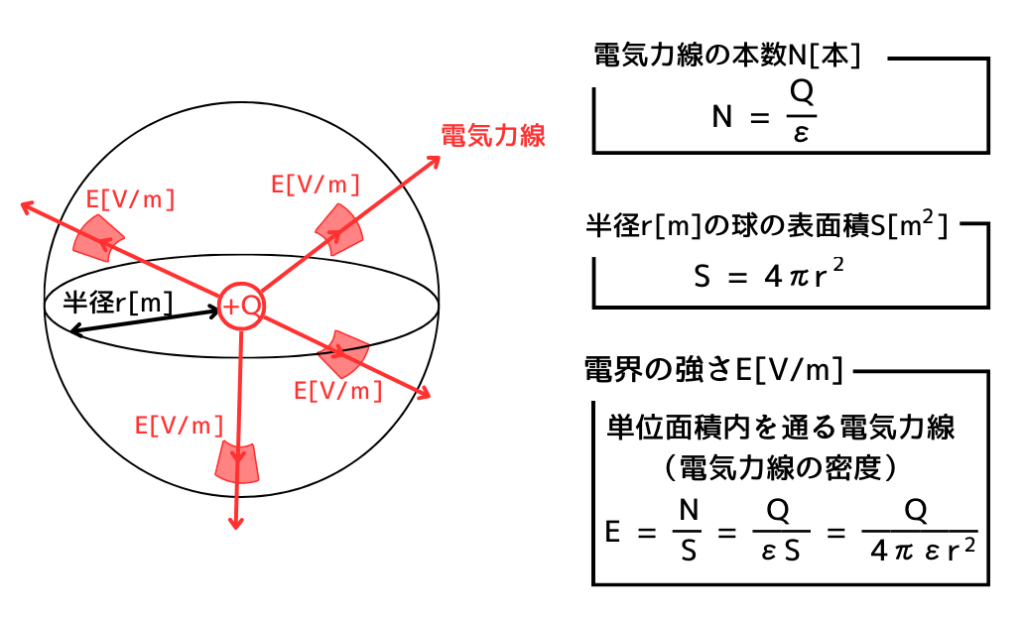
\(Q[C]\)の点電荷が出す電気力線の本数は、\(N=\frac{Q}{ε}[本]\)で、放射状に広がります。
半径\(r[m]\)の地点での閉曲面の面積は、電気力線が放射状に広がることから球の表面積となります。したがって、\(S=4πr^2[m^2]\)です。
そして、電界の強さ\(E[V/m]\)は、点電荷\(Q\)から半径\(r[m]\)の閉曲面を貫く電気力線の密度ですので、電界の強さ\(E[V/m]\)は、次式で表されます。
\(\displaystyle E=\frac{N}{S}=\frac{Q}{εS}=\frac{Q}{4πεr^2}\)
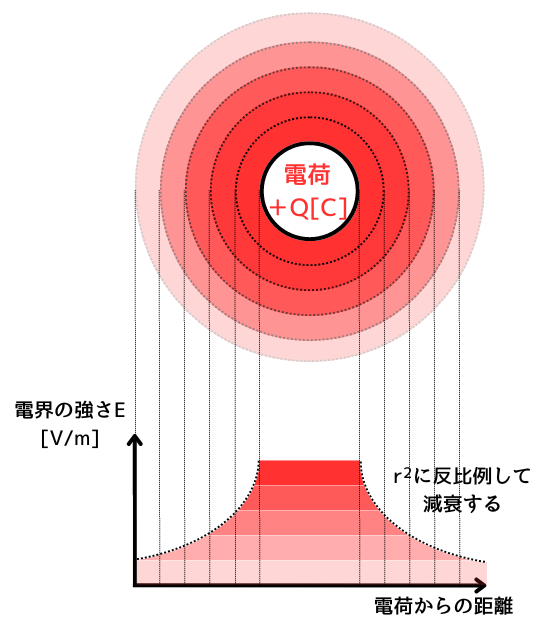
電荷\(+Q[C]\)から、\(r[m]\)離れた点の電界の強さ\(E[V/m]\)の減衰の様子を、図示すると、左図のようになります。
\(\displaystyle E=\frac{Q}{4πεr^2}\)の式から、電界の強さ\(E[V/m]\)について次のことがわかります。
・電荷\(Q[C]\)に比例する
・誘電率\(ε[F/m]\)に反比例する
・電荷からの距離\(r[m]\)の二乗に反比例する
2つの点電荷間に働くクーロン力F[N]
クーロン力の働く向き
・「正電荷-正電荷」「負電荷-負電荷」の符号が同じ時、電荷間に反発力が働く。
・「正電荷-負電荷」の符号が違う時、電荷間に引力が働く。
クーロン力の大きさ
二つの点電荷が\(Q[C]\)、\(q[C]\)としたとき、二つの点電荷には、次の式で示されるクーロン力が働きます。
\(\displaystyle F=\frac{Qq}{4πεr^2}\)
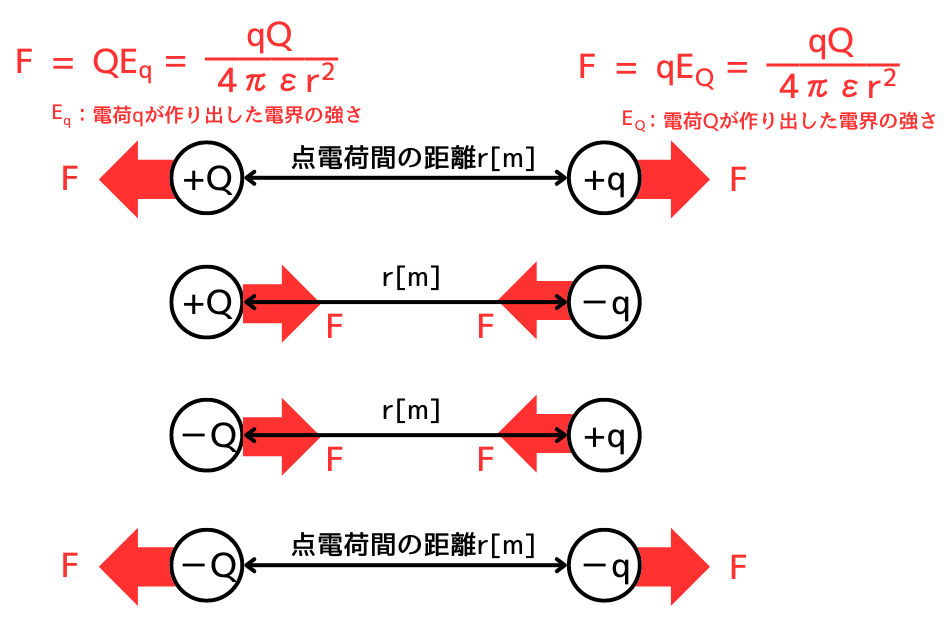
クーロン力の働く向きは、左図のとおり、電荷の符号で決まります。
電荷\(Q[C]\)が作り出した電界\(E_Q[V/m]\)内に存在する電荷\(q[C]\)に働くクーロン力\(F[N]\)は、次式となります。
\(\displaystyle F=qE_Q=q\frac{Q}{4πεr^2}=\frac{qQ}{4πεr^2}\)
電荷\(q[C]\)が作り出した電界\(E_q[V/m]\)内に存在する電荷\(Q[C]\)に働くクーロン力\(F[N]\)は、次式となります。
\(\displaystyle F=QE_q=Q\frac{q}{4πεr^2}=\frac{qQ}{4πεr^2}\)
以上のことから、どちらの電荷にも同じ大きさのクーロン力\(F[N]\)が働きます。
回答解説
静電力(クーロン力)の作用する向きと、大きさについて、それぞれ考えて行きます。
【静電力(クーロン力)の作用する向き】
静電力(クーロン力)の作用する向きは、
「正電荷-正電荷」「負電荷-負電荷」のように極性が同じ時は反発する方向に作用します。
「正電荷-負電荷」「負電荷-正電荷」のように極性が違う時は吸引する方向に作用します。
つまり、二つの導体小球が帯びている電荷の極性によって決まりますので、電荷の周囲を満たす物質の比誘電率によって静電力の向きは変わりません。
【静電力(クーロン力)の大きさ】
静電力(クーロン力)の式は、二つの導体小球が帯びている電荷をそれぞれ\(+Q[C]\)、\(+q[C]\)としたとき、次の①式で表されます。
\(\displaystyle F=\frac{qQ}{4πεr^2}\) ………①
\(ε\)は誘電率です。
真空の誘電率を\(ε_0\)、比誘電率を\(ε_r\)としたとき、
\(ε=ε_rε_0\) ………②
となります。
真空の空間で働く静電力\(F_0\)の大きさは、
\(\displaystyle F_0=\frac{qQ}{4πε_0r^2}\) ………③
比誘電率\(ε_r=2\)の絶縁体の液体で満たした時に働く静電力\(F_2\)の大きさは、
\(\displaystyle F_2=\frac{qQ}{4πε_rε_0r^2}=\frac{qQ}{8πε_0r^2}\) ………④
③・④式を比較すると、\(F_2=\frac{1}{2}F_0\)なので、
静電力の大きさは\(\frac{1}{2}\)倍になります。
以上より、(3)が答えとなります。
出典元
一般財団法人 電気技術者試験センター
令和3年度第三種電気主任技術者試験 理論科目A問題問2
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント