概要
静電界のクーロン力と、磁界のローレンツ力の問題です。
二つの力を合成して考える必要があります。
難しくない部類の問題ですが、静電界と磁界の両方について学んでいる必要があります。
キーワード
静電界、磁界、クーロン力、ローレンツ力、力の合成
問題
図のように、x方向の平等電界\(E[V/m]\)、y方向の平等磁界\(H[A/m]\)が存在する真空の空間において、電荷\(-e[C]\)、質量\(m[kg]\)をもつ電子がz方向の初速度\(v[m/s]\)で放出された。
この電子が等速直線運動をするとき、\(v\)を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、真空の誘電率を\(ε_0[F/m]\)、真空の透磁率を\(μ_0[H/m]\)とし、重力の影響を無視する。
また、電子の質量は変化しないものとする。
図中の ◉ は紙面に垂直かつ手前の向きを表す。
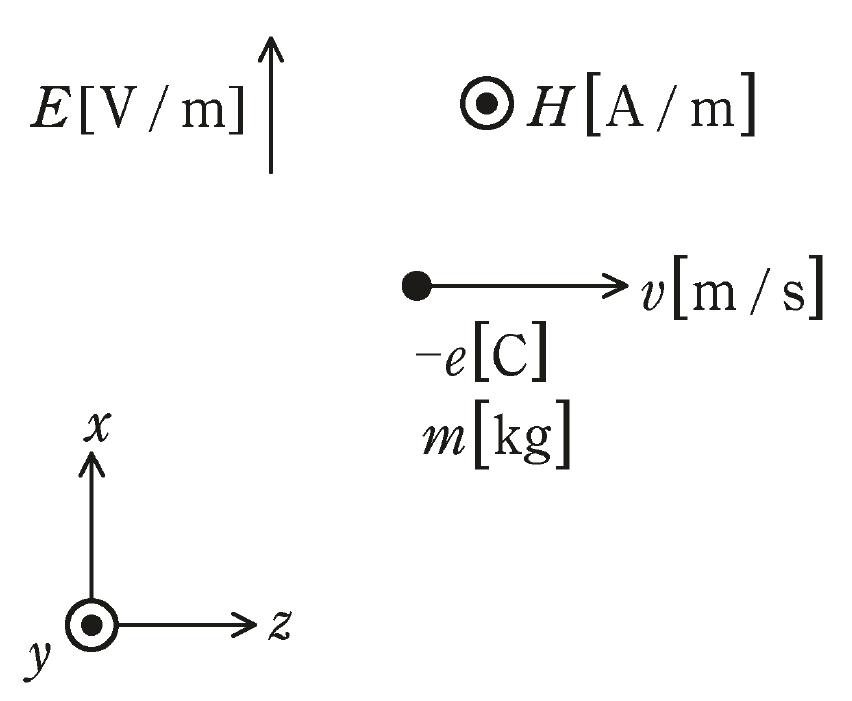
(1)\(\displaystyle \frac{ε_0E}{μ_0H}\) (2)\(\displaystyle \frac{E}{H}\) (3)\(\displaystyle \frac{E}{μ_0H}\)
(4)\(\displaystyle \frac{H}{ε_0E}\) (5)\(\displaystyle \frac{μ_0H}{E}\)
答え
(3)
解説テキスト リンク
回答解説
解答の流れ
①電界から受けるクーロン力\(F_E\)を考える
②磁界から受けるローレンツ力\(F_B\)を考える
③クーロン力とローレンツ力の釣り合いから電荷の速度\(v\)を求める
①電界から受けるクーロン力\(F_E\)を考える
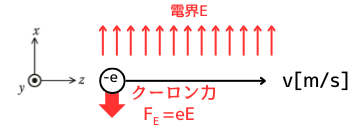
電界\(E\)が\(+x\)方向に向いているので、電界から受けるクーロン力\(F_E\)は、\(-x\)方向に向きます。
クーロン力\(F_E[N]\)の大きさは、
\(F_E=eE\)
②磁界から受けるローレンツ力\(F_H\)を考える
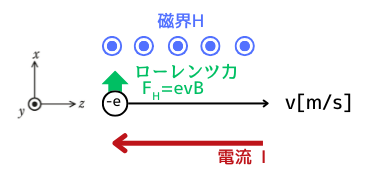
磁界\(H\)が\(+y\)方向(紙面に垂直かつ手前の向き)に向いています。
電子\(-e\)が\(+z\)方向に向かって移動しているため、電流\(I\)はその逆向きの\(-z\)方向に流れています。
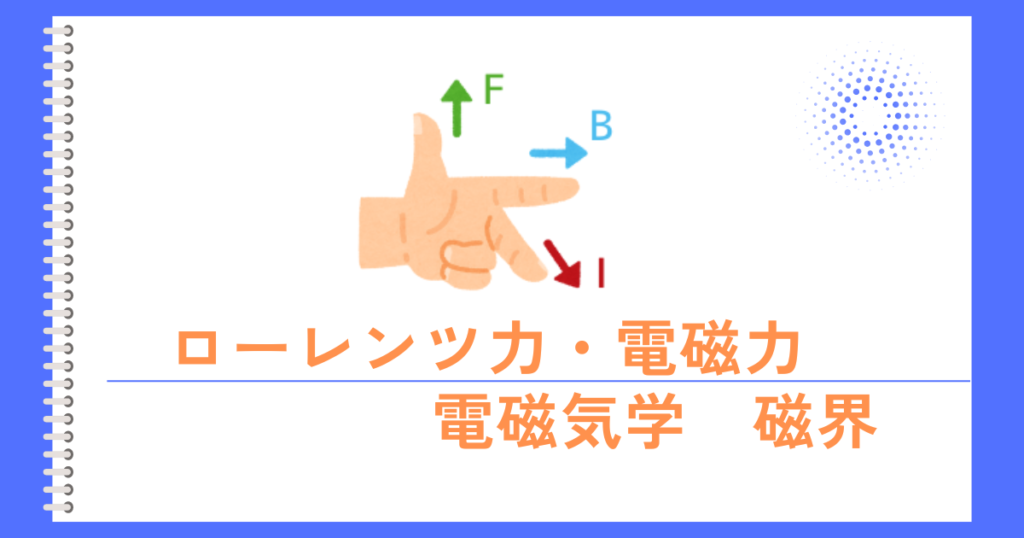
フレミング左手の法則
(親指)力の向き / (人差し指)磁界 / (中指)電流
から、磁界から受けるローレンツ力\(F_H\)は、\(+x\)方向に向きます。
磁束密度\(B[T]\)と、磁界強度\(H[A/m]\)の関係式は、真空の透磁率を\(μ_0[H/m]\)としたとき、
\(B=μ_0H\)
なので、ローレンツ力\(F_H[N]\)の大きさは、
\(F_H=evB=evμ_0H\)
③クーロン力\(F_E\)とローレンツ力\(F_H\)の釣り合いから電荷の速度\(v\)を求める
クーロン力\(F_E\)とローレンツ力\(F_H\)がつり合っていないと、電子が等速直線運動をすることはできないので、次式のように展開できます。
\(F_E=F_H\)
⇔\(eE=evμ_0H\)
⇔\(\displaystyle v=\frac{E}{μ_0H}\)
以上より、電子が等速直線運動をするときの電子の速度\(v\)は、(3)\(\displaystyle \frac{E}{μ_0H}\)となります。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和3年度 第三種電気主任技術者試験 理論科目A問題問12
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント