【電験三種：理論】令和３年度　問１０

概要

RL回路の過渡応答の問題です。
抵抗を変化させたさせたときの電流の大きさと、時定数の変化について問われている問題です。
過渡応答の中でも基礎問題です。

キーワード
RL回路、過渡応答、時定数

　

問題

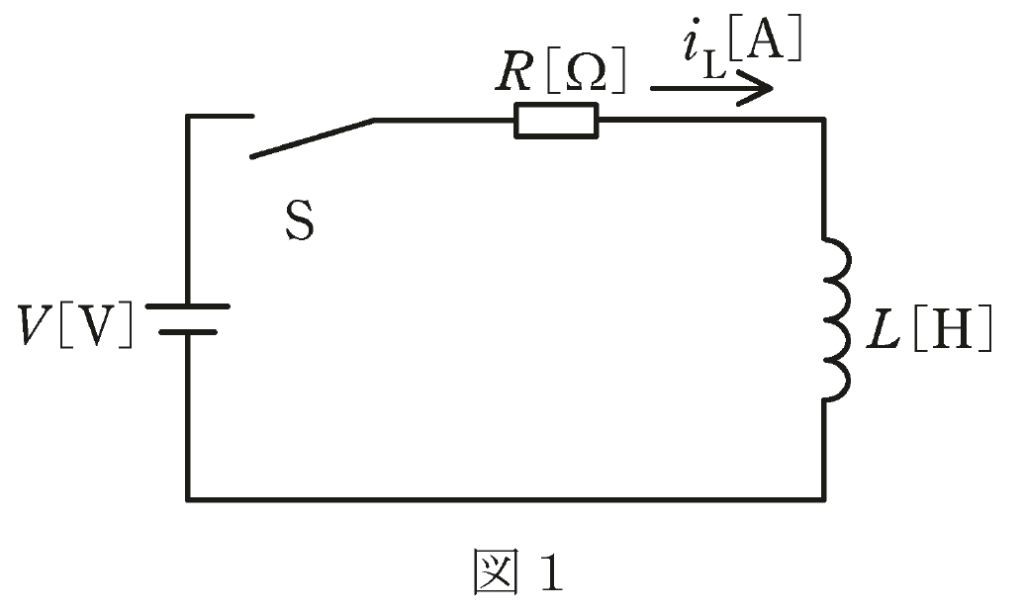
開放電圧が\(V[V]\)で出力抵抗が十分に低い直流電圧源と、インダクタンスが\(L[H]\)のコイルが与えられ、抵抗\(R[Ω]\)が図１のようにスイッチSを介して接続されている。

時刻\(t=0\)でスイッチSを閉じ、コイルの電流\(i_L[A]\)の時間に対する変化を計測して、波形として表す。

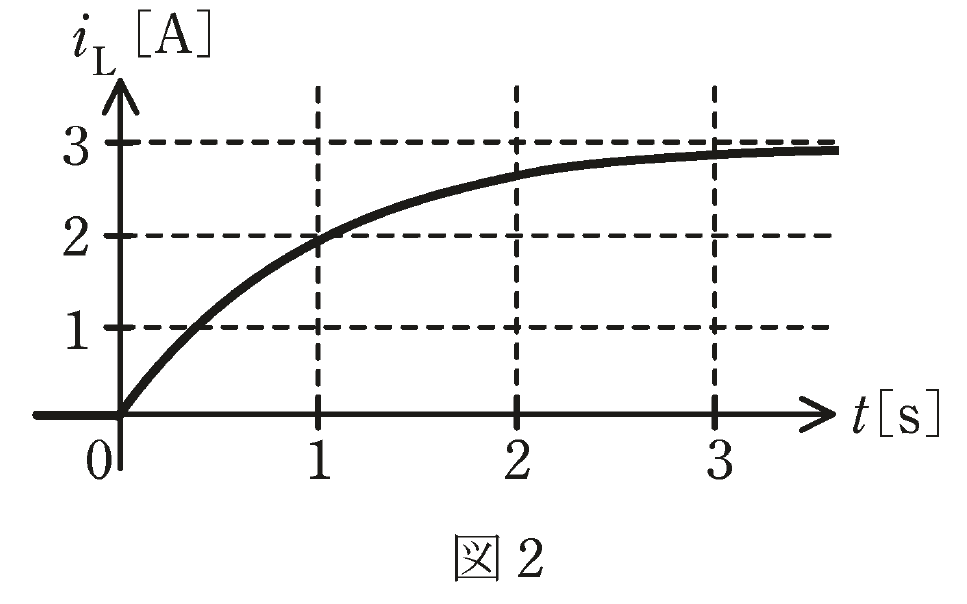
\(R=1Ω\)としたところ、波形が図２であったとする。
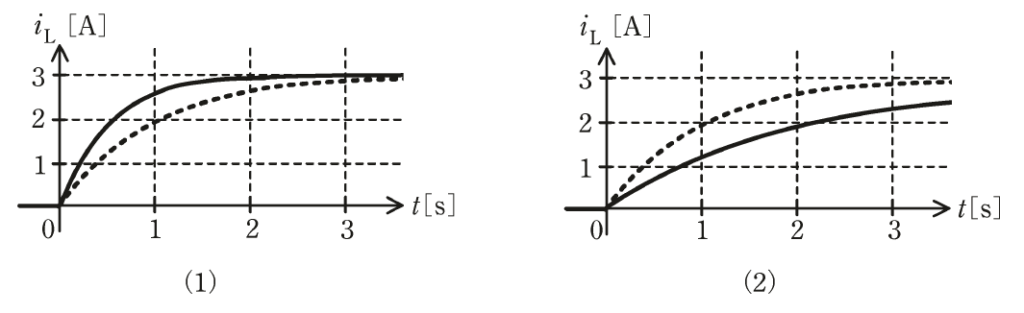
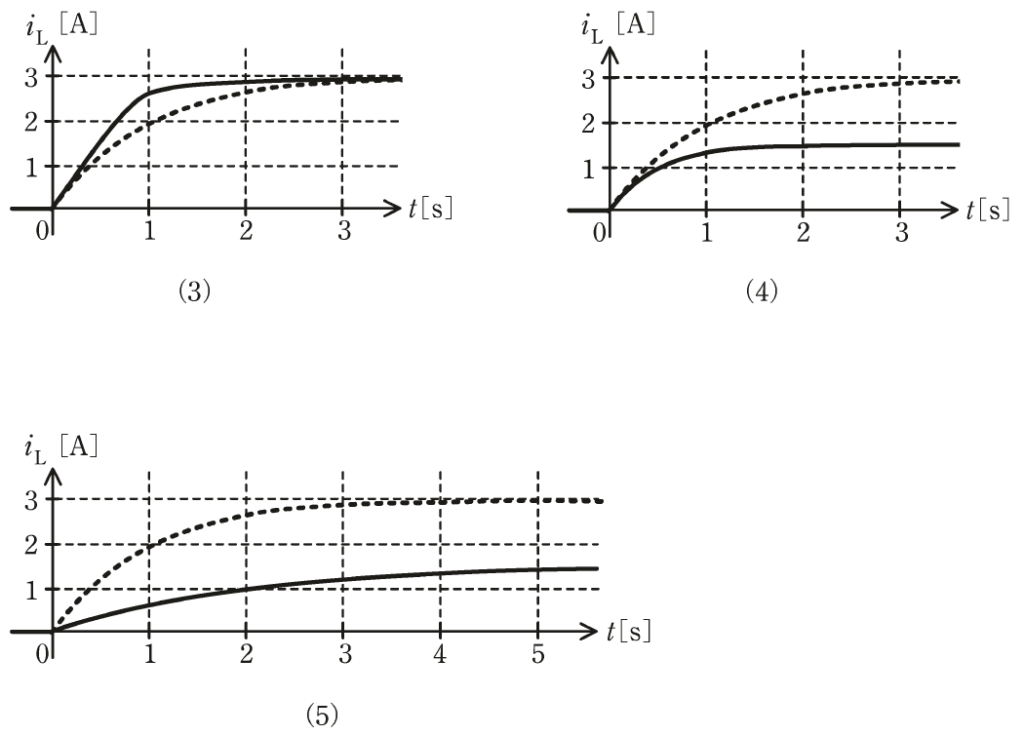
\(R=2Ω\)であればどのような波形となるか、波形の変化を最も適切に表すものを次の（１）～（５）のうちから一つ選べ。

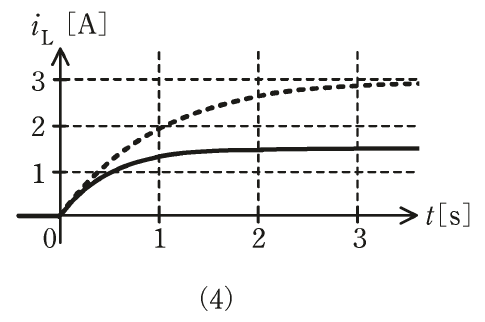
ただし、選択肢の図中の点線は図２と同じ波形を表し、実線は\(R=2Ω\)のときの波形を表している。

　

　

答え

(４)

解説テキスト　リンク

回答解説

　

回答の流れ
①RL回路の\(i_L\)について微分方程式を立てる
②過渡状態を解析する
③定常状態を解析する
④初期状態を解析する
⑤\(i_L\)の一般解を求める
⑥Rを変更前後の式を比較する

①RL回路の\(i_L\)について微分方程式を立てる
キルヒホッフの電圧則から、
\(V=v_R+v_L\)　…(1)

オームの法則から、
\(v_R=Ri_L\)　…(2)
\(v_L=L\frac{di_L}{dt}\)　…(3)

(1)式に(2)・(3)式を代入すると、
\(V=Ri_L+L\frac{di_L}{dt}\)

---

②過渡状態を解析する
過渡状態の電流を\(i_{Lt}\)とします。
\(i_{Lt}=ke^{-st}\)としたとき、
\(\frac{di_{Lt}}{dt}=-ske^{-st}\)

\(0=Ri_{Lt}+L\frac{di_{Lt}}{dt}=Rke^{-st}-Lske^{-st}=(R-Ls)ke^{-st}\)

⇔\(s=\frac{R}{L}\)　…(4)

---

③定常状態を解析する
定常状態の電流を\(i_{Ls}\)とします。
定常状態のとき、\(\frac{di_{Ls}}{dt}=0\)となります。
したがって、定常状態の回路の方程式は、
\(V=Ri_{Ls}\)　⇔　\(i_{Ls}=\frac{V}{R}\)

---

④初期状態を解析する
\(i_L\)は、過渡解\(i_{Lt}\)と定常解\(i_{Ls}\)を足し合わせた電流です。
\(i_L=i_{Lt}+i_{Ls}\)
スイッチSを閉じた直後である\(t=0s\)のとき、\(i_L\)の初期状態の電流を\(i_L(0)\)とします。
コイルは、状態変化をした直後は電流を完全に遮断するので、\(i_L(0)=0A\)です。
\(i_L(0)=i_{Lt}+i_{Ls}=ke^{-\frac{R}{L}0}+\frac{V}{R}=k+\frac{V}{R}=0\)
⇔\(k=-\frac{V}{R}\)

---

⑤\(i_L\)の一般解を求める
\(i_L\)は次のように求まります。
\(i_L=\frac{V}{R}\left( 1-e^{-\frac{R}{L}t}\right) \)

　

---

⑥Rを変更前後の式を比較する
問題のグラフから、\(V=3[V]\)

\(R=1Ω\)のとき、
\(i_L=3\left( 1-e^{-\frac{1}{L}t}\right) \)

\(R=2Ω\)のとき、
\(i_L=1.5\left( 1-e^{-\frac{2}{L}t}\right) \)

よって、\(R=2Ω\)の時の\(i_L\)は、次の二つのことがわかります。
(a)　1.5Vに収束する
(b)　\(R=1\)のグラフよりも時定数が短くなる　⇒　グラフが早く立ち上がる

(a)から、1.5Vに収束するグラフは(4)と(5)のみです。
\(R=1Ω\)のグラフと比較して、(4)のグラフは立ち上がりが早く、(5)のグラフは立ち上がりが遅いです。

以上より、\(R=2Ω\)のときの\(i_L\)のグラフは(4)です。

　

　

出典元

一般財団法人電気技術者試験センター　（https://www.shiken.or.jp/index.html）
令和３年度　第三種電気主任技術者試験　理論科目Ａ問題問１０

参考書