概要
電束密度\(D\)と、電気力線\(E\)が、誘電率\(ε\)の違いによってどのように変化するかを問う問題です。
電束・電気力線に関する基本的な事を抑えていれば回答できます。
キーワード
コンデンサの並列接続、比誘電率、電束の総数、電束密度\(D[C/m^2]\)、電界強度\(E[V/m]\)
問題
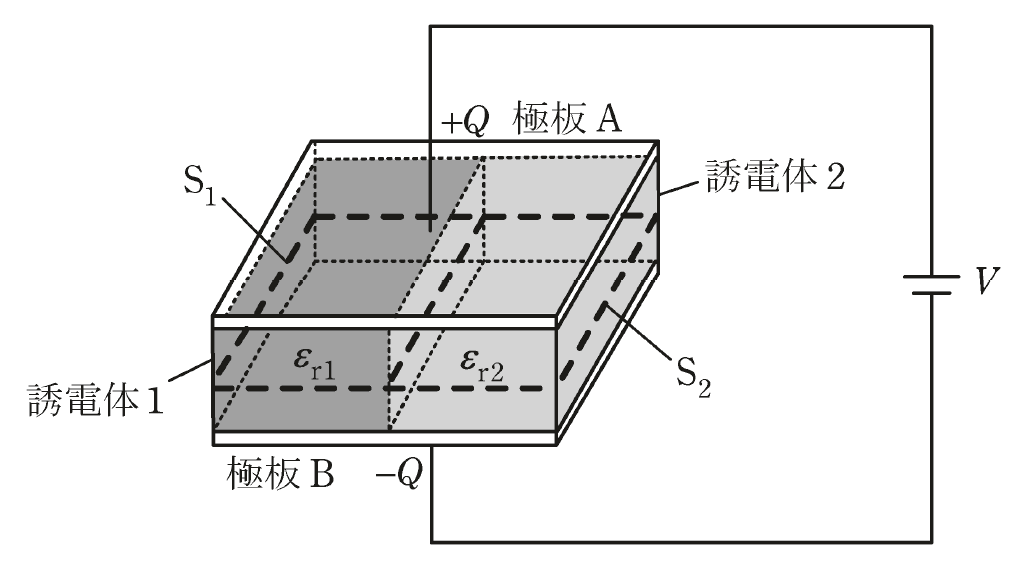
図のように、同じ寸法の直方体で誘電率の異なる二つの誘電体(比誘電率\(ε_{r1}\)の誘電体1と比誘電率\(ε_{r2}\)の誘電体2)が平行板コンデンサに充填されている。
極板間は一定の電圧\(V[V]\)に保たれ、極板Aと極板Bにはそれぞれ\(+Q[C]\)と\(-Q[C]\)(\(Q>0\))の電荷が蓄えられている。
誘電体1と誘電体2は平面で接しており、その境界面は極板に対して垂直である。
ただし、端効果は無視できるものとする。
この平行板コンデンサにおいて、極板A,Bに平行な誘電体1、誘電体2の断面をそれぞれ面\(S_1\)、面\(S_2\)(面\(S_1\)と面\(S_2\)の断面積は等しい)とすると、面\(S_1\)を貫く電気力線の総数(任意の点の電気力線の密度は、その点での電界の大きさを表す)は、面\(S_2\)を貫く電気力線の総数のア倍である。
面\(S_1\)を貫く電束の総数は面\(S_2\)を貫く電束の総数のイ倍であり、面\(S_1\)と面\(S_2\)を貫く電束の数の総和はウである。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
| (1) | 1 | \(\displaystyle \frac{ε_{r1}}{ε_{r2}}\) | Q |
| (2) | 1 | \(\displaystyle \frac{ε_{r1}}{ε_{r2}}\) | \(\displaystyle \frac{Q}{ε_r1}+\frac{Q}{ε_r2}\) |
| (3) | 1 | \(\displaystyle \frac{ε_{r2}}{ε_{r1}}\) | \(\displaystyle \frac{Q}{ε_r1}+\frac{Q}{ε_r2}\) |
| (4) | \(\displaystyle \frac{ε_{r2}}{ε_{r1}}\) | 1 | \(\displaystyle \frac{Q}{ε_r1}+\frac{Q}{ε_r2}\) |
| (5) | \(\displaystyle \frac{ε_{r2}}{ε_{r1}}\) | 1 | Q |
答え
(1)
要点整理
平行平板コンデンサの電界の強さE[V/m]
平行平板コンデンサの電界の強さEは次式で表されます。
\(\displaystyle E=\frac{Q}{ε_rε_0S}\)
\(\displaystyle E=\frac{Q}{ε_rε_0S}\) の式中の電荷\(Q[C]\)は、コンデンサの誘電率\(ε[F/m]\)によって変動します。
誘電率\(ε\)が違うコンデンサの比較をするような問題の場合、この式をそのまま適用すると誤答となりますので、考え方としては重要な式ですが、使う機会は少ないかもしれません。
\(Q[C]\)の電荷が出す電気力線の本数は、
\(N=\frac{Q}{ε}[本]\)です。
電界の強さ\(E[V/m]\)は、電気力線の本数の密度と等しいので、次式で表されます。
\(\displaystyle E=\frac{N}{S}=\frac{Q}{εS}\)
誘電率\(ε\)、比誘電率\(ε_r\)、真空の誘電率\(ε_0\)の関係は、
\(ε=ε_rε_0\)なので、
\(\displaystyle E=\frac{Q}{ε_rε_0S}\)
となります。
極板上の電荷Q[C]
極板上に蓄えられる電荷\(Q[C]\)は、静電容量\(C[F]\)、電圧\(V[V]\)としたとき、次式で表されます。
\(Q=CV\) ………①
電荷\(Q[C]\)は、コンデンサの静電容量\(C=ε\frac{S}{d}\)であることから、次式で表されます。
\(Q=ε\frac{S}{d}V\) ………②
コンデンサの誘電率\(ε[F/m]\)、コンデンサの極板面積\(S[m^2]\)、コンデンサの極板間距離\(d[m]\)、電圧\(V[V]\)です。
電界と電圧の関係
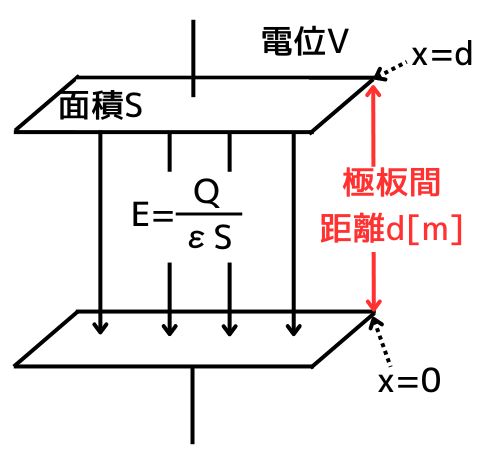
電界の強さ\(E[V/m]\)と、電位\(V[V]\)の関係は、極板間距離を\(d[m]\)とした時、次式で表されます。
\(V=Ed\)
\(V=Ed\)
この式は、平行平板コンデンサの問題で、回答する際にほぼ必ず使う式です。
最も重要な式と言っても良いので、必ず覚えましょう。

\(V=Ed\)を導出します。
電位\(V[V]\)は、\(1[C]\)の電荷を基点から対象点へ動かすときの仕事です。
基点はコンデンサの上端で\(d[m]\)
対象点はコンデンサの下端で\(0[m]\)
としたとき、電界の強さ\(E\)と電位\(V\)の関係は次のように表されます。
\(\displaystyle V=-\int_d^0E・dr=-\int_d^0\frac{Q}{εS}dr=-\frac{Q}{εS}[r]_d^0=\frac{Q}{εS}d=Ed\)
以上より、\(V=Ed\)が導出できました。
また、電界の強さ\(E\)の式から、電荷・静電容量・電圧の関係式を代入することでも導き出せます。
電界の強さ : \(E=\frac{Q}{εS}\) ………①
電荷・静電容量・電圧の関係式 : \(Q=CV\) ………②
コンデンサの静電容量 : \(C=ε\frac{S}{d}[F]\) ………③
①式に②・③式を代入すると、
\(\displaystyle E=\frac{Q}{εS}=C\frac{V}{εS}=\frac{εS}{d}・\frac{V}{εS}=\frac{V}{d}\)
よって、\(\displaystyle E=\frac{V}{d}\)が導き出せました。
平行平板コンデンサの電界の電束密度D
電束密度\(D[C/m^2]\)は、電荷(電束)\(Q[C]\)の密度です。
電束密度\(D[C/m^2]\)は、極板面積\(S[m^2]\)、電荷(電束)\(Q[C]\)としたとき、次式で表されます。
\(\displaystyle D=\frac{Q}{S}[C/m2]\)
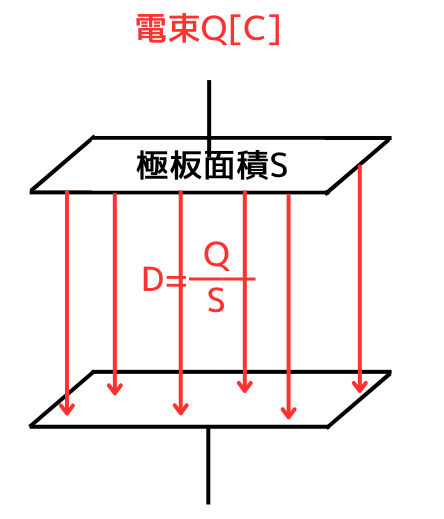
平行平板コンデンサにおいて、コンデンサの電束は、極板間のみを通りますので、電束を出す極板からどんなに距離が離れても面積\(S[m^2]\)は変わりません。
したがって、面積\(S[m^2]\)は、極板の面積Sとなります。
そのため、コンデンサの電束密度Dは、極板面積\(S[m^2]\)としたとき、
\(\displaystyle D=\frac{Q}{S}[C/m^2]\)
となります。
電束Q[C]・電束密度D[C/m2]・電気力線の本数N[本]・電界の強さE[V/m]の関係
電束密度\(D[C/m^2]\)と電界の強さ\(E[V/m]\)の関係式は、誘電率\(ε[F/m]\)を使って次式で表されます。
\(D=εE\)
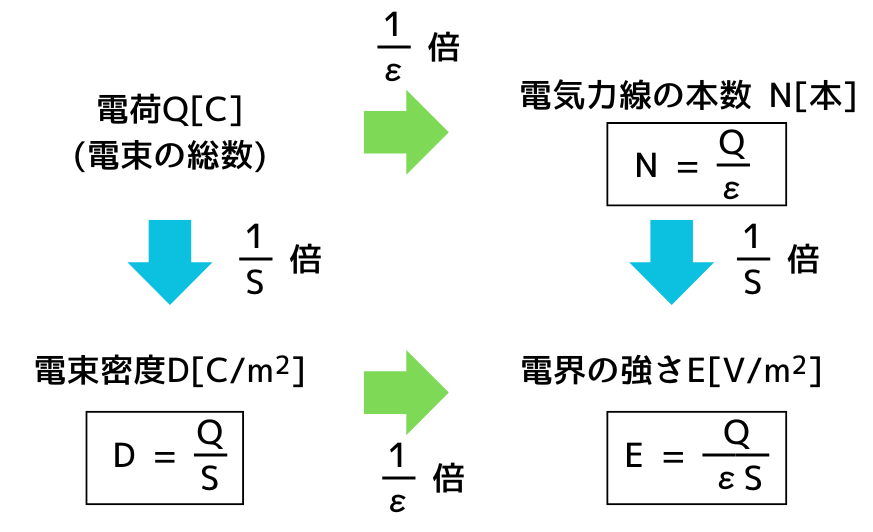
下記4つの関係をまとめて示すと図のようになります。
・電束\(Q[C]\)
・電気力線の本数\(N[本]\)
・電束密度\(D[C/m^2]\)
・電界の強さ\(E[V/m]\)
回答解説
アの回答
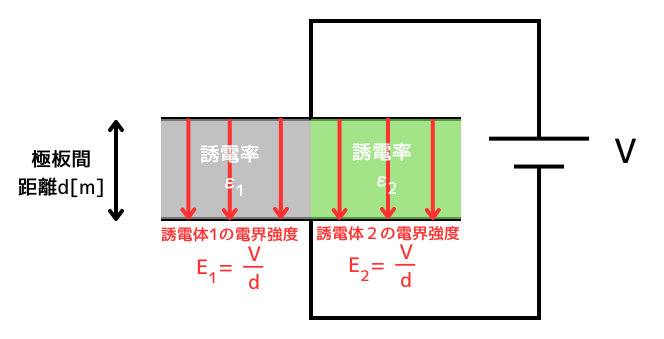
二つの誘電体は、「誘電体1と誘電体2は平面で接しており、その境界面は極板に対して垂直である」という設問の条件から、誘電体1と誘電体2は電源に対して並列接続されているとみなせます。そのため、誘電体1、誘電体2それぞれに電圧\(V[V]\)が印加されていると考えられます。
\(V=Ed\) ⇔ \(E=\frac{V}{d}[V/m]\) の関係式から、
\(\displaystyle E_1=\frac{V}{d}\) ………①
\(\displaystyle E_2=\frac{V}{d}\) ………②
であることがわかります。
電界の強さ\(E[V/m]\)は、電気力線の密度であるので、電気力線の総数N[本]は、
\(N=ES\)の式で求められます。
\(\displaystyle N_1=E_1S_1=\frac{S_1V}{d}\) ………③
\(\displaystyle N_2=E_2S_2=\frac{S_2V}{d}\) ………④
③÷④式かつ、\(S_1=S_2\)から、
\(\displaystyle \frac{N_1}{N_2}=1\)
したがって、(ア)は、1です。
イの回答
電束密度\(D[C/m^2]\)と、電界の強さ\(E[V/m]\)の関係式は、次式で表されます。
\(D=εE\) ………⑤
⑤式に、①・②式の電界の強さと、各誘電体の誘電率\(ε_{r1}\)、\(ε_{r2}\)を代入すると、
\(\displaystyle D_1=ε_1E_1=ε_{r1}\frac{V}{d}\) ………⑥
\(\displaystyle D_2=ε_2E_2=ε_{r2}\frac{V}{d}\) ………⑦
面\(S_1\)を貫く電束の総数を\(Q_1[C]\)
面\(S_2\)を貫く電束の総数を\(Q_2[C]\)とすると、
\(\displaystyle Q_1=D_1S_1=\frac{ε_{r1}S_1V}{d}\) ………⑧
\(\displaystyle Q_2=D_2S_2=\frac{ε_{r2}S_2V}{d}\) ………⑨
⑧÷⑨式かつ、\(S_1=S_2\)から、
\(\displaystyle \frac{Q_1}{Q_2}=\frac{ε_{r1}}{ε_{r2}}\)
したがって、(イ)は、\(\frac{ε_{r1}}{ε_{r2}}\)です。
ウの回答
面\(S_1\)と面\(S_2\)を貫く電束の数の総和は、極板A、Bに溜まった電荷(電束)であるため、\(Q[C]\)です。
なお、(イ)の設問で求めた\(Q_1\)と\(Q_2\)と、コンデンサ全体の電束の数の総和の関係は、
\(Q=Q_1+Q_2\)
です。
したがって、(ウ)は、\(Q[C]\)です。
以上より、(1)が答えとなります。
出典元
一般財団法人 電気技術者試験センター
令和3年度第三種電気主任技術者試験 理論科目A問題問1
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント