概要
分巻電動機と、直巻電動機のトルク特性を問う論説問題す。
各種電動機の速度特性とトルク特性は基本的な内容なので、確実に回答できるようになっておきたい問題です。
キーワード
直流機、分巻電動機、直巻電動機、トルク特性
問題
次の文章は、直流電動機に関する記述である。
ただし、鉄心の磁気飽和、電機子反作用、電機子抵抗やブラシの接触による電圧降下は無視できるものとする。
分巻電動機と直巻電動機はいずれも界磁電流を電機子と同一の電源から供給できる電動機である。
分巻電動機において端子電圧と界磁抵抗を一定にすれば、負荷電流が増加したとき界磁磁束は \(\fbox{(ア)}\) 、トルクは負荷電流に \(\fbox{(イ)}\) する。
直巻電動機においては負荷電流が増加したとき界磁磁束は \(\fbox{(ウ)}\) 、トルクは負荷電流の \(\fbox{(エ)}\) に比例する。
| (ア) | (イ) | (ウ) | (エ) | |
|---|---|---|---|---|
| (1) | 一定で | 比例 | 増加し | 2乗 |
| (2) | 一定で | 反比例 | 一定で | 1乗 |
| (3) | 一定で | 比例 | 一定で | 2乗 |
| (4) | 増加し | 反比例 | 減少し | 1乗 |
| (5) | 増加し | 反比例 | 増加し | 2乗 |
答え
(1)
解説テキスト リンク
回答解説
\(\fbox{(ア)}\)・\(\fbox{(イ)}\)
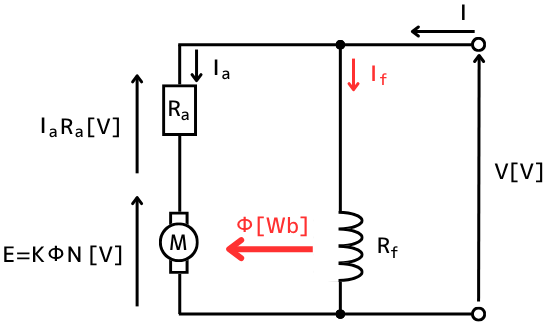
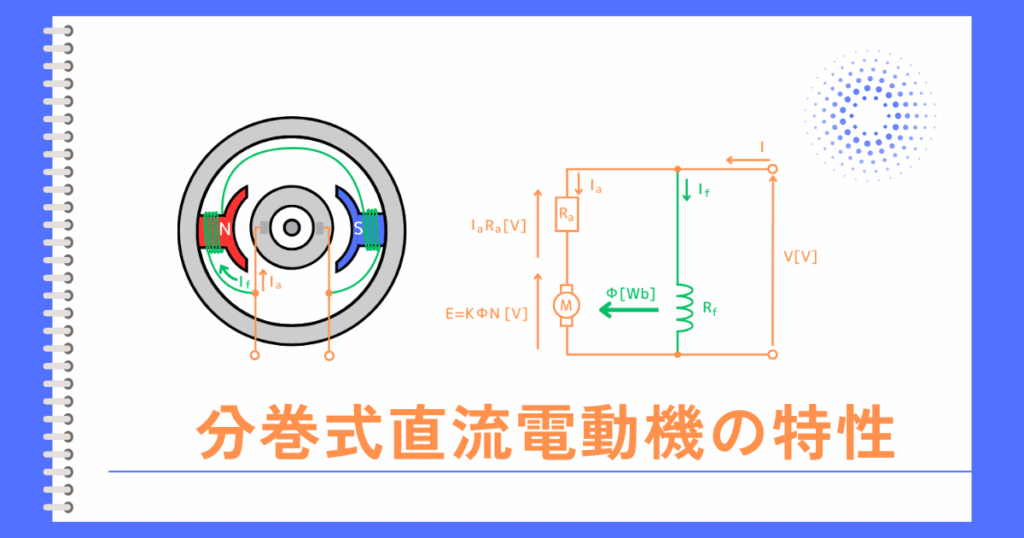
分巻電動機の回路は
負荷電流\(I_a\)が流れる主回路と、
界磁電流\(I_f\)が流れる界磁回路に分かれています。
端子電圧\(V\)と界磁抵抗\(R_f\)を一定にすると、オームの法則から界磁電流\(I_f\)は一定です。
界磁磁束\(\Phi\)は界磁電流\(I_f\)に比例します。
分巻電動機では、負荷電流が変化しても界磁電流が一定なので、界磁磁束も(ア)一定です。
トルクの式は、\(T=K_T \Phi I_a\)です。
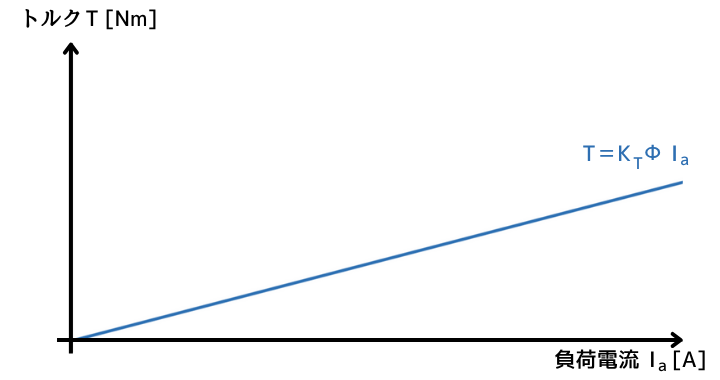
\(K_T\)は比例定数です。
比例定数は常に一定です。
\(\Phi\)は、界磁磁束です。
設問(ア)から、\(\Phi\)は一定です。
\(I_a\)は、負荷電流です。
以上より、トルクは負荷電流に(イ)比例することがわかります。
\(\fbox{(ウ)}\)・\(\fbox{(エ)}\)
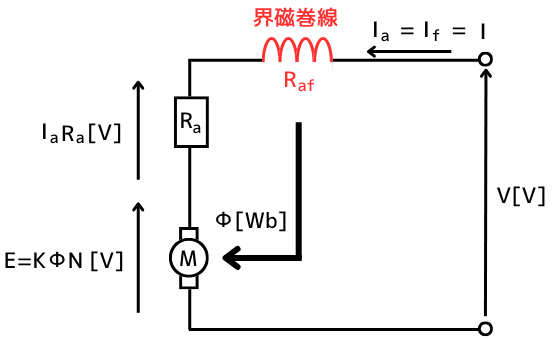
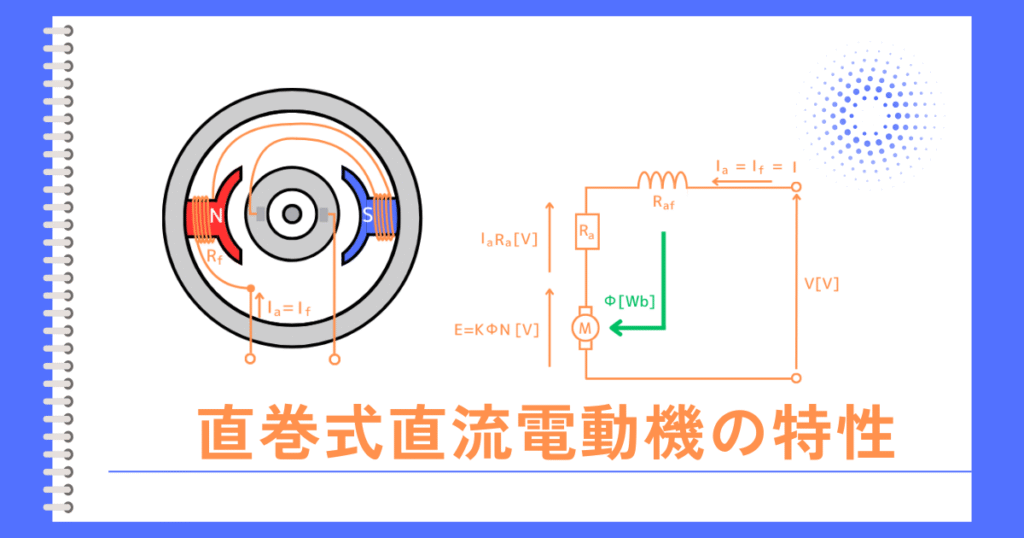
直巻電動機の回路は
界磁巻線と主回路が直列接続されているため、界磁巻線にも負荷電流\(I_a\)が流れます。
このことから、負荷電流\(I_a\)が増加したとき、(ウ)界磁磁束は増加することがわかります。
トルクの式は、\(T=K_T \Phi I_a\)です。
界磁磁束\(\Phi\)は、界磁電流\(I_f\)に比例します。
直巻電動機は、『 負荷電流\(I_a=\)界磁電流\(I_f\) 』であることから、
界磁磁束\(\Phi\)は、負荷電流\(I_a\)に比例して大きくなることがわかります。
比例定数\(k\)を使って界磁磁束\(\Phi\)を表すと、
\(\Phi = kI_a\)
となります。これをトルクの式に代入すると、
\(T=K_T k I_a^2\)
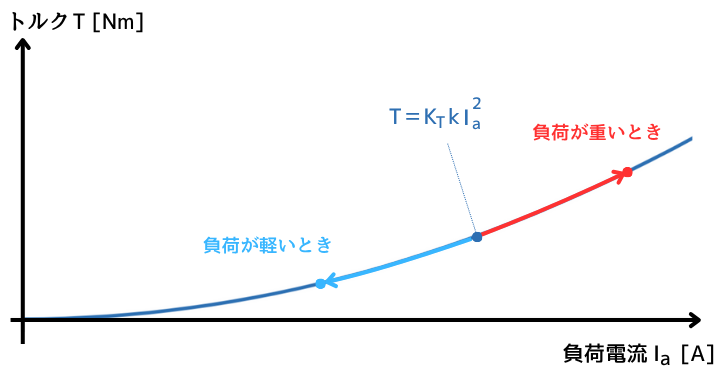
\(K_T\)、\(k\)は、比例定数なので一定です。
\(I_a\)は、負荷電流です。
したがって、トルクは負荷電流の二乗に比例します。
以上より、トルクは負荷電流の(エ)二乗に比例することがわかります。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和3年度 第三種電気主任技術者試験 機械科目問題問1
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
電験三種の領域をずっと超えた先の話を9割方しているので、電験三種の勉強の参考書としての購入はおすすめしません。
直流電動機について、ありとあらゆる事を書き記していった一冊です。
この本より詳しい本は少ないと思いますので、直流電動機の設計を学ぶ人に取っては良い本かと思われます。
感覚的には、研究論文化する内容ではないけど、後世には残しておきたいと思ったことをまとめたというような感じでしょうか。
文章の癖は強いので、もし買う場合はサンプルを読んでから購入することを推奨します。







コメント