概要
RLC回路を直列接続したとき、並列接続したときの、各抵抗、コイル、コンデンサの電圧・電流の位相を問う問題です。
各素子の位相特性について理解をしている場合、計算するまでも無く解答できますが、地道に計算しても比較的簡単に導出できます。
RLC回路は計算量が多くて取っ付き難い問題が多いため、その印象から避けたくなりますが、実際に取り組んでみると、あっさり解ける問題です。
キーワード
交流回路、RLC回路、位相
問題
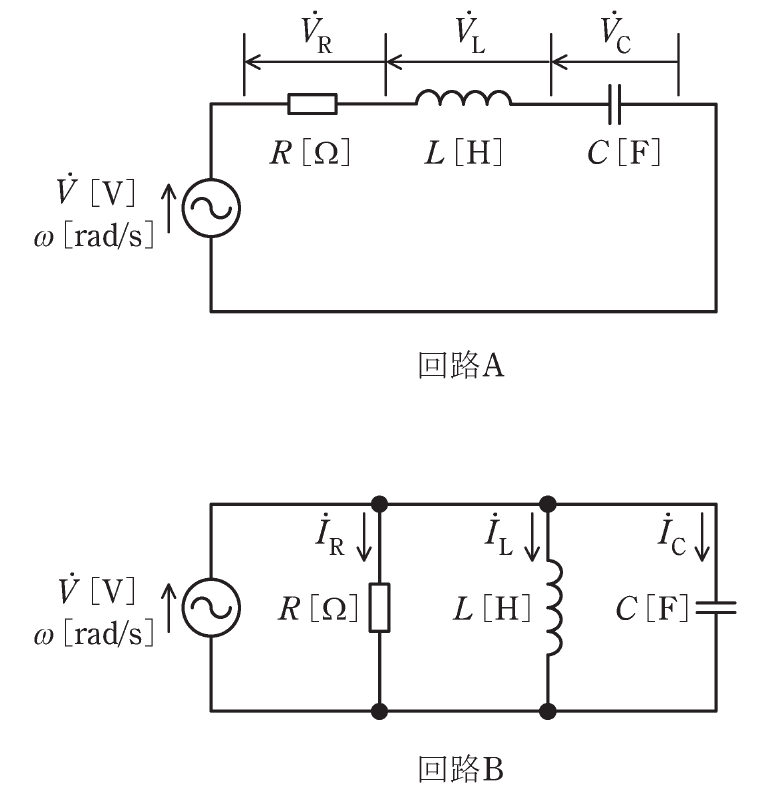
図のように、\(R[Ω]\)の抵抗、インダクタンス\(L[H]\)のコイル、静電容量\(C[F]\)のコンデンサと電圧\(\dot{V}[V]\)、角周波数\(ω[rad/s]\)の交流電源からなる二つの回路AとBがある。
両回路においてそれぞれ\(ω^2LC=1\)が成り立つとき、各回路における図中の電圧ベクトルと電流ベクトルの位相の関係として、正しいものの組合せを(1)~(5)のうちから一つ選べ。
ただし、ベクトル図における進み方向は反時計回りとする。
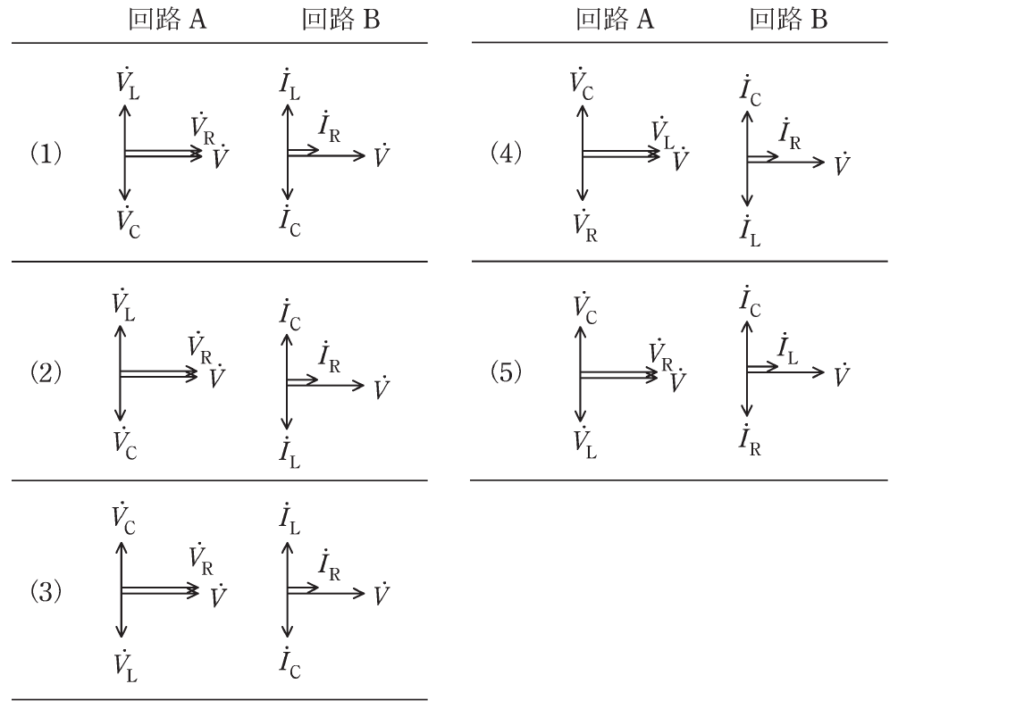
答え
(2)
解説テキスト リンク
回答解説
抵抗、コイル、コンデンサの各々の位相特性を理解している場合は楽に答えられますが、理解していない場合でも計算式から回答を十分導き出せます。
【解答1】各素子の位相特性を理解している場合の解答
RLC直列接続回路、並列接続回路の抵抗、コイル、コンデンサの位相特性を理解している場合は、簡単に解答できます。
RLC直列接続回路
①\(ω^2LC=1\)の条件から、回路を流れる電流の位相は、電圧源\(\dot{V}\)の位相と同じ。
②抵抗の電圧\(\dot{V_R}\)の位相は、電流の位相と同じ。
③コイルの電圧\(\dot{V_L}\)の位相は、電流の位相よりも90°進む。
④コンデンサの電圧\(\dot{V_C}\)の位相は、電流の位相よりも90°遅れる。
RLC並列接続回路
①\(ω^2LC=1\)の条件から、回路を流れる電流の位相は、電圧源\(\dot{V}\)の位相と同じ。
②抵抗の電流\(\dot{I_R}\)の位相は、電圧源の位相と同じ。
③コイルの電流\(\dot{I_L}\)の位相は、電圧源の位相よりも90°遅れる。
④コンデンサの電流\(\dot{I_C}\)の位相は、電流の位相よりも90°進む。
以上のことをまとめると、(2)が解となります。
【解答2】計算して導き出す
解答の流れ
回路Aの解答
① インピーダンス\(\dot{Z}\)を導出する
② 回路を流れる電流\(\dot{I}\)を求める
③ オームの法則から\(V_R\)を求める
④ オームの法則から\(V_L\)を求める
⑤ オームの法則から\(V_C\)を求める
⑥ まとめ
回路Bの解答
⑦ オームの法則から\(I_R\)を求める
⑧ オームの法則から\(I_L\)を求める
⑨ オームの法則から\(I_C\)を求める
⑩ まとめ
結論
回路Aの解答
① インピーダンス\(\dot{Z}\)の式を導出する
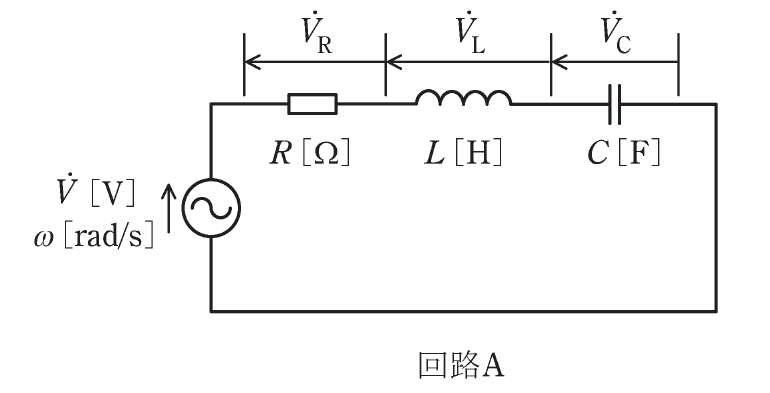
RLC直列接続回路のインピーダンス\(\dot{Z}\)は、
\(\displaystyle \dot{Z}=R+jωL+\frac{1}{jωC}\)
\(\displaystyle \dot{Z}=R+j(ωL-\frac{1}{ωC})\)
\(ω^2LC=1\)の条件から、
\(ω^2LC=1\) ⇔ \(ωL=\frac{1}{ωC}\)
これを\(\dot{Z}\)の式に代入すると、
\(\dot{Z}=R\)
となります。
したがって、回路のインピーダンス\(\dot{Z}\)は、抵抗成分のみとなります。
② 回路を流れる電流\(\dot{I}\)を求める
オームの法則から、
\(\dot{I}=\frac{\dot{V}}{\dot{Z}}=\frac{\dot{V}}{R}\)
式中にjの虚数項がないので、回路中を流れる電流\(\dot{I}\)は、電圧源の電圧\(\dot{V}\)と同位相となります。
③ オームの法則から\(V_R\)を求める
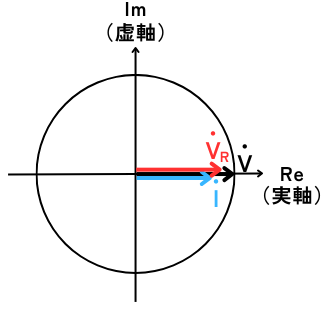
\(\dot{V_R}=R\dot{I}\)
であるため、\(\dot{V_R}\)と\(\dot{I}\)は同位相です。
\(\dot{I}\)は、電源電圧\(\dot{V}\)と同位相であるため、\(\dot{V_R}\)は\(\dot{V}\)と同位相となります。
④ オームの法則から\(V_L\)を求める
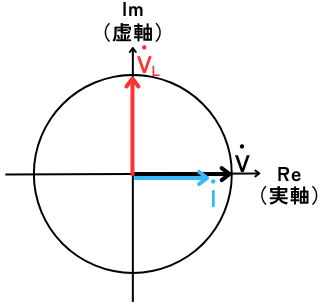
\(\dot{V_L}=jωL\dot{I}\)
です。虚数\(j\)は、位相が90°進んでいることを表すため、
\(\dot{V_L}\)は、\(\dot{I}\)よりも位相が90°進んでいます。
したがって、\(\dot{V_L}\)は、\(\dot{V}\)よりも位相が90°進んでいます。
⑤ オームの法則から\(V_C\)を求める
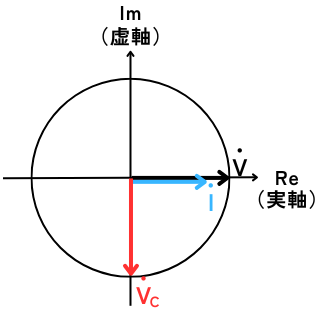
\(\dot{V_C}=\frac{\dot{I}}{jωC}=-j\frac{\dot{I}}{ωC}\)
です。虚数\(-j\)は、位相が90°遅れていることを表すため、
\(\dot{V_C}\)は、\(\dot{I}\)よりも位相が90°遅れています。
したがって、\(\dot{V_C}\)は、\(\dot{V}\)よりも位相が90°遅れています。
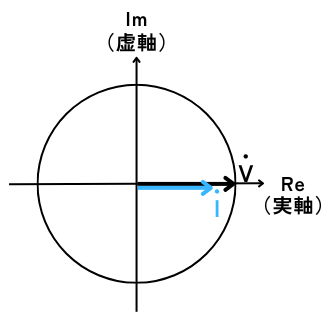
⑥ まとめ
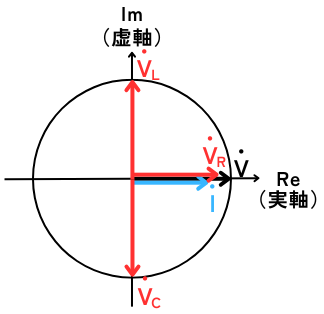
\(V_R\)、\(V_L\)、\(V_C\)をまとめると、
左図のようになります。
回路Bの解答
⑦ オームの法則から\(I_R\)を求める
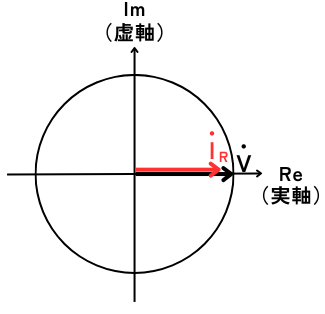
オームの法則から、
\(\dot{I_R}=\frac{\dot{V}}{R}\)
式中にjの虚数項がないので、回路中を流れる電流\(\dot{I_R}\)は、電圧源の電圧\(\dot{V}\)と同位相となります。
⑧ オームの法則から\(I_L\)を求める
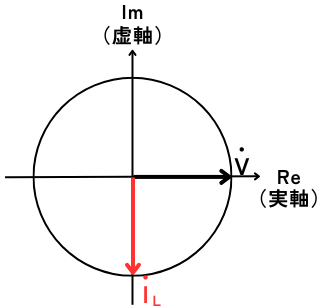
オームの法則から、
\(\displaystyle \dot{I_L}=\frac{\dot{V}}{jωL}=-j\frac{\dot{V}}{ωL}\)
式中に-jの虚数項があるので、回路中を流れる電流\(\dot{I_L}\)は、電圧源の電圧\(\dot{V}\)よりも位相が90°遅れています。
⑨ オームの法則から\(I_C\)を求める
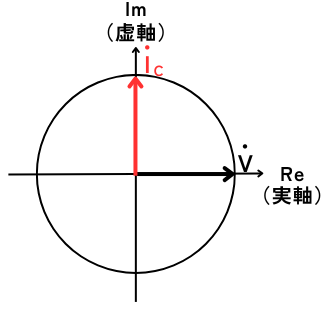
オームの法則から、
\(\displaystyle \dot{I_C}=jωC\dot{V}\)
式中にjの虚数項があるので、回路中を流れる電流\(\dot{I_C}\)は、電圧源の電圧\(\dot{V}\)よりも位相が90°進んでいます。
⑩ まとめ
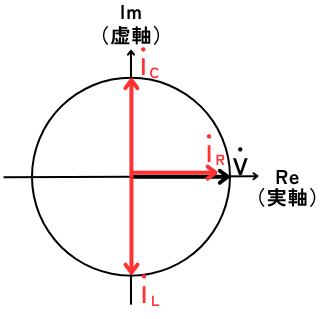
\(I_R\)、\(I_L\)、\(I_C\)をまとめると、
左図のようになります。
結論
以上、⑥・⑩より、(2)が答えとわかります。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和2年度 第三種電気主任技術者試験 理論科目A問題問9
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント