フィードバック(帰還)とは
フィードバック(帰還)とは、オペアンプの出力信号の一部を、入力信号に戻し、入力と出力を比較することで、必要な出力になるように調整・制御する方法です。
フィードバックには、ポジティブフィードバック(正帰還)と、ネガティブフィードバック(負帰還)の2種類のフィードバックがあります。
本ページでは、ネガティブフィードバックについて解説します。
ネガティブフィードバック(負帰還)
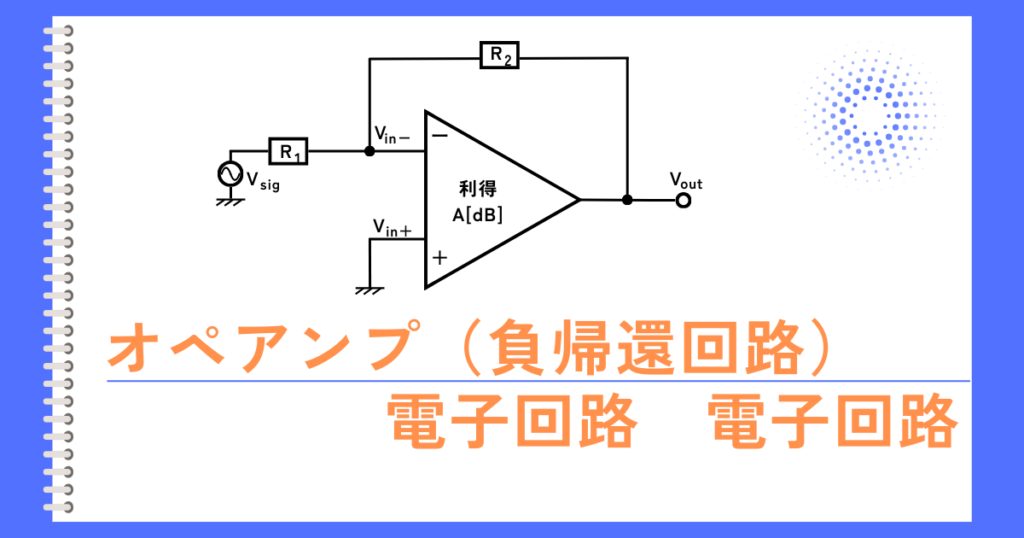
ネガティブフィードバックとは、出力電圧\(V_{out}\)を、反転入力\(V_{in-}\)に戻すようにした回路です。
オープンループ(フィードバックしない回路)
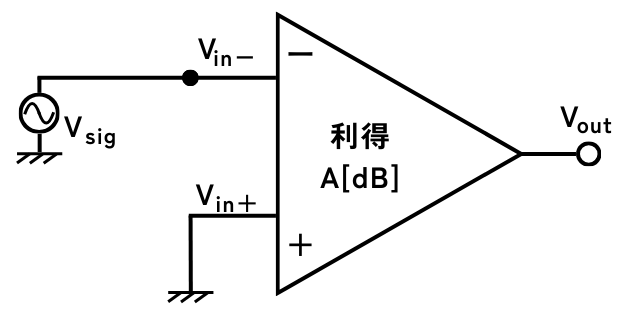
オペアンプ単体でフィードバックしていない回路をオープンループと呼び、オープンループの利得(ゲイン)をオープンループゲインと呼びます。
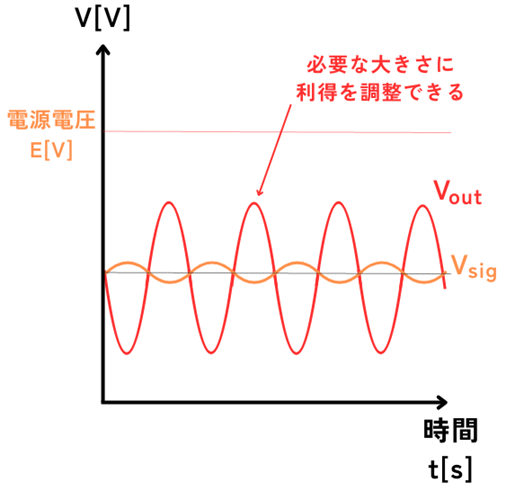
オペアンプの利得は\(40[dB]\)程度と低くても\(10^2=100\)倍、\(100[dB]\)になると\(10^5=100000倍\)です。
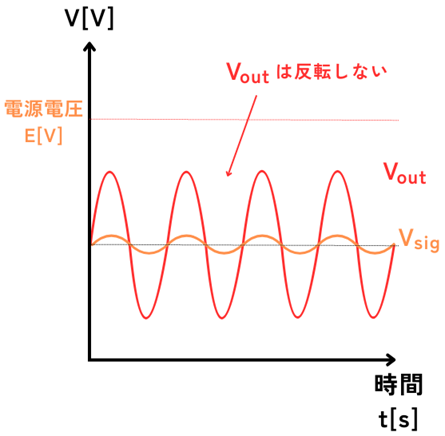
\(100[dB]\)の大きな利得は、入力信号電圧\(V_{sig}\)の振幅が仮に\(1mV\)程度だったとすると、\(100V\)まで増幅することができます。
オペアンプは電源電圧よりも大きな電圧にすることはできないので、出力信号波形は増幅しすぎて潰れてしまいます。
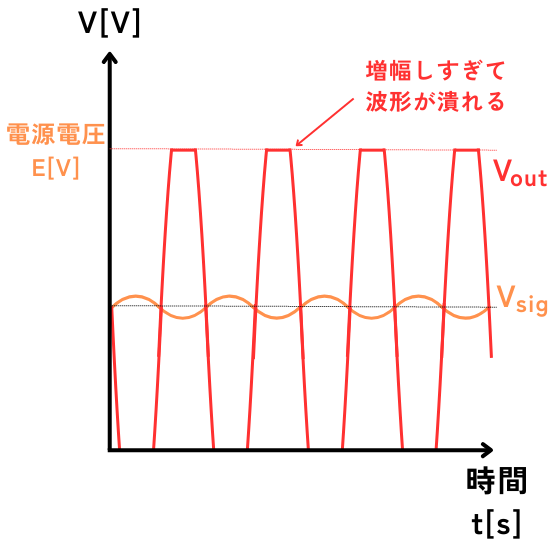
このことから、オープンループを使って回路設計をすることは難しい(不可能)です。
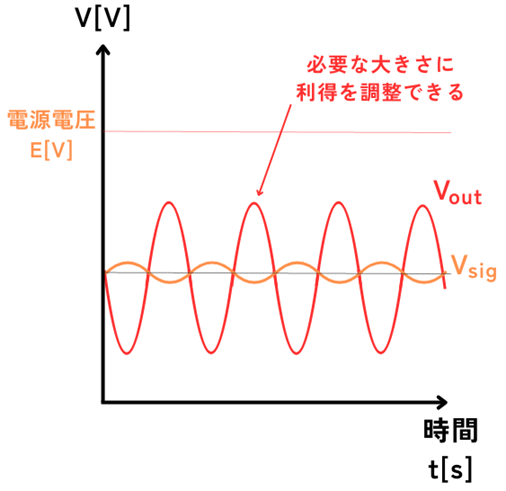
そこで、ネガティブフィードバックを利用することで、利得を必要な値に設定することができるので、安定した動作ができます。
クローズドループ
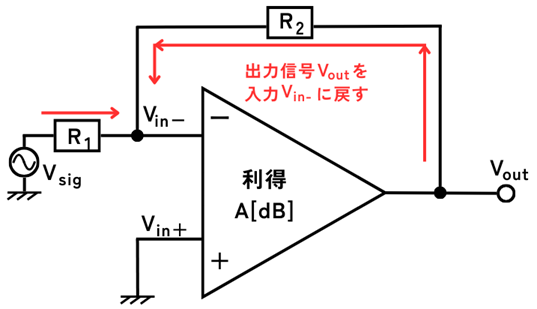
図のように\(V_{out}\)と\(V_{in-}\)を接続することで、ネガティブフィードバックしている回路をクローズドループと呼びます。
オペアンプの出力電圧\(V_{out}[V]\)を
\(\displaystyle V_{out}=-\frac{R_2}{R_1}V_{sig}[V]\)
に調整することができます。
\(R_1\)と\(R_2\)の大きさでクローズドループゲインを調整することができるため、出力信号電圧\(V_{out}\)を必要な大きさに簡単に調整できます。
フィードバックは、波形の大きさの調整だけに限らず、抵抗、コンデンサ等のつなげる素子や、接続方法によって様々な機能を持たせることができます。
フィードバック回路の計算
イマジナリーショート
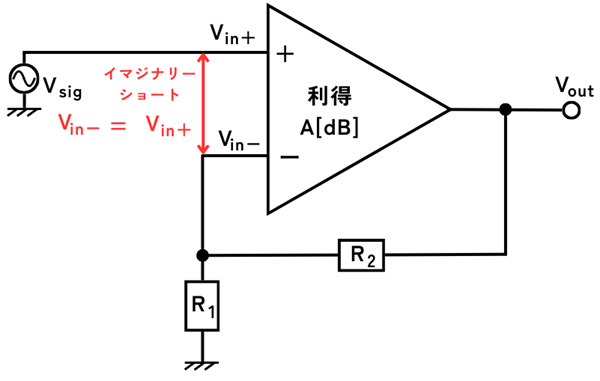
ネガティブフィードバックの回路の計算をするときは、反転入力の\(V_{in-}\)と、非反転入力\(V_{in+}\)の電圧が同電位(ショート状態)であると見なして計算することをイマジナリーショートと呼びます。実際にはショートしていませんが、仮想的なショート状態ということで、この名前がついています。
イマジナリーショートの理由
ネガティブフィードバック回路を、イマジナリーショートを使って計算する理由について示していきます。次の図は、反転入力電圧\(V_{in-}\)と出力電圧\(V_{out}\)が短絡接続され、\(V_{in-}=V_{out}\)となって同じになる回路です。(ユニティゲインバッファ回路と呼ばれる回路です)
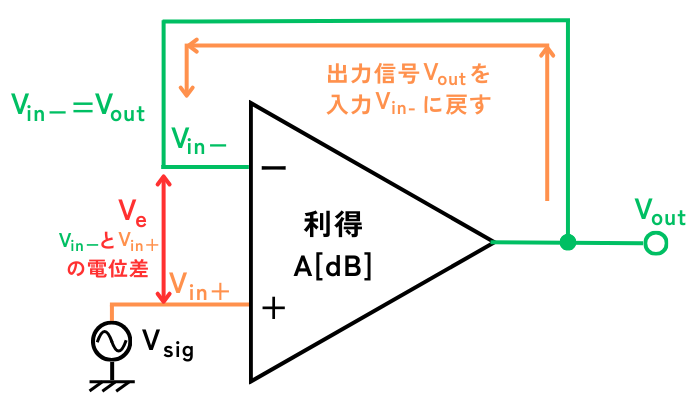
非反転入力電圧\(V_{in+}\)に、\(0V\)から、一瞬で\(1V\)になるステップ入力がされたとします。
\(V_{in-}\)と\(V_{in+}\)の電位差を\(V_e\)とすると、\(V_e=V_{in+}-V_{in-}\)です。
このとき、出力\(V_{out}\)は、
\(V_{out}=AV_e=A(V_{in+}-V_{in-})\) …①
かつ
\(V_{out}=V_{in-}\) …②
です。
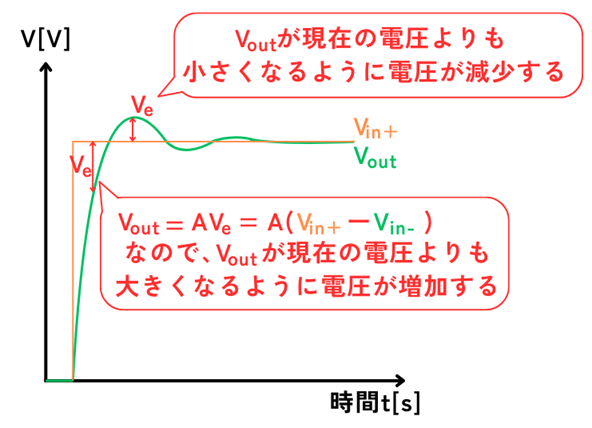
(1)\(V_{in+}>(V_{in-}=V_{out})\)のとき
①式から\(V_{out}\)が大きくなるように電圧が調整されます。
そのことにより、\(V_{in+}\)と、\(V_{out}\)の電圧が近づきます。
(2)\((V_{in-}=V_{out})>V_{in+}\)のとき
①式から\(V_{out}\)が小さくなるように電圧が調整されます。
そのことにより、\(V_{in+}\)と、\(V_{out}\)の電圧が近づきます。
(1)・(2)のどちらの場合においても、\(V_{out}\)が\(V_{in+}\)に近づくように調整されていった結果、\(V_{in+}=V_{out}\)となります。
\(V_{out}=V_{in-}\)なので、\(V_{in+}=V_{in-}\)となり、\(V_{in+}\)と\(V_{in-}\)は仮想的にショートされた状態とみなすことができます。
イマジナリーショートの理由を数式的に示します。
\(V_{out}=V_{in-}\)
なので、
\(V_{out}=AV_e=A(V_{in+}-V_{in-})=AV_{in+}-AV_{out}\)
⇔ \((1+A)V_{out}=AV_{in+}\)
⇔ \(\displaystyle V_{out}=\frac{A}{1+A}V_{in+}\)
オペアンプの理想ゲインは\(A=∞[dB]\)なので、
\(\displaystyle \frac{A}{1+A}≒1\)となります。
したがって、\(V_{out}=V_{in+}\)となるので、\(V_{in-}=V_{in+}\)が成り立ちます。
以上より、\(V_{in-}\)と\(V_{in+}\)を同電位とみなす、イマジナリーショートの理由を示すことができました。
反転増幅回路
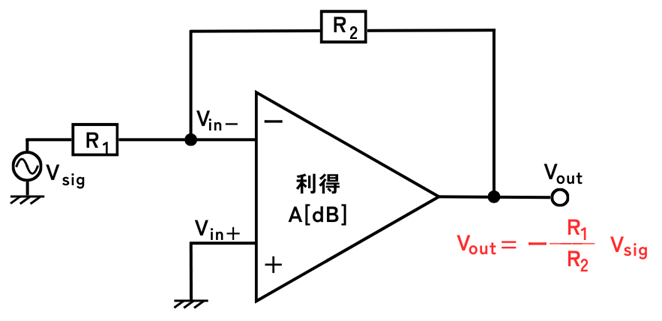
反転増幅回路は、入力信号\(V_{sig}\)を抵抗\(R_1\)を通して反転入力\(V_{in-}\)に接続し、出力端子を抵抗\(R_2\)を通して反転入力\(V_{in-}\)に接続します。
この時の出力は、次式で表され、抵抗\(R_1\)と\(R_2\)の比率によって電圧利得を調整することができます。
\(\displaystyle V_{out}=-\frac{R_2}{R_1}V_{sig}\)
出力信号の導出
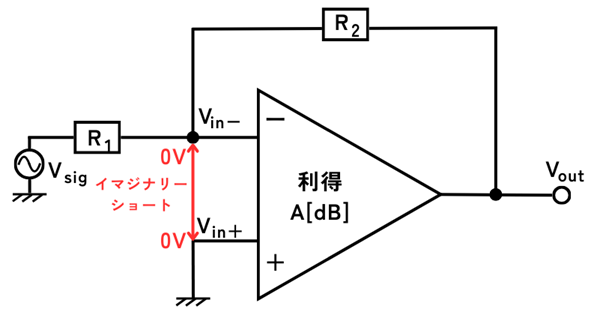
\(V_{in+}\)は、接地しているため\(0V\)です。
イマジナリーショートにより、
\(V_{in-}=V_{in+}=0V\)です。
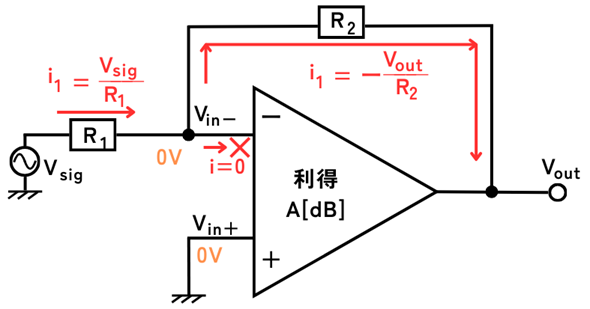
入力電圧信号源\(V_{sig}\)から\(V_{in-}\)に抵抗\(R_1\)を通って流れる電流\(i_1\)は、
\(\displaystyle i_1=\frac{V_{sig}}{R_1}\)…①
オペアンプの入力インピーダンスの理想特性は\(Z_{in}=∞\)なので、\(V_{in-}\)からオペアンプ内に電流は流れません。
したがって、\(V_{sig}\)から流れ込んできた\(i_1\)は、抵抗\(R_2\)を流れて全て出力端子\(V_{out}\)に流れます。
\(\displaystyle i_1=-\frac{V_{out}}{R_2}\)…②
①式=②式なので、
\(\displaystyle \frac{V_{sig}}{R_1}=-\frac{V_{out}}{R_2}\)
⇔ \(\displaystyle V_{out}=-\frac{R_2}{R_1}V_{sig}\)
出力信号\(V_{out}\)の式が導出できました。
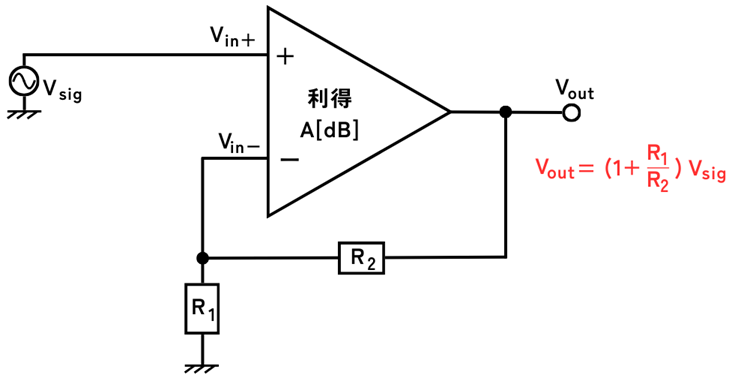
非反転増幅回路
非反転増幅回路は、入力信号\(V_{sig}\)を非反転入力\(V_{in+}\)に接続します。
出力端子\(V_{out}\)と、二つの抵抗\(R_1\)、\(R_2\)で分圧した電圧を反転入力\(V_{in-}\)に接続します。
この時の出力は、次式で表され、抵抗\(R_1\)と\(R_2\)の比率によって電圧利得を調整することができます。
\(\displaystyle V_{out}=(1+\frac{R_2}{R_1})V_{sig}\)
出力信号の導出
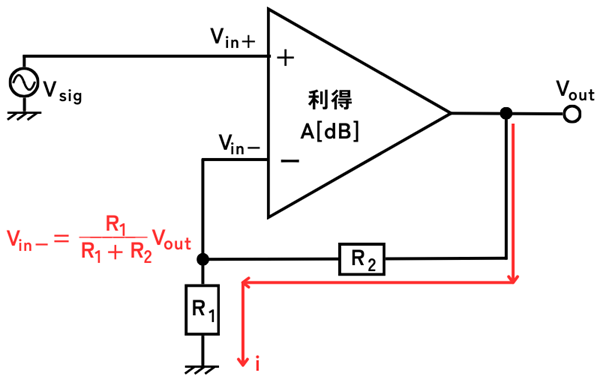
\(V_{in-}\)は、出力端子\(V_{out}\)から分圧した電圧が供給されますので
\(\displaystyle V_{in-}=\frac{R_1}{R_1+R_2}V_{out}\) …①
イマジナリーショートにより
\(V_{in-}=V_{in+}\)
\(V_{in+}\)は、入力信号\(V_{sig}\)が接続されるので、
\(V_{in+}=V_{sig}\)
したがって、
\(V_{in-}=V_{sig}\) …②
①式、②式から、
\(\displaystyle \frac{R_1}{R_1+R_2}V_{out}=V_{sig}\)
⇔\(\displaystyle V_{out}=(1+\frac{R_2}{R_1})V_{sig}\)
出力信号\(V_{out}\)の式が導出できました。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
コメント