関連公式一覧
抵抗\(R[Ω]\)と抵抗率\(ρ[Ω・m]\)の関係式
(\(S[m^2]\):面積、\(L[m]\):長さ)
\(\displaystyle R=ρ\frac{L}{S}[Ω]\)
コンダクタンス\(G\)と抵抗\(R\)関係式
\(\displaystyle G=\frac{1}{R}\)
コンダクタンス\(G\)と導電率\(σ\)の関係式
(\(S[m^2]\):面積、\(L[m]\):長さ)
\(\displaystyle G=σ\frac{S}{L}\)
導電率\(σ\)と抵抗率\(ρ\)の関係式
\(\displaystyle σ=\frac{1}{ρ}\)
抵抗温度係数を\(α\)と温度による抵抗の関係式
(\(t_1[℃]\)の時の抵抗値は\(R_{t1}\)、\(t_2[℃]\)の時の抵抗値は\(R_{t2}\))
\(R_{t2}=R_{t1}(1+α(t_2-t_1)\)
オームの法則の式
\(V=RI\)
消費電力の式
\(\displaystyle P=IV=I^2R=\frac{V^2}{R}[W]\)
消費電力とジュール熱の関係式
\(\displaystyle P=\frac{J}{t}[W]\)
⇔\(J=Pt[J]\)
電気回路
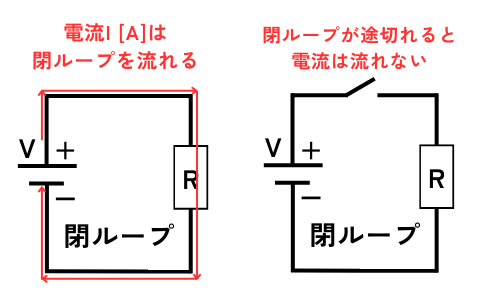
電気回路とは、例えば電池の+極から送り込まれた電流が電球等の負荷に流れ、電池の-極に戻るような電気的な道筋のことです。
電流の供給元の+極(電池等)から、負荷(電球等)を通り、供給元の-極に戻ることで形成されるループを閉ループといいます。
電気回路が動作するときは、アンテナのような一部例外を除き、必ず閉ループが形成されます。
電圧 V[V]
電流を流そうとするエネルギーを電圧といい、電圧が高いと電流は強く流れます。
電圧には、直流電圧と、交流電圧の二種類があります。
直流電圧は、常に一定の向きである電圧のことです。電流の向きも常に一定方向に供給します。
直流電圧を供給する物の代表例は電池です。電池の+極から出た電流が、電球などの様々な負荷を通って電池の-極に戻ることで直流回路を動作させます。
交流電圧は、一定周期で電圧の大きさや向きを変えることで、電流を流す量と方向を変化させる電圧のことです。この変化は正弦波状であるため、三角関数が切っても切り離せない存在です。
交流電圧を供給する物の代表例はコンセントです。
電流 I[A]
電流とは電荷の流れのことです。
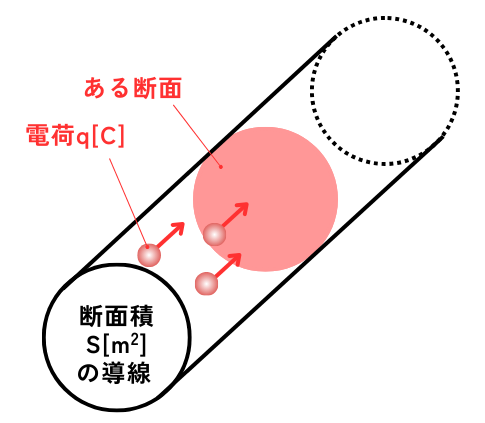
電流の大きさ
ある断面を\(t[s]\)間に\(q[C]\)の電荷が流れる時、\(I=\frac{q}{t}[A]\)です。
したがって、\(1[s]\)間に\(1[C]\)の電荷が流れるとき、\(I=1[A]\)となります。
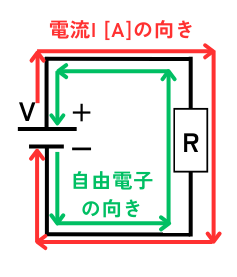
電流の向き
電流の向きは、正の電荷が移動する向きです。電池に閉ループをつなぐと、電流は+極から-極へ向かって流れます。
電気回路を流れる電荷は自由電子です。自由電子は負電荷であるため、電流とは逆に-極から+極へ向かって流れます。
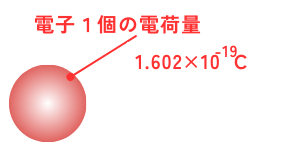
電気素量
1個の自由電子\(e\)の電荷量を電気素量と言います。
電気素量は、\(e\)の記号で表され、\(e[C]\)の大きさは、約\(1.602×10^{-19}[C]\)です。
抵抗 R[Ω]
電気抵抗とは、物質の電気の通りにくさを表す指標で、抵抗値が大きいほど電流は流れにくくなり、小さいほど流れやすくなります。
抵抗で消費された電力は、全て熱になります。
銅やアルミ等の金属は抵抗が低く、導体と呼ばれます。電流が流れても熱として損失する量が少ないため、電線として使用されます。
ゴム、ビニルやポリエチレン等の素材は、抵抗が非常に高く、電気を殆ど通さないため絶縁体と呼ばれます。電線を絶縁体で覆うことで、不要な箇所に電気が流れる漏電が起こることを防ぎます。
抵抗率ρ[Ω・m]
抵抗率\(ρ\)は、抵抗\(R\)の単位長さと単位断面積あたりの電気の流れにくさを示します。
比抵抗と呼ぶこともあります。
電線のような様々な長さ・太さがあるような材料に対して、どれくらいの長さのとき、どれくらいの太さの電線が必要だろうか?といった検討をするときに使用します。
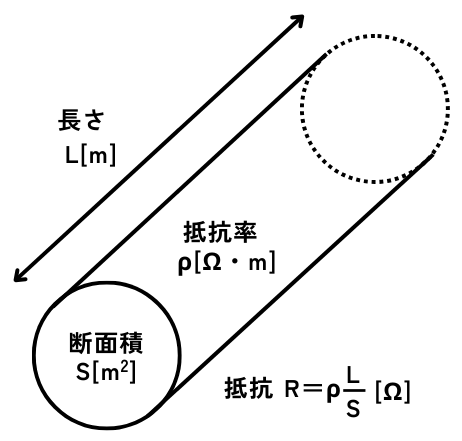
抵抗率\(ρ[Ω・m]\)と、抵抗\(R[Ω]\)の関係は、材料の長さを\(L[m]\)、面積を\(S[m^2]\)とすると、
\(\displaystyle R=ρ\frac{L}{S}\)
高速道路の渋滞している道が長くなればなるほど、車の流れが詰まるのと同様に、電流が通りづらい経路が長ければ長いほど電流が流れなくなります。
\(L\)の大きさに比例して抵抗が増えることが感覚的にわかるとおもいます。
高速道路の車線が1車線よりも2車線の方がスムーズに走れるのと同様に、電流が通りづらい抵抗材料の中でも、その電流経路の幅が広くなれば、通りやすくなります。
そのため、断面積\(S[m^2]\)が広くなれば抵抗が下がる反比例の関係も感覚的にわかると思います。
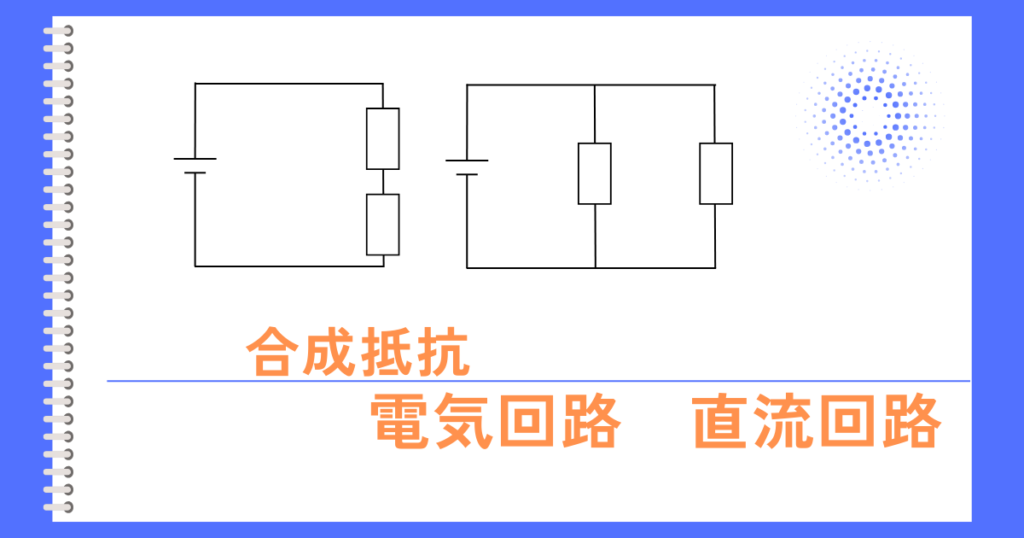
コンダクタンスG[S]
コンダクタンス\(G\)は、抵抗\(R\)の逆数で、電気の流れやすさを表します。
\(\displaystyle G=\frac{1}{R}\)
並列回路の計算をするときに、コンダクタンスを使うと計算を簡素化することが出来ます。
導電率σ[S/m]
導電率\(σ\)は、単位長さ当たりのコンダクタンス\(G\)です。
\(\displaystyle G=σ\frac{S}{L}\)
導電率\(σ\)は、抵抗率\(ρ\)の逆数で、電気の流れやすさを表します。
\(\displaystyle σ=\frac{1}{ρ}\)
抵抗温度係数[ppm/K]
導体において、物質は温度が上昇するほど抵抗率は大きくなり、低下するほど小さくなります。
温度と、抵抗値には一定の相関があります。
抵抗温度係数とは、抵抗の温度変化に伴う抵抗値の変化の割合を表す値です。
温度変化によって抵抗値が変化するのは、温度が上がると抵抗の原子の振動が激しくなることで、自由電子が抵抗の原子とぶつかる回数が多くなるため、抵抗値が増加します。
\(t_1[℃]\)の時の抵抗値を\(R_{t1}\)、\(t_2[℃]\)の時の抵抗値を\(R_{t2}\)、抵抗温度係数を\(α\)としたとき、
\(R_{t2}=R_{t1}(1+α(t_2-t_1))\)
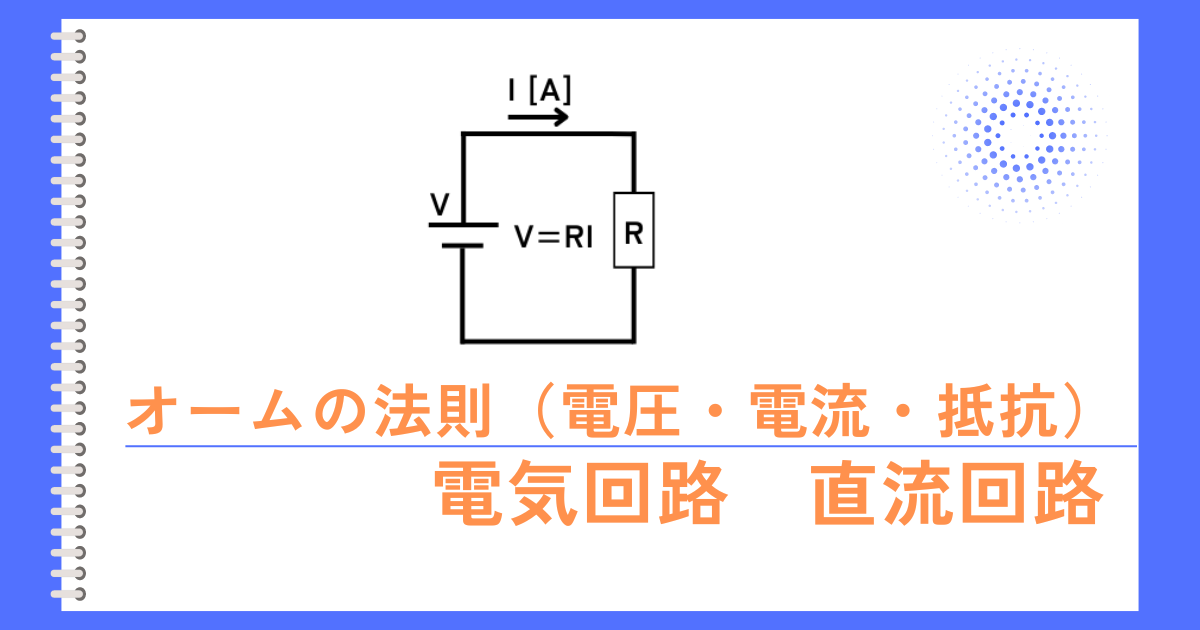
オームの法則
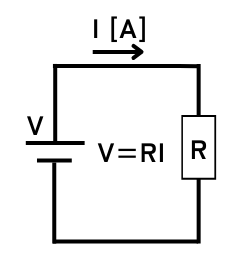
オームの法則は、電気回路における電圧\(V\)、電流\(I\)、抵抗\(R\)の関係性を示す法則で、「電圧は電流に比例する」ということを意味します。
オームの法則の式は、\(V=RI\)です。
消費電力
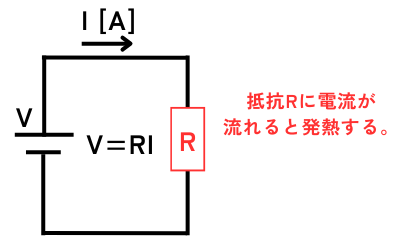
抵抗\(R[Ω]\)に電圧\(V[V]\)を印加して、電流\(I[A]\)が流れた時の消費電力を\(P[W]\)とします。このとき、
\(\displaystyle P=IV=I^2R=\frac{V^2}{R}[W]\)
が全て熱に変換されます。
消費電力は1秒当たりのジュール熱です。式で表すと、
\(\displaystyle P=\frac{J}{t}[W]\) ⇔ \(J=Pt[J]\)
消費電力\(P=VI\)となる理由
電圧\(V[V]\)は、単位電荷(\(1C\))が持つエネルギーです。 (参考解説ページ)
したがって、\(q[C]\)の時のエネルギーを\(W[J]\)とすると、
\(W=qV\) ⇔ \(\displaystyle V=\frac{W}{q}\) …①
電流\(I[A]\)は、単位時間(1秒間)に何Cの電荷が流れたかを表す物理量です。
したがって、\(\displaystyle I=\frac{q}{t}\) …②
\(VI\)は、①×②式なので、
\(\displaystyle V・I=\frac{W}{q}・\frac{q}{t}=\frac{W}{t}\) …③
消費電力\(P[W]\)は、単位時間(1秒間)に消費されるエネルギー\(W\)を表します。
したがって、\(\displaystyle P=\frac{W}{t} \) …④
③・④式から、\(P=VI\)であることが導出できました。
消費電力の最大値
電験の問題では、内部抵抗\(r[Ω]\)のある電圧\(V[V]\)の電池を可変抵抗\(R[Ω]\)に接続したときに、可変抵抗\(R[Ω]\)の消費電力が最大となるときの抵抗値を求める問題が時々出題されます。
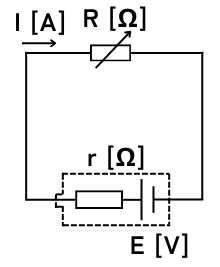
内部抵抗\(r\)、可変抵抗\(R\)としたとき、消費電力は最大となる可変抵抗値\(R\)は、\(R=r[Ω]\)のときです
\(R=r[Ω]\)のときに消費電力が最大となる理由の導出
回路に流れる電流\(I[A]\)は、
\(\displaystyle I=\frac{E}{r+R}\) …①
可変抵抗\(R\)の消費電力\(P[W]\)は、
\(\displaystyle P=I^2R=\left( \frac{E}{r+R} \right)^2 R=\frac{E^2R}{(r+R)^2}\) …②
消費電力\(P\)の最大値を求めるには、消費電力\(P\)を可変抵抗\(R\)で微分した時の値が\(0\)となるときに最大となります。これを式で表すと、次式となります。
\(\displaystyle \frac{dP}{dR}=0\) …③
③式に②式を代入して微分をすると、
\(\displaystyle \frac{dP}{dR}=\frac{(r+R)^2E^2-E^2R・2(r+R)}{((r+R)^2)^2}=\frac{(r-R)E}{(r+R)^3}=0\)
したがって、\(R=r\)のとき、\(\frac{dP}{dR}=0\)となります。
分数の微分
\(\frac{dP}{dR}=0\) を求めるときに、分数の微分を使いました。
分数の微分の公式は、次式で表されます。
\(\displaystyle \left( \frac{f(x)}{g(x)}\right)’=\frac{f’(x)g(x)-f(x)g’(x)}{( g(x))^2}\)
過去問
難易度 ★☆☆☆☆
| 電験三種 令和5年度上期 問7 | 抵抗の温度係数による電流の変化 |
関連記事(直流回路に関する解説)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント