磁気回路とは
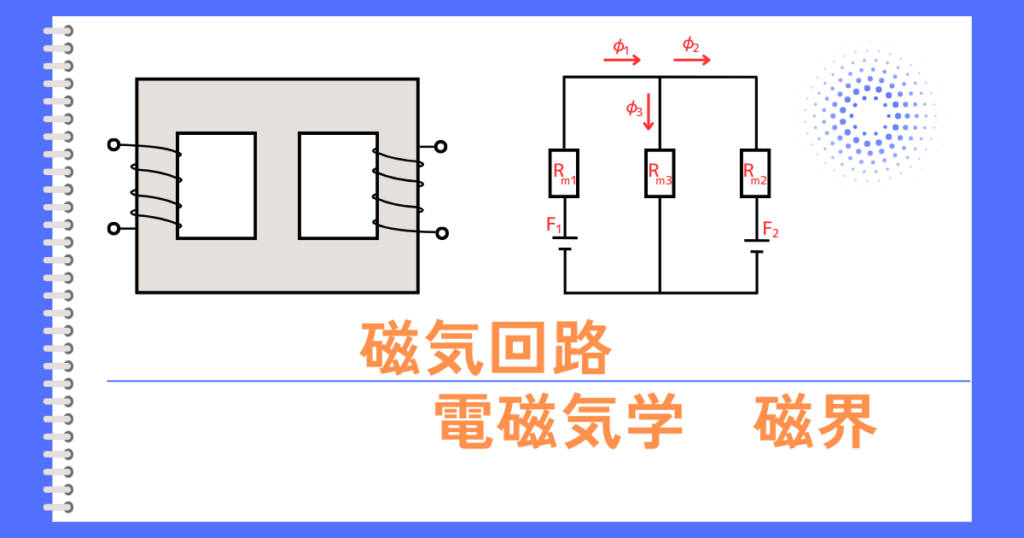
鉄心にコイルを巻いて電流を流すと発生する磁束は、鉄心の中を通ります。
環状鉄心のようにループする経路がある場合、磁束が電流のようにループします。
電気回路における各種の法則が鉄心内を流れる磁束においても成り立つので、磁気回路と呼びます。
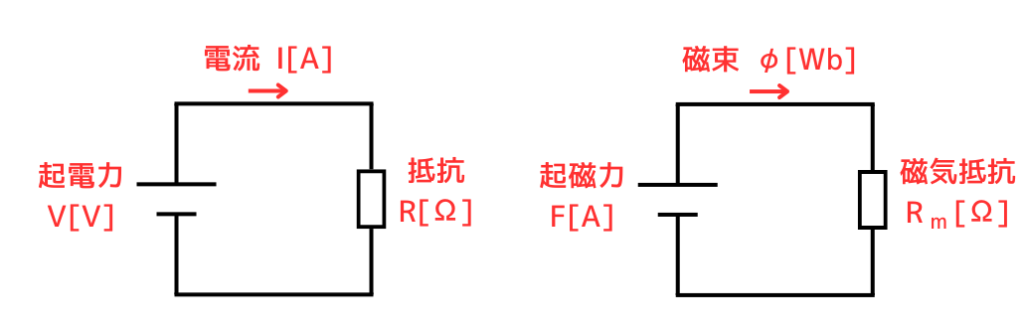
電気回路における「起電力」「電流」「抵抗」は、磁気回路では「起磁力」「磁束」「磁気抵抗」と置き換わります。
公式一覧
磁気回路に関する公式をまとめました。
起磁力
\(F=NI=Hl[A]\)
磁束
\(\Phi =BS[Wb]\)
磁気抵抗
\(\displaystyle R_m=\frac{l}{μS}[H^{-1}]\)
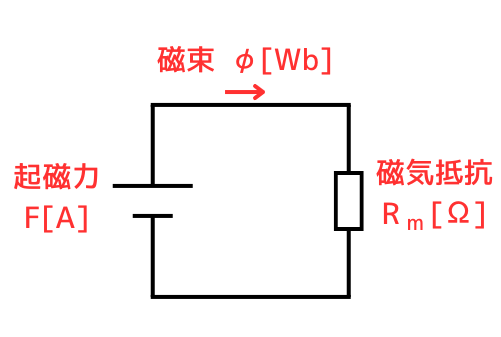
磁気回路のオームの法則
\(F=\Phi R_m\)
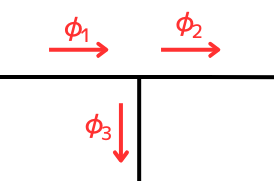
磁気回路のキルヒホッフの法則
分岐点に流入する磁束 = 分岐点から流出する磁束
\(\Phi_1=\Phi_2+\Phi_3\)
磁気回路で成り立つ法則
磁気回路で成り立つ法則
・オームの法則 \(F=\Phi R_m\)
・キルヒホッフの法則 \(\Phi_1=\Phi_2+\Phi_3\)
・重ねの理
等の、電気回路で成り立つ法則・定理は磁気回路でも成り立ちます。
オームの法則 \(F=\Phi R_m\)
電気回路のオームの法則\(V=IR\)と同様に、磁気回路でもオームの法則\(F=\Phi R_m\)が成り立ちます。
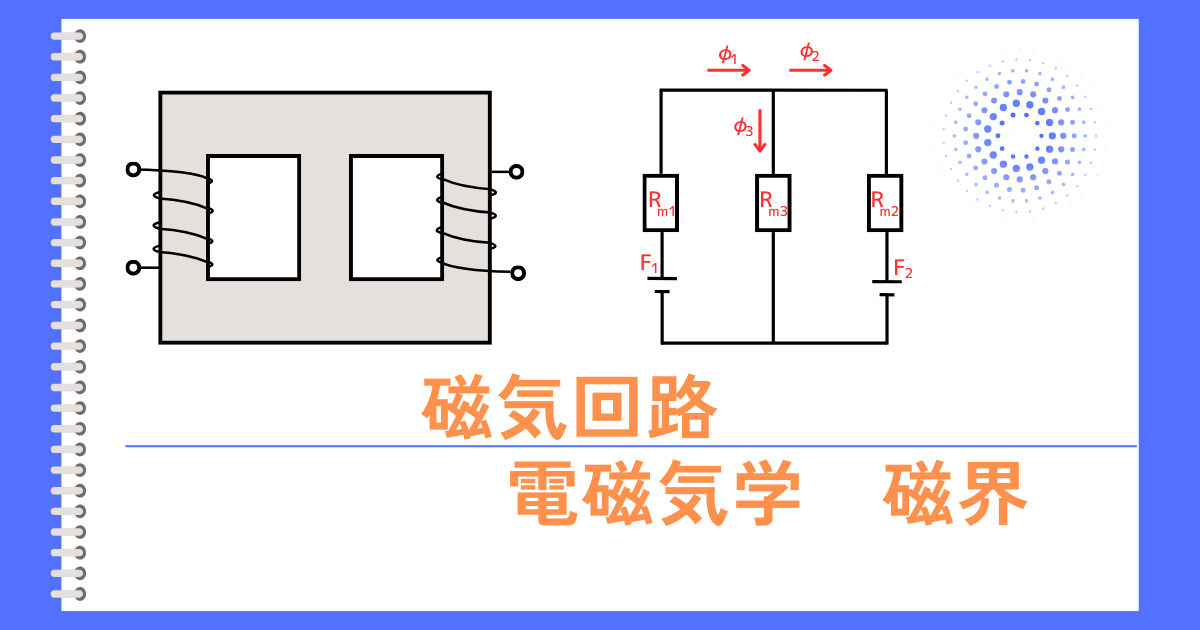
キルヒホッフの法則 \(\Phi_1=\Phi_2 +\Phi_3\)
磁気回路における磁束\(\Phi[Wb]\)は、電気回路における電流\(I[A]\)と同様にキルヒホッフの法則(電流則)が成り立ちます。
キルヒホッフの電流則は、電気回路の分岐点や合流点において、流入する電流の総和と流出する電流の総和が等しいという法則です。
磁気回路の場合は、流入する磁束の総和と流出する磁束の総和が等しくなります。
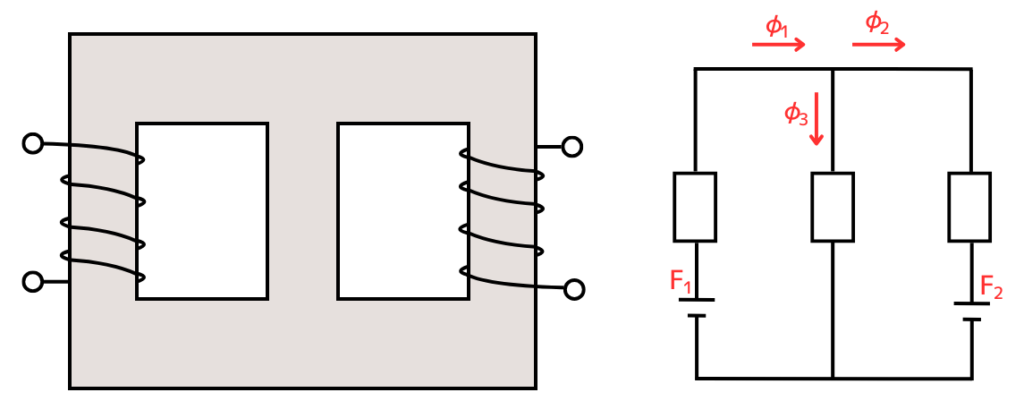
重ねの理
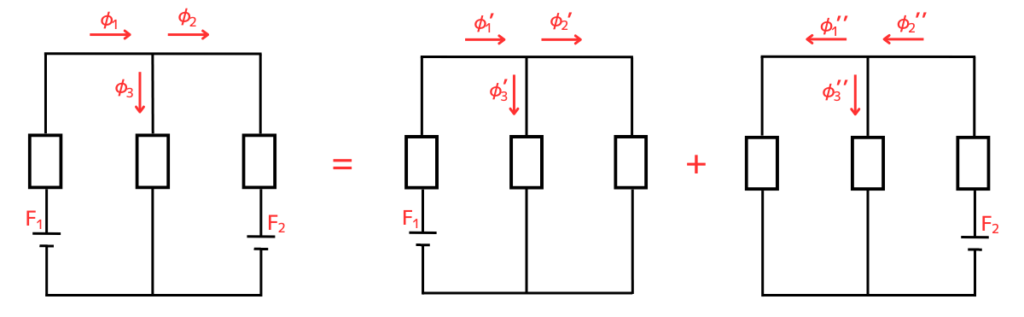
磁気回路に2つの起磁力\(F_1\)、\(F_2\)があるとき、\(F_1\)が作る磁束と、\(F_2\)が作る磁束の和を取ることで、磁気回路全体の磁束が求められます。
\(\Phi_1=\Phi_1 ’+\Phi_1 ’’\)
\(\Phi_2=\Phi_2 ’+\Phi_2 ’’\)
\(\Phi_3=\Phi_3 ’+\Phi_3 ’’\)
磁気回路の基本
起磁力
起磁力\(F\)とは、磁気回路に磁束を生じさせる力です。電気回路における電圧\(V\)と対応しています。
起磁力の式:\(F=NI=Hl[A]\)
起磁力の関係式(\(F=NI\))のイメージ
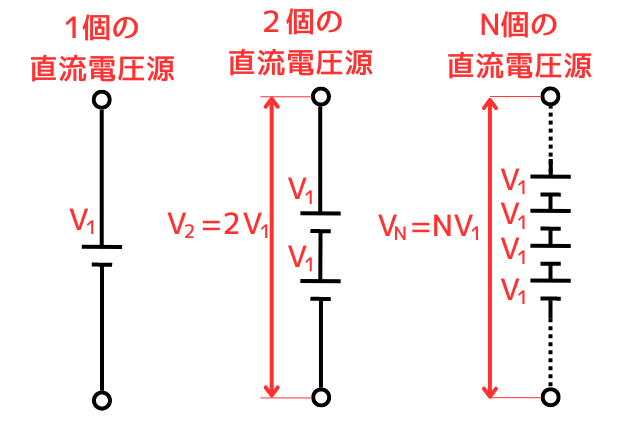
\(N\)回巻のコイルに電流\(I[A]\)が流れている時の起磁力\(F\)の関係式\(F=NI\)は、一個\(V_1[V]\)の直流電圧源を\(N\)個直列接続した時(\(V_N=NV_1\))と同じイメージです。
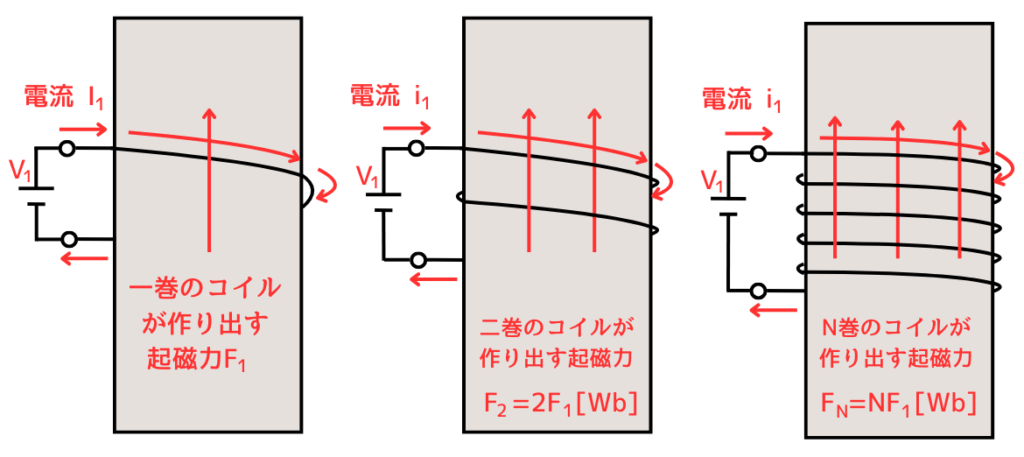
一回巻のコイルの起磁力を\(F_1\)としたとき、\(F_1=I\)
二回巻のコイルの起磁力を\(F_2\)としたとき、\(F_2=2F_1=2I\)
\(N\)回巻のコイルの起磁力を\(F\)としたとき、\(F_N=NF_1=NI\)
1個の直流電圧源の電圧を\(V_1\)としたとき、
2個の直流電圧源を直列接続した時の電圧は\(V_2=2V_1\)
\(N\)個の直流電圧源を直列接続した時の電圧は\(V_N=NV_1\)
起磁力の関係式(\(F=Hl\))
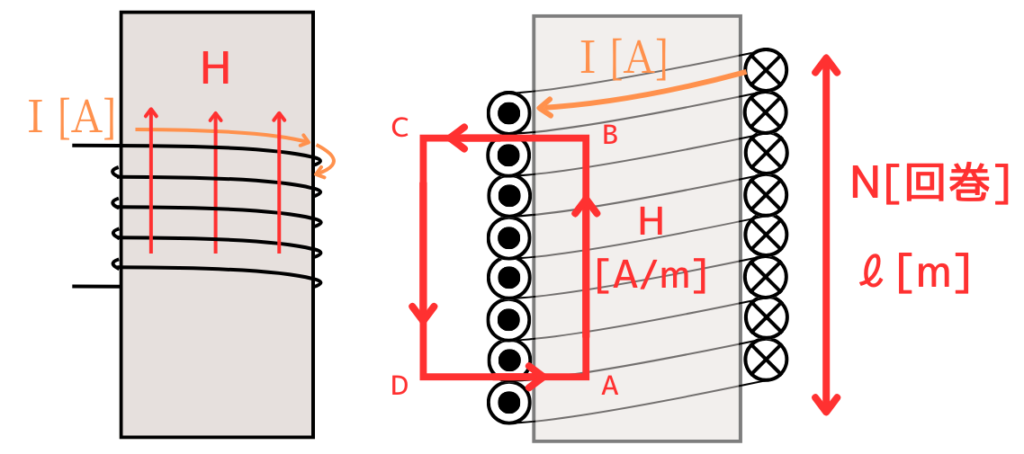
磁気回路の起磁力を生み出すコイル部分は、無限長ソレノイドとして扱います。
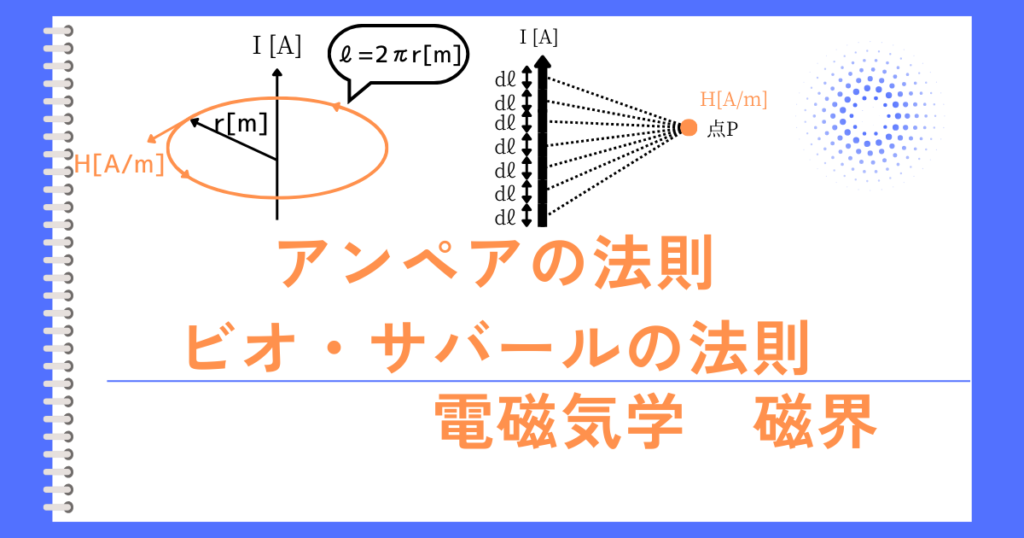
コイルの巻数\(N\)[回巻]、コイルに流れる電流\(I[A]\)、磁界の強さ\(H[A/m]\)、磁気回路の長さ(磁路長)\(l[m]\)としたとき、アンペールの法則から、
\(\begin{eqnarray}
\oint Hdl&=&\int_A^B H dl+\int_B^C H dl+\int_C^D H dl+\int_D^A H dl\\
&=&Hl+0+0+0\\
&=&Hl
\end{eqnarray}\)
以上より、起磁力の関係式は、\(F=Hl\)です。
起磁力まとめ
\(F=NI\)、\(F=Hl\)の上記2つの式は、どちらも磁気回路の問題で頻繁に使用します。
そのため、\(F=NI=Hl\)として覚えると良いでしょう。
磁束
磁束は、鉄心を通過する磁気の量です。電気回路における電流\(I\)と対応しています。
磁束の式:\(\Phi =BS[Wb]\)
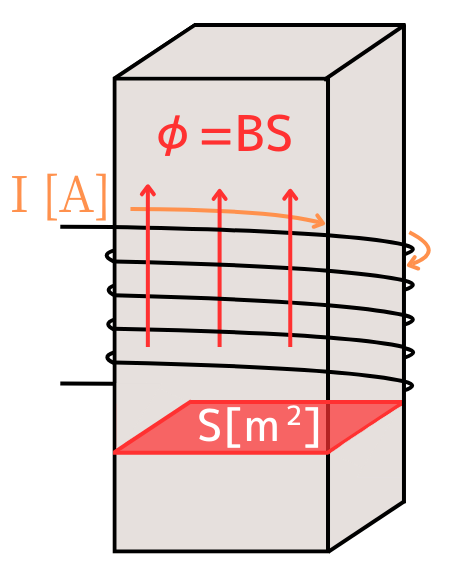
磁束\(\Phi\)の式
磁束密度\(B[T]\)は、磁束\(\Phi [Wb]\)の密度なので、磁路の面積\(S[m^2]\)を使って表すと、
\(\Phi =BS[Wb]\)
です。
余談(覚える必要はないです)
磁気回路の問題では、透磁率\(μ[H/m]\)、コイルの巻数\(N\)[回]、コイルに流れる電流\(I[A]\)、磁路長\(l[m]\)の条件を与えられることは多いですが、磁束密度\(B\)が与えられることは少ないです。
そのため、磁束\(\Phi\)を求める場合、ある程度式変形をする必要があります。
その式変形について示してみます。
磁束密度\(B[T]\)と、磁界強度\(H[A/m]\)、透磁率\(μ[H/m]\)の関係式は、\(B=μH\)
起磁力の式を変形すると、\(F=NI=Hl[A]\)⇔\(\displaystyle H=\frac{NI}{l}\)
これを磁束\(\Phi\)の式に代入すると、
\(\displaystyle \Phi=BS=μHS=\frac{μNIS}{l}\)となります。
式変形をすれば簡単に導き出せる式なので、\(\displaystyle \Phi=\frac{μNIS}{l}\)の式は、覚える必要性は無いです。
磁気抵抗
磁気回路における磁束の流れにくさを表す度合いです。電気回路における抵抗\(R\)と対応しています。
磁気抵抗:\(\displaystyle R_m=\frac{l}{μS}[H^{-1}]\)
磁気抵抗の関係式の導出
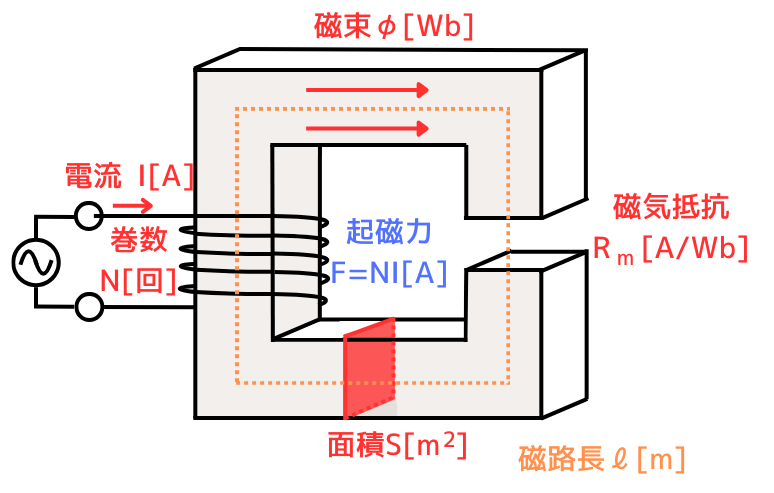
磁気回路のオームの法則から
\(F=\Phi R_m\) ⇔ \(\displaystyle R_m=\frac{F}{\Phi}\) …①
起磁力\(F\)の式 \(F=NI=Hl\) …②
磁束\(\Phi\)の式 \(\Phi=BS\) …③
磁束密度\(B\)と磁界強度\(H\)の関係式 \(B=μH\) …④
起磁力の式②から磁界強度\(H\)について変形した式 \(\displaystyle H=\frac{NI}{l}\) …⑤
①式に②~⑤式を代入していく
\(\displaystyle R_m=\frac{F}{\Phi}=\frac{NI}{BS}=\frac{NI}{μHS}=\frac{NI}{μ\frac{NI}{l}S}=\frac{l}{μS}\)
以上より、\(\displaystyle R_m=\frac{l}{μS}[H^{-1}]\)が導出できました。
磁気抵抗(\(\displaystyle R_m=\frac{l}{μS}\))の式の感覚的な覚え方
①磁気回路の面積\(S\)が広くなれば、磁束\(\Phi \)が通る道は広くなります。
⇒磁束が流れやすくなり、磁気抵抗\(R_m\)は小さくなる。
②磁路長\(l[m]\)が長くなると、磁束が流れる抵抗が長くなります。
⇒磁気抵抗\(R_m\)は長くなった分、大きくなります。
③透磁率\(μ\)は、磁束がどれくらい通しやすいかを表します。
透磁率\(μ\)が大きくなると、磁束が通りやすくなります。
⇒磁気抵抗\(R_m\)は小さくなります。
電気回路と磁気回路の比較
| 電気回路 - 磁気回路対応表 | |
|---|---|
| 電気回路 | 磁気回路 |
| 起電力 \(V[V]\) | 起磁力 \(F[A]\) |
| 電流 \(I[A]\) | 磁束 \(\Phi [Wb]\) |
| 抵抗(レジスタンス) \(\displaystyle R=ρ\frac{l}{S}=\frac{l}{σS}[Ω]\) \(ρ\):抵抗率[Ωm]、\(σ\):導電率[S/m] | 磁気抵抗(リラクタンス) \(\displaystyle R_m=\frac{l}{μS}[H^{-1}]\) |
| オームの法則 \(V=IR\) | オームの法則 \(F=\Phi R_m\) |
| 導電率 \(σ[S/m]\) | 透磁率 \(μ[H/m]\) |
過去問
難易度 ★☆☆☆☆
| 電験三種 令和5年度上期 問3 | 磁気抵抗に関する論説 |
難易度 ★★☆☆☆
| 電験三種 令和5年度上期 問4 | 磁界に関する論説 |
| 電験三種 令和元年度上期 問4 | 環状ソレノイドの透磁率の計算 |
難易度 ★★★★☆
| 電験三種 令和4年度上期 問3 | 環状鉄心の結合係数の計算 |
関連記事(磁界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
コメント