キルヒホッフの法則とは
キルヒホッフの法則は、電気回路内の各部に流れる電流や、印加される電圧を解析をするために重要な法則です。キルヒホッフの法則は次の2つの法則から成り立ちます。
キルヒホッフの電流則
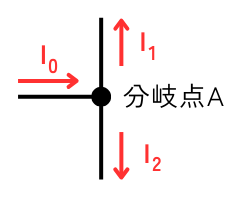
電気回路の分岐点に入ってくる電流の和=出て行く電流の和
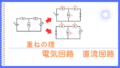
左図の分岐点Aの場合、\(I_0=I_1+I_2\)
キルヒホッフの電圧則
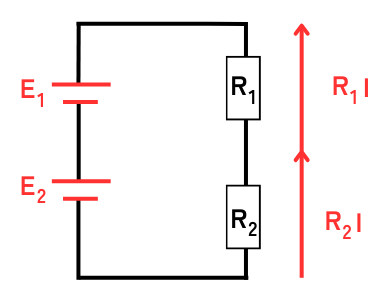
閉回路内の起電力の和=電圧降下の和
左図の閉回路の場合、\(E_1+E_2=R_1I+R_2I\)
キルヒホッフの法則を使った回路解析の例
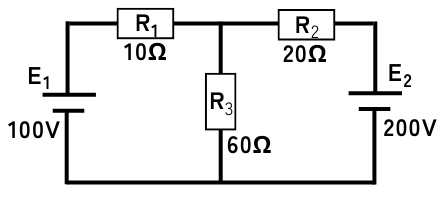
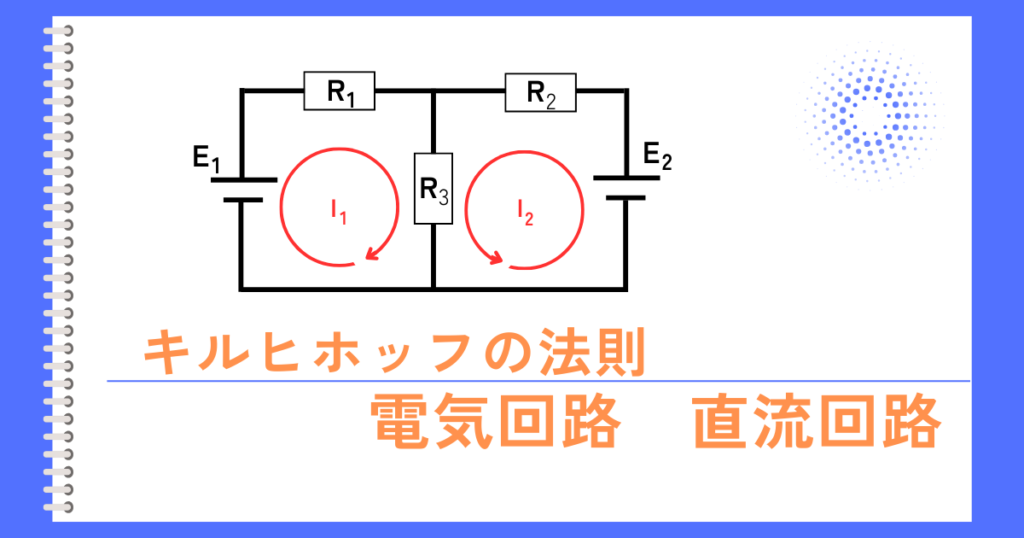
言葉で説明するよりも、実際に例題を解く方がわかりやすいと思うので、下図のような回路の例を用いて説明します。
2つの電圧源を使用した回路に、キルヒホッフの法則を使って各部の電圧・電流を解析します。
回路解析の手順は次の3ステップです。
1.電流\(I_1\)、\(I_2\)、\(I_3\)の流れる方向を決める
2.キルヒホッフの法則から、連立方程式を立式する
3.連立方程式を解く
1.電流\(I_1\)、\(I_2\)、\(I_3\)の流れる方向を決める
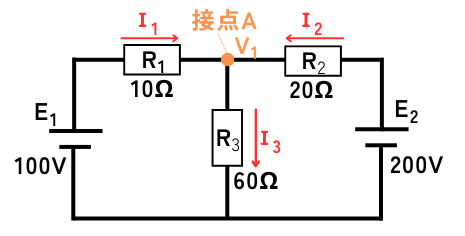
・抵抗\(R_1\)に流れる電流\(I_1\)の向きは左から右を正とする。
・抵抗\(R_2\)に流れる電流\(I_2\)の向きは右から左を正とする。
・抵抗\(R_3\)に流れる電流\(I_3\)の向きは上から下を正とする。
2.キルヒホッフの法則から、連立方程式を立式する
キルヒホッフの電流則から、接点Aに流入・流出する電流は、
\(I_1+I_2=I_3\) …①
接点Aの電圧を\(V_1\)とすると、オームの法則から次の3式が成り立ちます。
\(V_1=I_3R_3\) …②
\(I_1=\frac{E_1-V_1}{R_1}=\frac{E_1-I_3R_3}{R_1}\)
⇔\(I_1R_1=E_1-I_3R_3\) …③
\(I_2=\frac{E_2-V_1}{R_2}=\frac{E_2-I_3R_3}{R_2}\)
⇔\(I_2R_2=E_2-I_3R_3\) …④
①~④式に各抵抗値を代入して整理すると
\(\begin{eqnarray} \left\{
\begin{array}{l}
I_1+I_2=I_3 …①\\
V_1=60I_3 …⑤\\
10I_1=100-60I_3 ⇔ I_1=10-6I_3 …⑥\\
20I_2=200-60I_3 ⇔ I_2=10-3I_3 …⑦
\end{array}
\right.
\end{eqnarray}\)
3.連立方程式を解く
⑥式ー⑦式×2 を計算すると、
\(I_1-2I_2=-10\) ⇔ \(I_1=2I_2-10\) …⑧
⑧式を①式に代入すると、
\(3I_2-10=I_3\) ⇔ \(3I_2=10+I_3\) …⑨
⑦式+⑨式×3 を計算すると、
\(10I_2=40\) ⇔ \(I_2=4\) …⑩
⑩式を⑨式に代入すると、\(I_3=2\) …⑪
⑩・⑪式を①式に代入すると、\(I_1=-2\)
⑪式を⑤式に代入すると、\(V_1=120\)
以上より、\(V_1=120\)、\(I_1=-2\)、\(I_2=4\)、\(I_3=2\)であることがわかりました。
なお、\(I_1\)は負の値なので、右から左に2A流れています。
実用的な連立方程式
接点毎に、電流則を使って立式していくのは大変なので、より簡単に連立方程式を立てられる方法を説明します。
回路解析の手順は次の3ステップです。
1.小さな閉回路を循環する電流\(I_1\)、\(I_2\)を書く。
2.キルヒホッフの電圧則に従って連立方程式を立式する。
3.連立方程式を解く。

1.小さな閉回路を循環する電流\(I_1\)、\(I_2\)を書く。
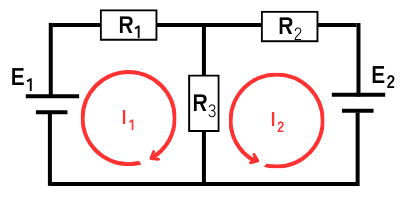
左図のように、2つの最小の閉回路に二つの電流を描きます。
\(I_1\)は、\(E_1\)から出力されて循環する時計回りを正とした電流。
\(I_2\)は、\(E_2\)から出力されて循環する反時計回りを正とした電流。
※ここで定める電流の向きは、時計回りでも、反時計回りでも構いません。
2.キルヒホッフの電圧則に従って連立方程式を立式する。
\(\begin{eqnarray} \left\{
\begin{array}{l}
E_1=R_1I_1+R_3(I_1+I_2)\\
E_2=R_2I_2+R_3(I_1+I_2)
\end{array}
\right.
\end{eqnarray}\)
電源電圧と、抵抗値を代入すると、
\(\begin{eqnarray} \left\{
\begin{array}{l}
100=10I_1+60(I_1+I_2)\\
200=20I_2+60(I_1+I_2)
\end{array}
\right.
\end{eqnarray}\)
3.連立方程式を解く。
連立方程式を整理すると、①・②式となります。
\(\begin{eqnarray} \left\{
\begin{array}{l}
100=70I_1+60I_2 …①\\
200=60I_1+80I_2 …②\\
\end{array}
\right.
\end{eqnarray}\)
①式×4ー②式×3を計算すると、
\(-200=100I_1\) ⇔ \(I_1=-2\) …③
③式を①式に代入して整理すると、\(I_2=4\)
以上より、\(I_1\)は反時計回りに\(2A\)、\(I_2\)は反時計回りに\(4A\)流れていることがわかりました。このことから、各抵抗に流れる電流、接点の電圧を求めます。
抵抗\(R_1\)に流れる電流は\(I_1\)なので、右から左に\(2A\)流れます。
抵抗\(R_2\)に流れる電流は\(I_2\)なので、右から左に\(4A\)流れます。
抵抗\(R_3\)に流れる電流は\(I_1+I_2\)なので、上から下に\(2A\)流れます。
接点の電圧は\(V=I_3R_3=120V\)です。
過去問
難易度 ★★☆☆☆
| 電験三種 令和5年度下期 問6 | 2電源回路の解析 |
| 電験三種 令和5年度上期 問5 | 2電源回路の解析 |
| 電験三種 令和5年度上期 問6 | 電圧源・電流源からなる2電源回路の解析 |
関連記事(直流回路に関する解説)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント