インダクタンスとは
コイルに流れる電流が変化した時に生じる起電力と、電流の変化率をつなげる比例定数をインダクタンスと呼びます。
インダクタンスは、自己インダクタンスと、相互インダクタンスに大別されます。
単にインダクタンスと呼ぶ際は、自己インダクタンスを指すことが多いです。
公式一覧
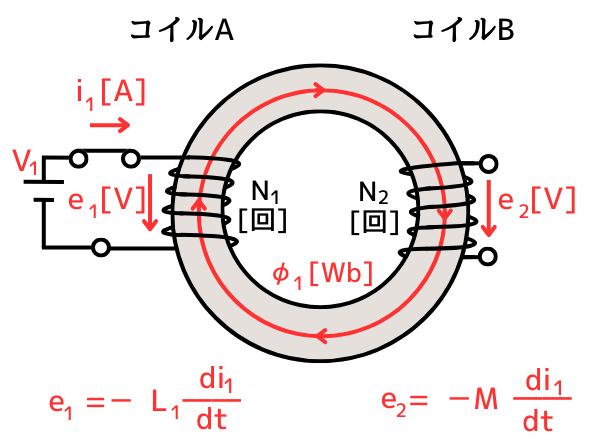
自己インダクタンス\(L[H]\)と誘導起電力\(e[V]\)
\(\displaystyle e_1=-L_1\frac{di_1}{dt}=-N_1\frac{d\Phi_1}{dt}\)
相互インダクタンス\(M[H]\)と誘導起電力\(e[V]\)
\(\displaystyle e_2=-M\frac{di_1}{dt}=-N_2\frac{d\Phi_1}{dt}\)
結合係数\(k\)
\(\displaystyle k=\frac{M}{\sqrt{L_1L_2}}\)
数字の範囲は、\(k=0~1\)です。
ファラデーの電磁誘導の法則による誘導起電力
\(\displaystyle e=-N\frac{d\Phi}{dt}\)
和動接続の時の合成インダクタンス\(L[H]\)
合成された自己インダクタンス\(L\)は、コイルAの自己インダクタンスを\(L_1\)、コイルBの自己インダクタンスを\(L_2\)、相互インダクタンスを\(M\)とするとき、次式で表されます。
\(L=L_1+L_2+2M\)
差動接続の時の合成インダクタンス\(L[H]\)
合成された自己インダクタンス\(L\)は、コイルAの自己インダクタンスを\(L_1\)、コイルBの自己インダクタンスを\(L_2\)、相互インダクタンスを\(M\)とするとき、次式で表されます。
\(L=L_1+L_2-2M\)
インダクタンス
自己インダクタンス L
自己インダクタンス\(L[H]\)と誘導起電力\(e[V]\)
自己インダクタンス\(L\)と誘導起電力の関係は、次式で表すことができます。
\(\displaystyle e=-L\frac{di}{dt}\)
コイルに流れる電流が変化すると、電流の変化が磁束の変化となります。
コイルの中を通過する磁束の量が変化すると、ファラデーの電磁誘導の法則にしたがい、磁束の変化を妨げる向きに逆起電力が生じます。
この作用を自己誘導作用と呼び、生じた逆起電力は誘導起電力と呼びます。
自己誘導作用によって生じる誘導起電力\(e[V]\)は、電流の時間変化の割合\(\frac{di}{dt}\)に比例します。
この\(e\)と\(\frac{di}{dt}\)を結びつける比例定数\(L\)を、自己インダクタンスと呼びます。
自己誘導作用による誘導起電力が発生するまでの経緯
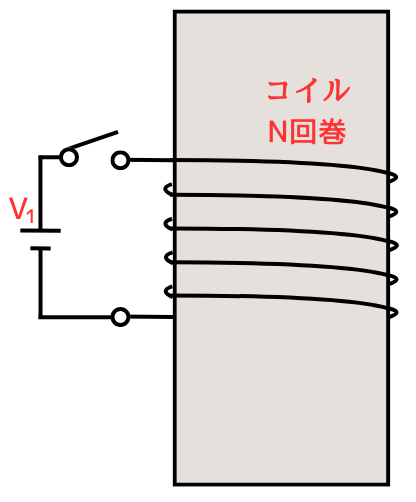
N巻のコイルに、スイッチを挟んで直流電圧源\(V_1\)を接続します。
初めは、スイッチを開放した状態としておきます。
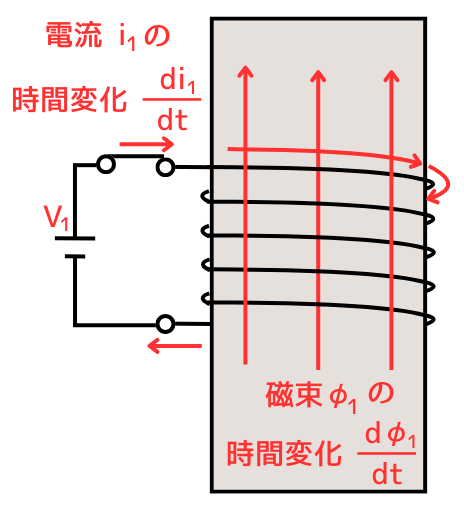
あるタイミングでスイッチをONしたとします。
このとき、コイルに流れ始める電流\(i_1[A]\)の時間変化は\(\frac{di_1}{dt}\)です。
コイルに流れる電流\(i_1[A]\)によって発生した磁束は鉄心を流れます。鉄心に流れる磁束\(\Phi_1[Wb]\)の時間変化は\(\frac{d\Phi_1}{dt}\)です。
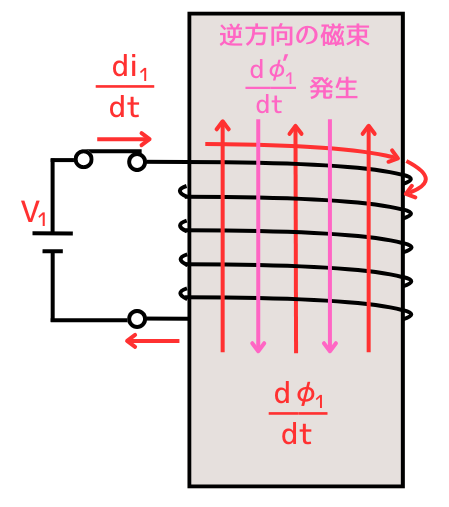
コイルを貫く磁束が\(\frac{d\Phi_1}{dt}\)だけ時間変化するので、磁束の変化を妨げる方向に、\(\frac{d\Phi_1’}{dt}\)の磁束が発生します。
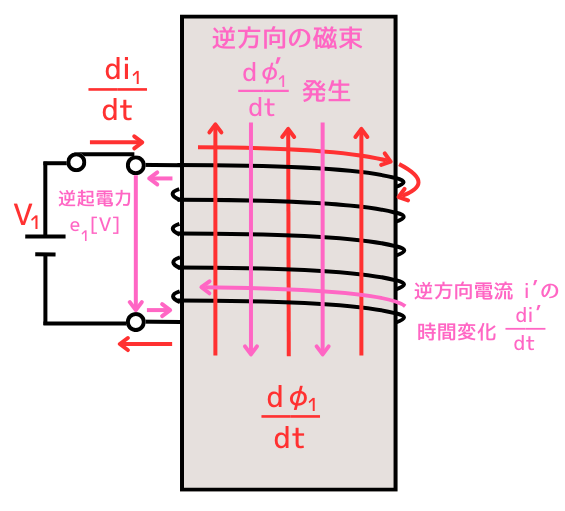
磁束の変化を妨げる磁束\(\frac{d\Phi_1’}{dt}\)によって、逆方向電流\(i’[A]\)が流れます。
この逆方向電流\(i’[A]\)を流すために、誘導起電力(逆方向起電圧)\(e_1[V]\)が発生します。
補足(過渡現象)
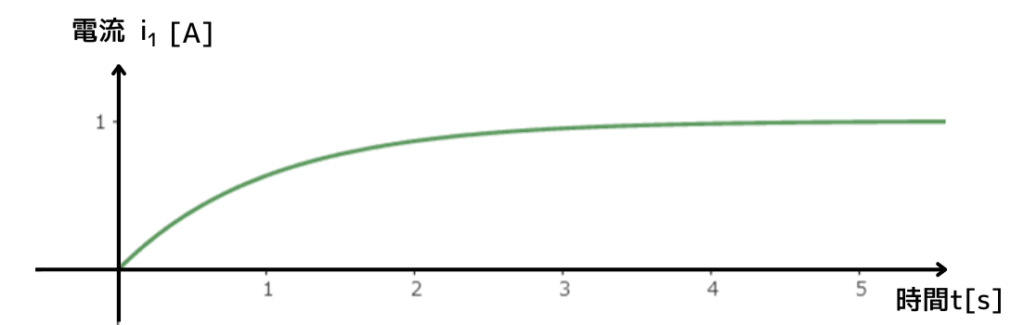
電流\(i_1\)と、逆方向電流\(i’\)を合成した電流(\(i=i_1-i’\))が、コイルに実際に流れる電流です。
スイッチをつなげた直後\(t=0[s]\)の瞬間は、\(i_1=i’\)となるので、瞬間的にコイルに流れる電流は\(0[A]\)となります。
時間の経過に伴って、\(\frac{di_1}{dt}\)が減少することによって\(i’\)が減少します。
その結果、コイルに流れる電流\(i\) が増加します。
このような現象を過渡現象と呼び、直流回路の理論で重要な現象です。
相互インダクタンス M
相互インダクタンス\(M\)と誘導起電力\(e[V]\)
相互インダクタンス\(M[H]\)と誘導起電力の関係は、次式で表すことができます。
\(\displaystyle e_2=-M\frac{di_1}{dt}\)

鉄心に2つのコイルA・Bが巻かれており、片方のコイルAに流れる電流が変化したとき、もう片方のコイルBにも起電力を誘起します。
この作用を相互誘導作用と呼び、相互誘導作用によって生じる誘導起電力\(e[V]\)も、コイルAの電流の時間変化の割合\(\frac{di}{dt}\)に比例します。
この\(e\)と\(\frac{di}{dt}\)を結びつける比例定数\(M\)を、相互インダクタンスと呼びます。
結合係数 k
結合係数\(k\)は、次の式で示されます。
\(\displaystyle k=\frac{M}{\sqrt{L_1L_2}}\)
数字の範囲は、\(k=0~1\)です。
結合係数\(k\)は、鉄心に巻かれた2つのコイル間の結合度合いを示す係数です。
\(k\)が小さいと、鉄心を通らずに周囲に漏れ出てしまう漏れ磁束が多くなります。
漏れ磁束が多くなると、他方のコイルを貫く割合は小さくなりますので、片方のコイルに電流を流しても、他方に発生する誘導起電力は小さくなります。
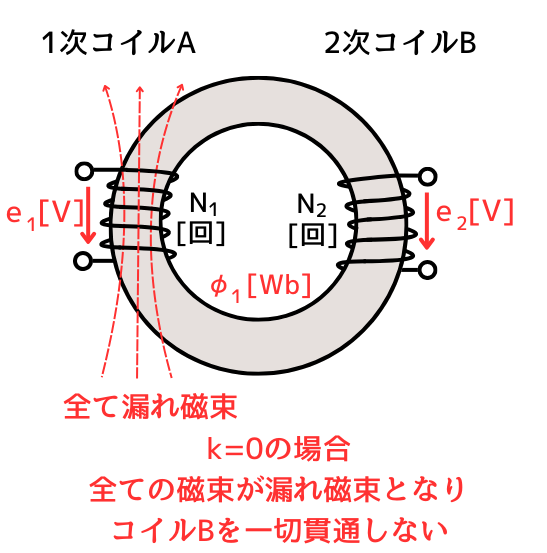
\(k=0\)の場合、片方のコイルが作った磁束は、全て漏れ磁束となるため、他方のコイルを一切貫きません。
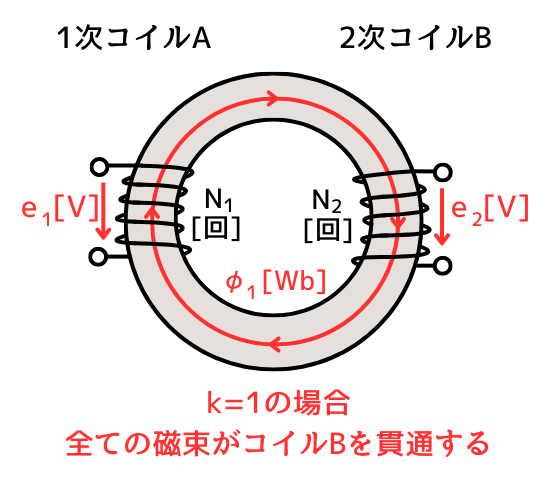
\(k=1\)の場合、片方のコイルが作った磁束は、全て他方のコイルを貫きます。
結合係数\(k\)の式の導出
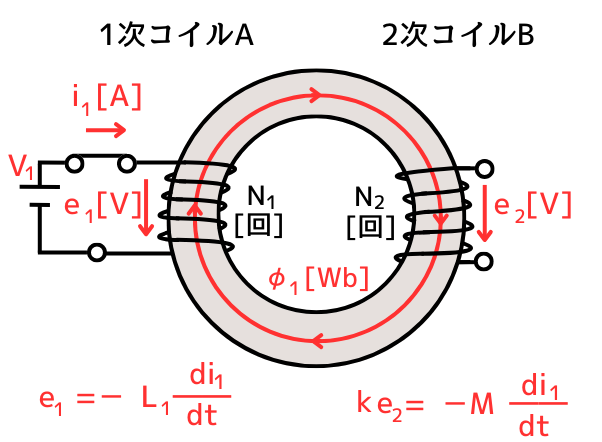
まず初めに、一次回路に電流変化を与えたときの自己誘導および相互誘導の関係式を示します。
\(\displaystyle \begin{eqnarray}
\left\{
\begin{array}{l}
e_1=-L_1 \frac{di_1}{dt} ………①\\
ke_2=-M \frac{di_1}{dt} ………②
\end{array} \right.
\end{eqnarray}\)
※②式は、結合係数によって誘導起電力\(e_2\)が変化するので、\(ke_2\)として表しています。
②÷①をすると、
\(\displaystyle k\frac{e_2}{e_1}=\frac{M}{L_1}\) ⇔ \(\displaystyle \frac{e_2}{e_1}=\frac{M}{kL_1}\) ………③
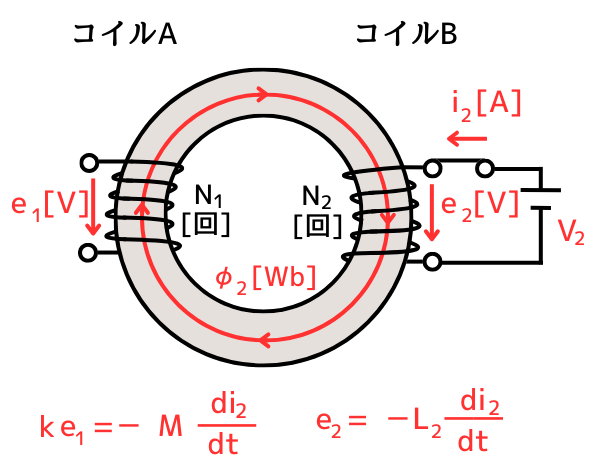
次に、二次回路に電流変化を与えたときの自己誘導および相互誘導の関係式を示します。
\(\displaystyle \begin{eqnarray}
\left\{\begin{array}{l}
ke_1=-M \frac{di_2}{dt} ………④\\
e_2=-L_2 \frac{di_2}{dt} ………⑤
\end{array} \right.
\end{eqnarray}\)
※④式は、結合係数によって誘導起電力\(e_1\)が変化するので、\(ke_1\)として表しています。
④÷⑤をすると、
\(\displaystyle k\frac{e_1}{e_2}=\frac{M}{L_2}\)
⇔\(\displaystyle \frac{e_1}{e_2}=\frac{M}{kL_2}\) ………⑥
最後に、③・⑥式から、結合係数kについて整理します。
\(\displaystyle \frac{M}{kL_1}=\frac{kL_2}{M}\)
⇔\(M^2=k^2L_1L_2\)
⇔\(M=k\sqrt{L_1L_2}\)
⇔\(\displaystyle k=\frac{M}{\sqrt{L_1L_2}}\)
鉄心に巻かれた複数のコイルの接続
1次コイルAと、2次コイルBを接続する方法には2つあります。
①和動接続:磁束が発生する方向を合わせて接続する方法
②差動接続:磁束が発生する方向が逆向きになるように接続する方法
和動接続
和動接続の時の合成インダクタンス\(L[H]\)
合成された自己インダクタンス\(L\)は、コイルAの自己インダクタンスを\(L_1\)、コイルBの自己インダクタンスを\(L_2\)、相互インダクタンスを\(M\)とするとき、次式で表されます。
\(L=L_1+L_2+2M\)
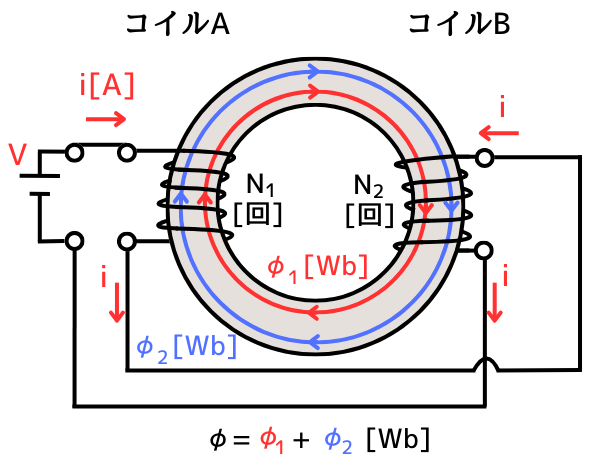
和動接続
左図のように、コイルAに電流を流した時に発生する磁束\(\phi_1\)の方向と、コイルBに電流を流した時に発生する磁束\(\phi_2\)の方向を合わせるように、コイルAとコイルBを接続した時を和動接続と呼びます。
この時の合成インダクタンス\(L\)を求めます。
\(Li=N_1(\phi_1+\phi_2)+N_2(\phi_1+\phi_2)\)
⇔\(Li=N_1\phi_1+N_1\phi_2+N_2\phi_1+N_2\phi_2\)
⇔\(Li=L_1i+Mi+Mi+L_2i\)
⇔\(L=L_1+L_2+2M\)
※式変形の途中で下記の関係式を使っています。
・\(L_1i=N_1\phi_1\)
・\(L_2i=N_2\phi_2\)
・\(Mi=N_1\phi_2=N_2\phi_1\)
差動接続
差動接続の時の合成インダクタンス\(L[H]\)
合成された自己インダクタンス\(L\)は、コイルAの自己インダクタンスを\(L_1\)、コイルBの自己インダクタンスを\(L_2\)、相互インダクタンスを\(M\)とするとき、次式で表されます。
\(L=L_1+L_2-2M\)
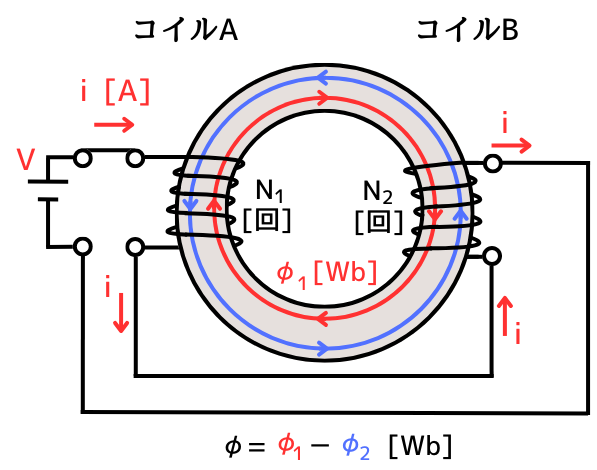
差動接続
左図のように、コイルAに電流を流した時に発生する磁束\(\phi_1\)の方向と、コイルBに電流を流した時に発生する磁束\(\phi_2\)の方向が逆を向くように、コイルAとコイルBを接続した時を差動接続と呼びます。
この時の合成インダクタンス\(L\)を求めます。
\(Li=N_1(\phi_1-\phi_2)+N_2(\phi_1-\phi_2)\)
⇔\(Li=N_1\phi_1-N_1\phi_2+N_2\phi_1-N_2\phi_2\)
⇔\(Li=L_1i-Mi+L_2i-Mi\)
⇔\(L=L_1+L_2-2M\)
磁束鎖交数
磁束鎖交数と磁束
磁束鎖交数と磁束
磁束鎖交数\(\Phi[Wb]\)とは、コイル全体を貫く磁束のことです。
コイルの巻数が\(N\)[回]、磁束を\(\phi[Wb]\)とした時、\(\phi[Wb]\)の磁束が、コイルの巻線を\(N\)回貫くことになるので、磁束鎖交数は次の式で表されます。
\(\Phi=N\phi [Wb]\)
磁束鎖交数は\(\Phi\) (大文字のファイ)
磁束は\(\phi\) (小文字のファイ)
の記号で表しますので、大文字の\(\Phi\)と、小文字の\(\phi\)に注意。
磁束と自己インダクタンス
誘導起電力\(e\)・磁束\(\phi\)・自己インダクタンス\(L\)の関係式
\(\displaystyle e=-N\frac{d\phi}{dt}=-L\frac{di}{dt}\)
磁束鎖交数\(\Phi\)・磁束\(\phi\)・自己インダクタンス\(L\)の関係式
\(\Phi=N\phi=LI\)
磁束\(\phi\)・自己インダクタンス\(L\)の関係式の導出
ファラデーの電磁誘導の法則から、
\(e=-\Phi=-N\frac{d\phi}{dt}\) …①
自己インダクタンス\(L\)と誘導起電力の関係から、
\(e=-L\frac{dI}{dt}\) …②
①・②式から
\(-N\frac{d\phi}{dt}=-L\frac{dI}{dt}\)
⇔\(N d\phi = L dI\)
磁束\(\phi\)と、電流\(I\)は比例するので、
⇔\(N\phi=LI\)
過去問
難易度 ★★☆☆☆
| 電験三種 令和3年度 問4 | 電磁誘導(磁束鎖交数・誘導起電力)の計算 |
難易度 ★★★★☆
| 電験三種 令和4年度上期 問3 | 環状鉄心の結合係数の計算 |
関連記事(磁界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント