【電験三種：理論】平成２１年度　問５

難易度

直流のコンデンサ回路に関する基礎知識問題です。
高校レベルなので、確実に回答したい問題です。

問題

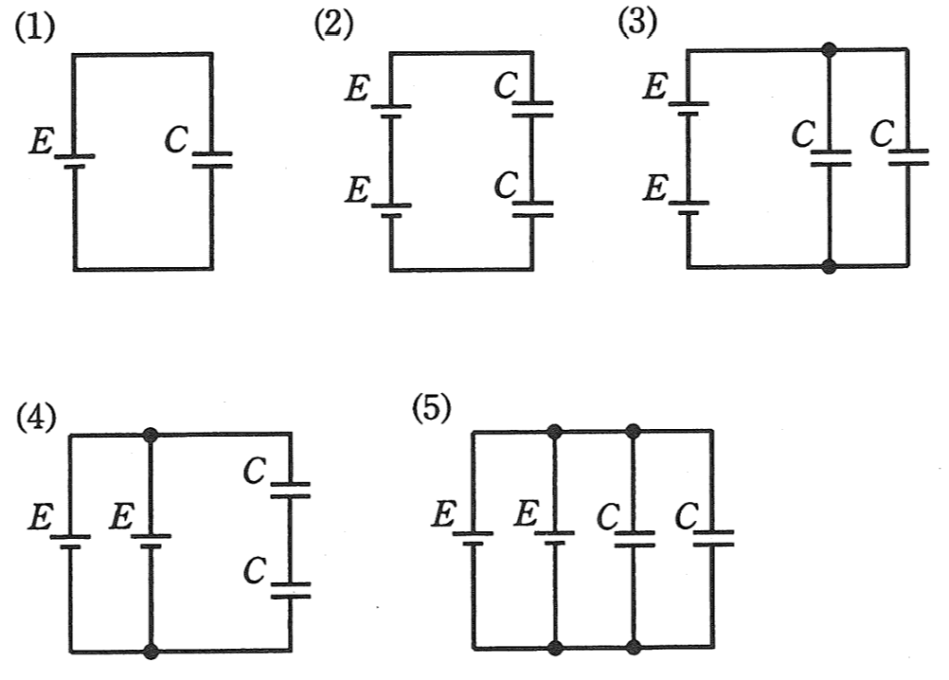
図に示す５種類の回路は、直流電圧\(E[V]\)の電源と静電容量\(C[F]\)の
コンデンサの個数と組み合わせを異にしたものである。
これらの回路のうちで、コンデンサ全体に蓄えられている電界のエネルギーが最も小さい回路を示す図
として、正しいのは次のうちどれか。

回答

答え

(4)

回答方針

電源の直列・並列接続時のそれぞれの特性、コンデンサの直列・並列接続時のそれぞれの特性について理解することが重要です。

要点整理

電源の直並列時の特性について比較します。

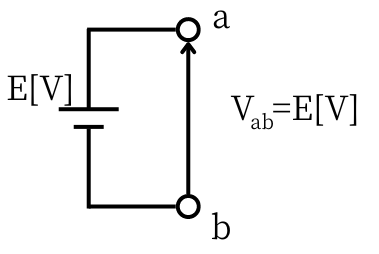	電圧\(E[V]\)の直流電源が１つだけある時 点aと、点bの両端に現れる電圧は\(V_{ab}=E[V]\)です。
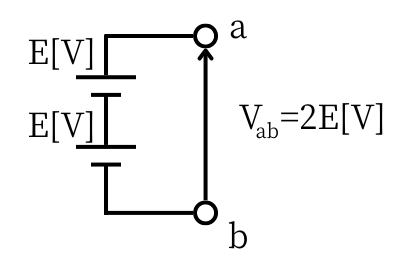	電圧\(E[V]\)の直流電源が２つ直列接続されている時 点aと、点bの両端に現れる電圧は\(V_{ab}=E+E=2E[V]\)です。
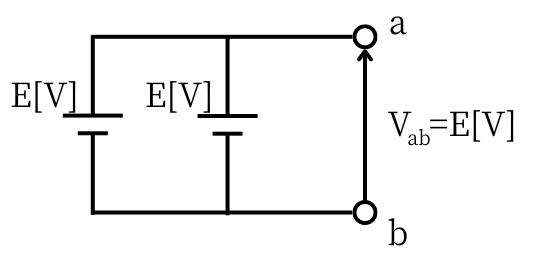	電圧\(E[V]\)の直流電源が２つ並列接続されている時 点aと、点bの両端に現れる電圧は\(V_{ab}=E[V]\)です。

コンデンサの直並列時の特性について比較します。

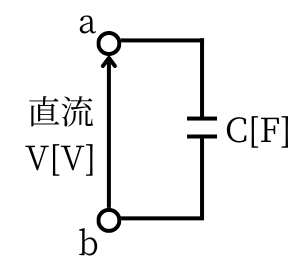	静電容量\(C[F]\)のコンデンサが１つだけある時の静電容量は、\(C[F]\)です。 電圧\(V[V]\)を印加しているとき、コンデンサに蓄えられる電界のエネルギー\(W[J]\)は、 \(\displaystyle W=\frac{1}{2}CV^2[J]\) です。
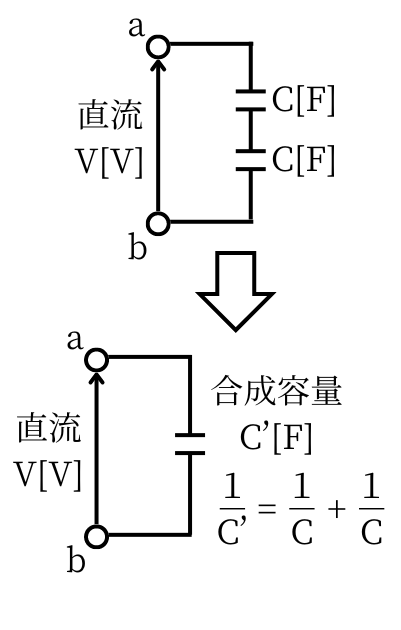	静電容量\(C[F]\)のコンデンサが２つ直列接続されている時の合成容量は \(\displaystyle \frac{1}{C^{‘}}=\frac{1}{C}+\frac{1}{C}=\frac{2}{C}[F]\) なので、 \(\displaystyle C^{‘}=\frac{1}{2}C[F]\) です。 電圧\(V[V]\)を印加しているとき、コンデンサに蓄えられる電界のエネルギー\(W[J]\)は、 \(\displaystyle W=\frac{1}{2}C^{‘}V^2=\frac{1}{4}CV^2[J]\) です。
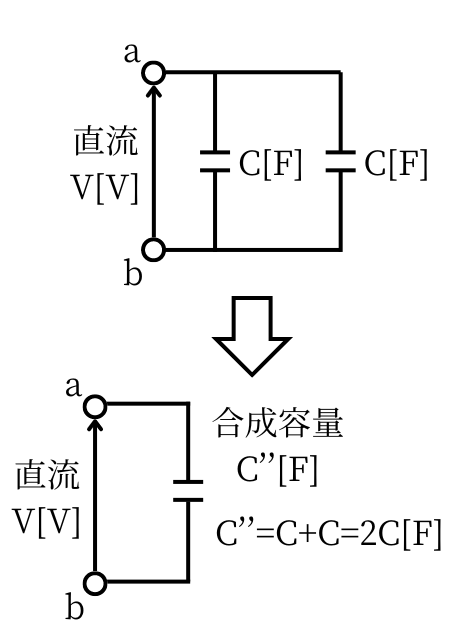	静電容量\(C[F]\)のコンデンサが２つ並列接続されている時の合成容量は \(\displaystyle C^{”} =C+C =2C[F]\) です。 電圧\(V[V]\)を印加しているとき、コンデンサに蓄えられる電界のエネルギー\(W[J]\)は、 \(\displaystyle W=\frac{1}{2}C^{”}V^2=CV^2[J]\) です。

要点整理の適用

(1)

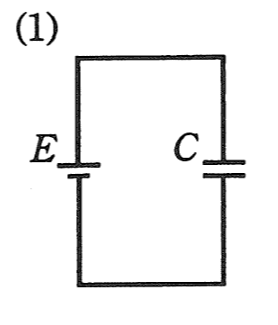	コンデンサ\(C\)に印加される直流電圧は\(E\)なので、 コンデンサに蓄えられる電界のエネルギーは \(\displaystyle W_1=\frac{1}{2}CE^2\)
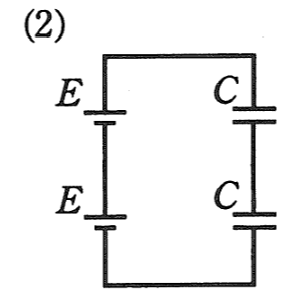	２つの直列接続されたコンデンサ\(C\)の静電容量は、 \(\displaystyle C’=\frac{1}{2}C\) ２つの直列接続された電源\(E\)の合成電圧は、 \(E’=2E\) したがって、コンデンサに蓄えられる電界のエネルギーは \(\displaystyle W_2=\frac{1}{2}C’ E’^2=CE^2\)
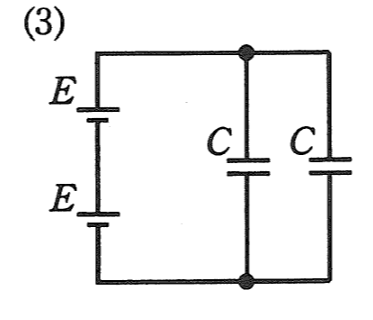	２つの並列接続されたコンデンサ\(C\)の静電容量は、 \(\displaystyle C’=2C\) ２つの直列接続された電源\(E\)の合成電圧は、 \(E’=2E\) したがって、コンデンサに蓄えられる電界のエネルギーは \(\displaystyle W_2=\frac{1}{2}C’E’^2=4CE^2\)
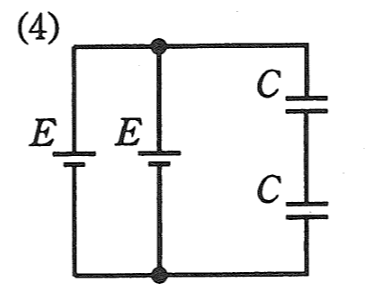	２つの直列接続されたコンデンサ\(C\)の静電容量は、 \(\displaystyle C’=\frac{1}{2}C\) ２つの並列接続された電源\(E\)の合成電圧は、 \(E’=E\) したがって、コンデンサに蓄えられる電界のエネルギーは \(\displaystyle W_2=\frac{1}{2}C’E’^2=\frac{1}{4}CE^2\)
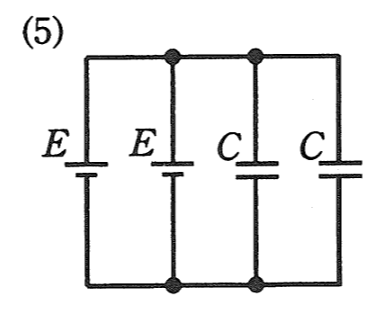	２つの並列接続されたコンデンサ\(C\)の静電容量は、 \(\displaystyle C’=2C\) ２つの並列接続された電源\(E\)の合成電圧は、 \(E’=E\) したがって、コンデンサに蓄えられる電界のエネルギーは \(\displaystyle W_2=\frac{1}{2}C’E’^2=CE^2\)

以上より、コンデンサに蓄えられる電界エネルギーが最も小さい回路は(4)です。

出典元

平成２１年度第三種電気主任技術者試験　理論科目Ａ問題問５

参考書