hパラメータとは
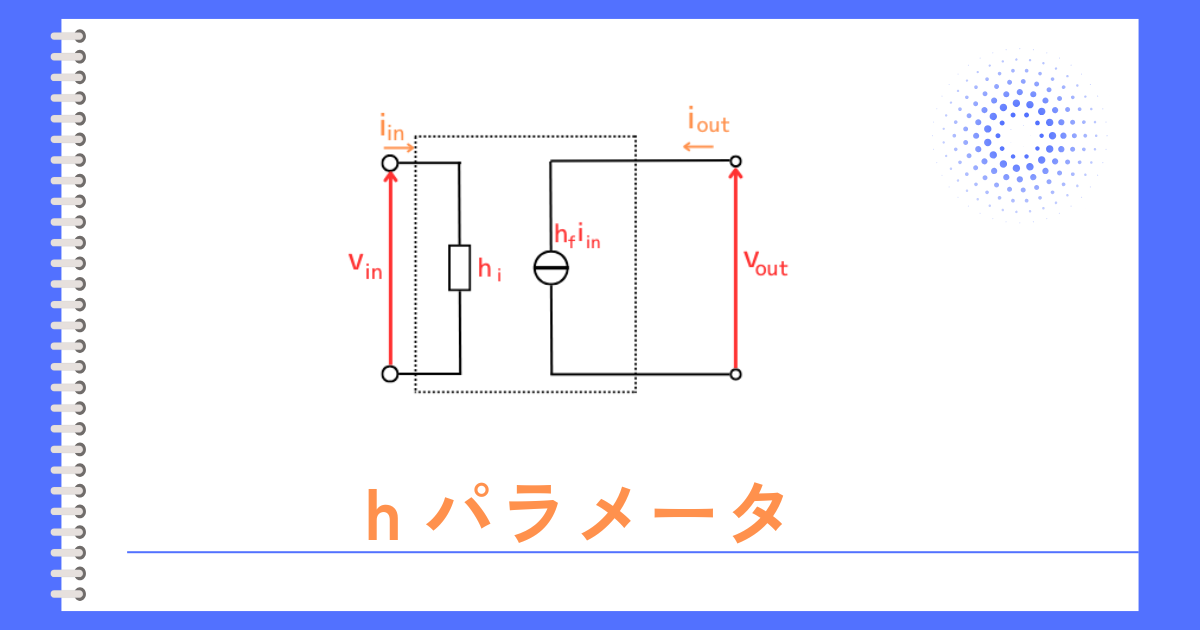
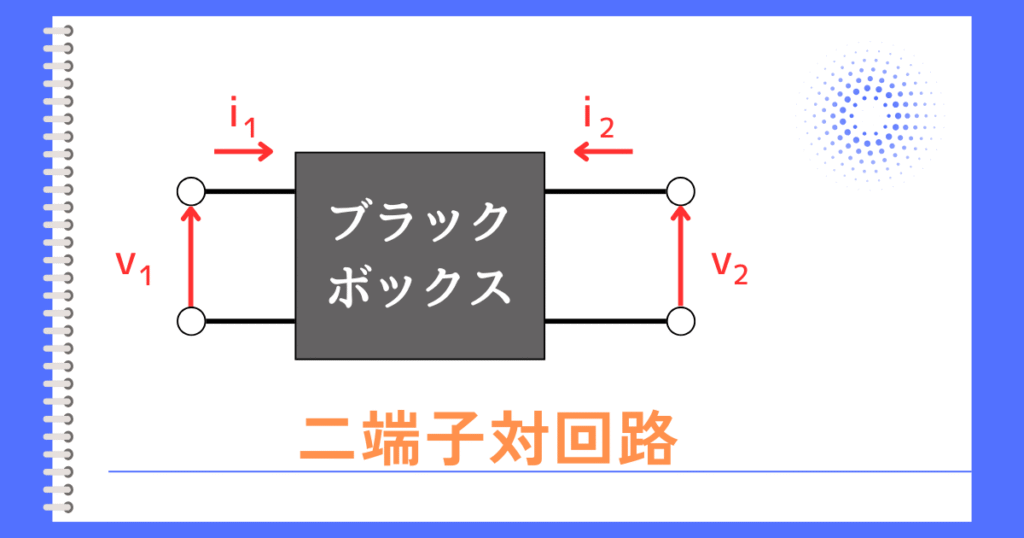
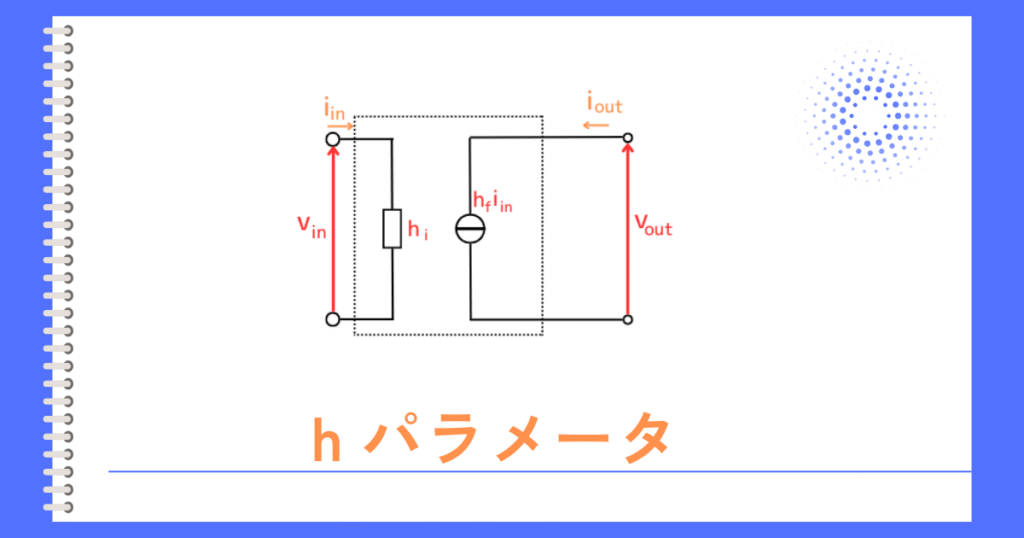
hパラメータは、入力と出力の電流電圧の関係さえわかれば、その回路特性が分かることを使って回路を簡単なモデル化した二端子対回路の表現方法の一つです。
hパラメータのhは、hパラメータの係数にインピーダンス\(Z\)とアドミタンス\(Y\)が混ざっていることから、ハイブリッド(Hybrid)という言葉が使われています。
hパラメータは、小信号増幅回路を考えるときに適した表現方法であることから、電子回路の解析でよく使われます。
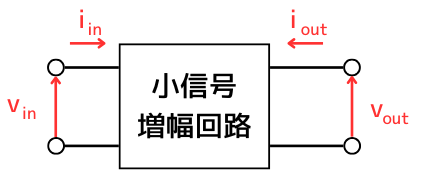
hパラメータの回路は、次のように行列で表されます。
\(\begin{bmatrix}v_{in} \\ i_{out} \end{bmatrix}=\begin{bmatrix}h_i && h_r \\h_f && h_o \end{bmatrix}\begin{bmatrix}i_{in} \\ v_{out} \end{bmatrix}\)
hパラメータの各パラメータの意味
| hパラメータ | 添え字 の意味 | hパラメータの意味 | 式 |
|---|---|---|---|
| \(h_i\) | 入力 i=input | 入力インピーダンス | \(\displaystyle h_i=\frac{v_{in}}{i_{in}}\) (\(v_{out}=0\)のとき) |
| \(h_r\) | 逆方向 r=reverse | 電圧帰還率 | \(\displaystyle h_r=\frac{v_{in}}{v_{out}}\) (\(i_{in}=0\)のとき) |
| \(h_f\) | 順方向 f=forward | 電流増幅率 | \(\displaystyle h_f=\frac{i_{out}}{i_{in}}\) (\(v_{out}=0\)のとき) |
| \(h_o\) | 出力 o=output | 出力アドミタンス | \(\displaystyle h_o=\frac{i_{out}}{v_{out}}\) (\(i_{in}=0\)のとき) |
簡易小信号等価回路
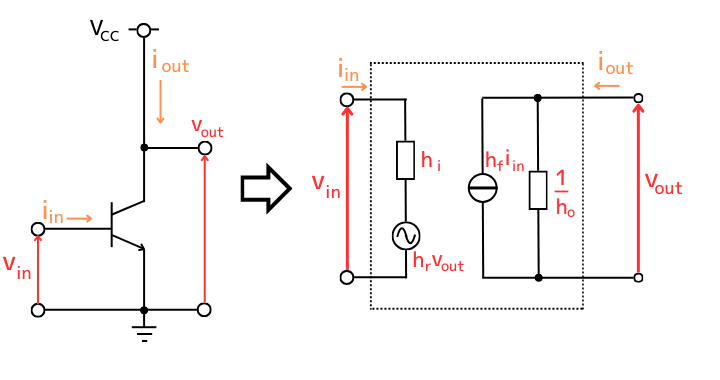
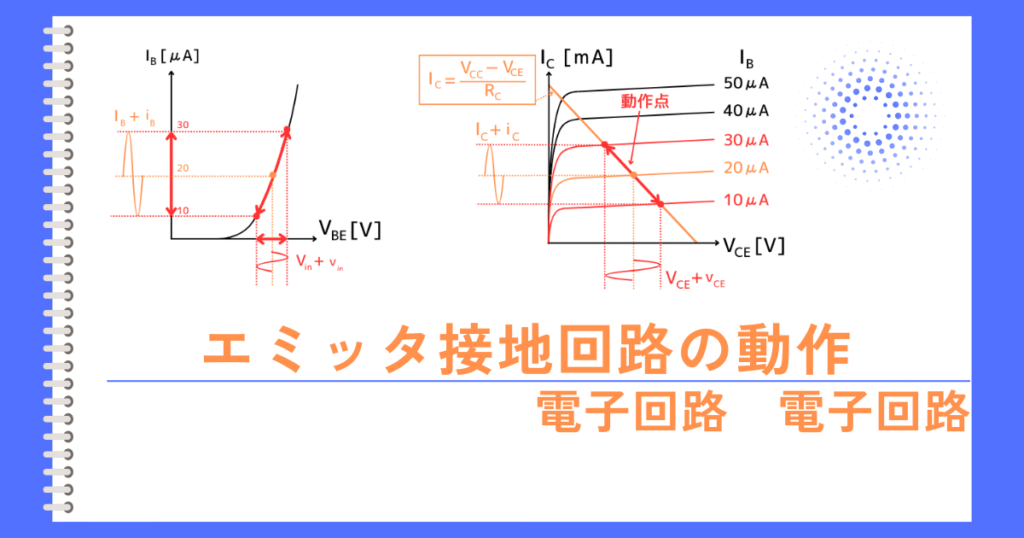
トランジスタのエミッタ接地回路は、hパラメータを使って簡易小信号等価回路に変換することで計算しやすくなります。
変換した後の入力電圧\(v_{in}\)と出力電流\(i_{out}\)の式は、次の通りです。
\(\begin{eqnarray} \left\{
\begin{array}{l}
v_{in}=h_i i_{in}+h_r v_{out} \\
i_{out}=h_f i_{in}+h_o v_{out}
\end{array}
\right.
\end{eqnarray}\)
この式を、簡易小信号等価回路として図示します。
まずは、負荷抵抗やコレクタ抵抗等があると煩雑になるので、トランジスタ単体で図示します。
回路の簡素化
トランジスタの動作は、微小な入力電流・入力電圧を増幅して、大きな出力電流・出力電圧とすることです。このことから、hパラメータは大きいパラメータと、小さいパラメータにわかれます。
大きいパラメータ
・\(h_i\):入力インピーダンス
・\(h_f\):電流増幅率
小さいパラメータ
・\(h_r\):電圧帰還率
・\(h_o\):出力アドミタンス
小さいパラメータは計算上ほとんど寄与しないため、無視できる場合が多いです。
無視できると、簡易小信号等価回路も、計算も簡素化することができます。
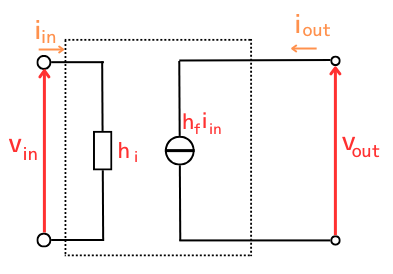
\(\begin{eqnarray} \left\{
\begin{array}{l}
v_{in}=h_i i_{in} \\
i_{out}=h_f i_{in}
\end{array}
\right.
\end{eqnarray}\)
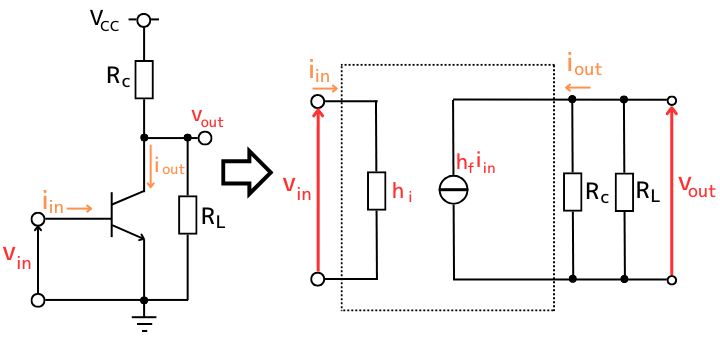
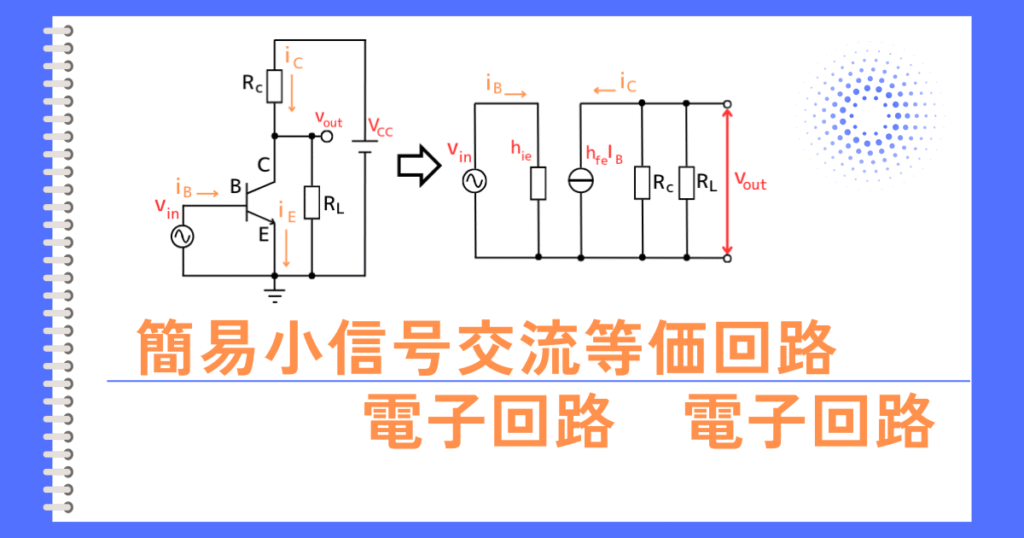
コレクタ抵抗\(R_c\)、負荷抵抗\(R_L\)も考慮した回路
コレクタ抵抗\(R_c\)、負荷抵抗\(R_L\)も合わせると、次のようになります。
トランジスタの入出力の式
\(\begin{eqnarray} \left\{
\begin{array}{l}
v_{in}=h_i i_{in} …①\\
i_{out}=h_f i_{in} …②
\end{array}
\right.
\end{eqnarray}\)
入力電流\(i_{in}\)は①式から、
\(\displaystyle i_{in}=\frac{v_{in}}{h_i}\) …③
出力インピーダンス\(R_o\)は、\(R_c\)と\(R_L\)の並列接続なので、
\(\displaystyle R_o=\frac{R_cR_L}{R_c+R_L}\) …④
出力電圧\(v_{out}\)は、出力端子のオームの法則の式から求められます。
\(\displaystyle v_{out}=R_o i_{out}=\frac{R_cR_L}{R_c+R_L}h_f i_{in}\) (②・④式を代入)
⇔\(\displaystyle v_{out}=\frac{R_cR_L}{R_c+R_L} \frac{h_f}{h_i}v_{in}\) (③式を代入)
以上の計算結果から、電圧増幅率\(A_v\)は、次のように求まります。
\(\displaystyle A_v=|\frac{v_{out}}{v_{in}}|=\frac{R_cR_L}{R_c+R_L} \frac{h_f}{h_i}\)
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント