ドリフト電流
ドリフトとは
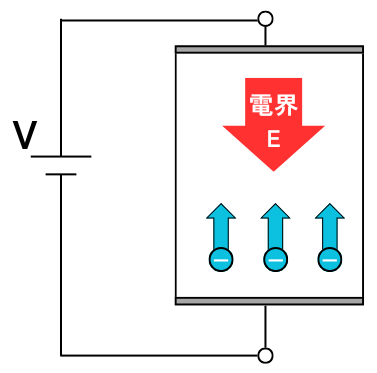
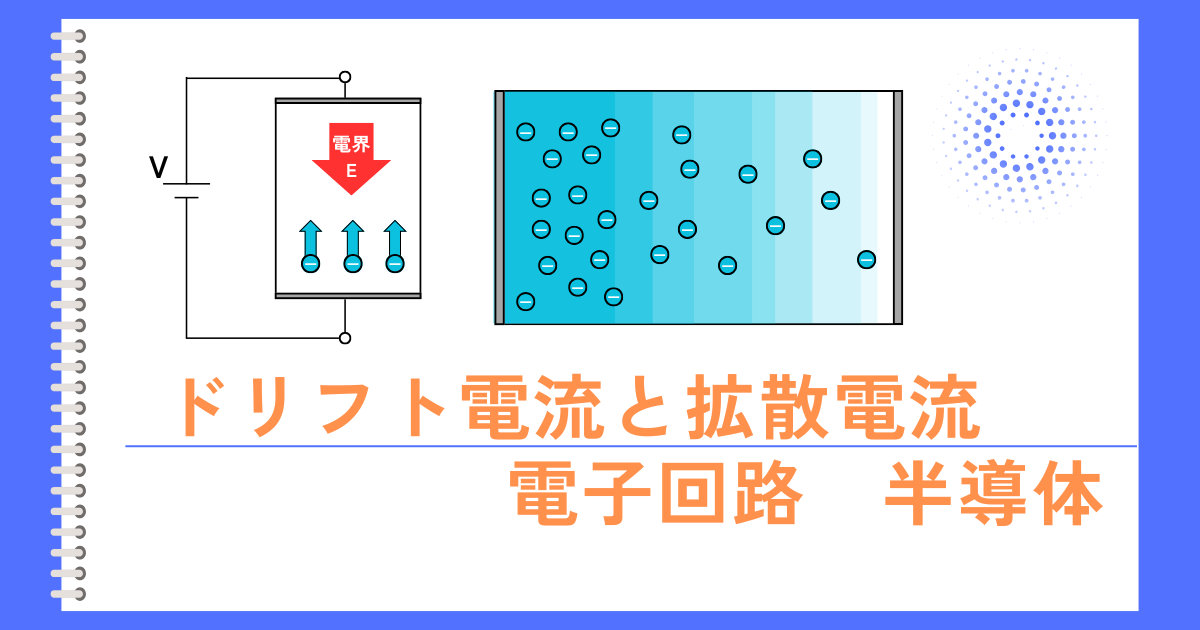
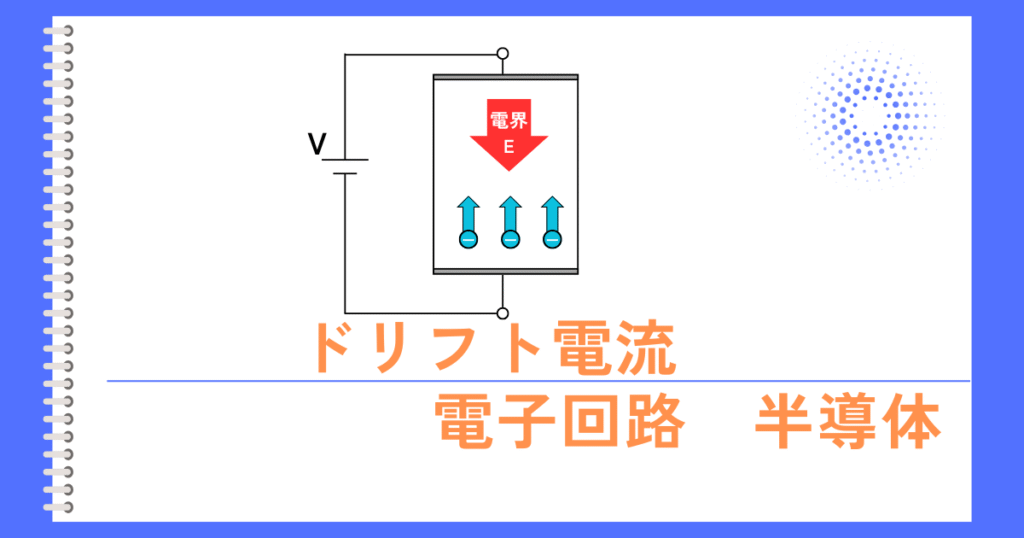
半導体に電源を接続すると、電界がかかります。
そして、かかった電界によってキャリア(正孔・電子)が移動します。
電界によってキャリアが移動する現象を、ドリフトと呼びます。
ドリフト電流とは
ドリフトによってキャリアが移動することで流れる電流のことです。
ドリフト電流は、キャリアと電界の向きによって電流の向きが決まります。
キャリアが正孔のP半導体は、正孔は正電荷であることから、電界の向きと同じ方向に電流が流れます。
キャリアが電子のN半導体は、電子は負電荷であることから、電界の向きと逆方向に電流が流れます。
キャリアの散乱
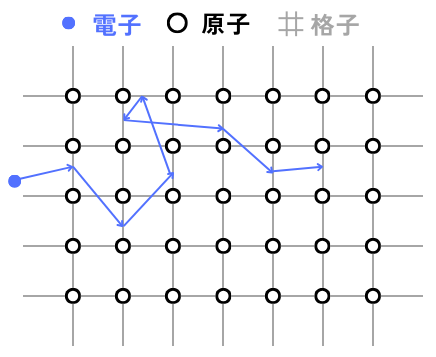
キャリアが半導体を移動すると散乱という現象が起こります。
散乱が起こると、キャリアの移動度が低下し、電気伝導率が低下します。
散乱の種類は、主にニ種類あります。
- フォノン散乱
原子は熱エネルギーによって熱振動をしています。格子振動と呼び、温度が高くなると大きくなります。
電子は、格子振動のエネルギーを受けてランダムな方向に移動します。
格子振動は熱エネルギーによる原子の振動なので、低温時はフォノン散乱の影響は小さいですが、温度が高くなるにつれてフォノン散乱の影響力が大きくなります。 - 不純物散乱
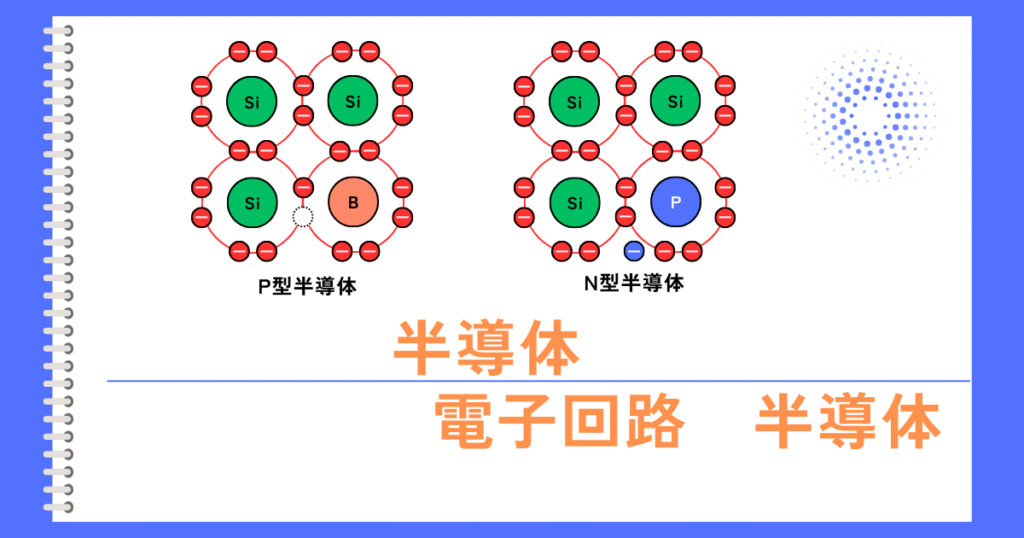
イオン化した不純物が、電子にクーロン力の影響を与えることで起こる散乱です。
低温時はキャリアの移動が遅く、クーロン力の影響を受けやすいため、不純物散乱の影響力が大きいです。
高温になるにつれて、キャリアの移動が速くなるため、クーロン力の影響を受けづらくなります。その結果、不純物散乱の影響が弱くなっていきます。
移動度
移動度は、キャリアの移動のしやすさを表します。
ドリフト電流中のキャリアの平均移動速度をドリフト速度\(v\)と呼びます。
電界強度\(E\)の電界を加えたとき、ドリフト速度\(v\)と電界強度\(E\)は比例関係となります。
このときの比例定数\(μ\)を移動度と呼び、これらの関係は次式で表されます。
\(v=μE\)
ドリフト電流密度の大きさ
電子の速度を移動度で表すことができたので、電子のドリフト電流密度\(J_n\)を定義式から展開していくと、移動度を使って表すことができます。
\(\displaystyle J_n=\frac{I}{S}=\frac{ΔQ}{SΔt}=\frac{-qnSv_nΔt}{SΔt}=-qnv_n=qnμ_nE\) …①
補足1:①式中の電流\(I\)は、電流の定義式から次式で表されます。
\(I=\frac{ΔQ}{Δt}\)
\(ΔQ\):電荷量
\(Δt\):時間
補足2:①式中の電荷量\(ΔQ\)は、次式で表されます。
\(ΔQ=-qnSv_n\)
\(q\):電子1個の電気量である電気素量
\(n\):電子の密度
\(S\):断面積
\(v_n\):電子の移動平均速度
正孔のドリフト電流密度\(J_p\)は、同様に移動度\(μ_p\)を使って表すことができます。
\(\displaystyle J_p=\frac{I}{S}=\frac{ΔQ}{SΔt}=\frac{qpSv_pΔt}{SΔt}=qpv_p=qpμ_pE\) …②
ドリフト電流密度\(J\)は、電子のドリフト電流密度\(J_n\)と正孔のドリフト電流密度\(J_p\)を合算することで求められます。(①式+②式)
\(J=J_n+J_p=q(nμ_n+pμ_p)E\) …③
なお、電流密度\(J\)、電気伝導率\(σ\)と電界強度\(E\)は、次式の関係があります。
\(J=σE\) …④
③・④式から
\(J=q(nμ_n+pμ_p)E=σE\)
拡散電流
拡散とは
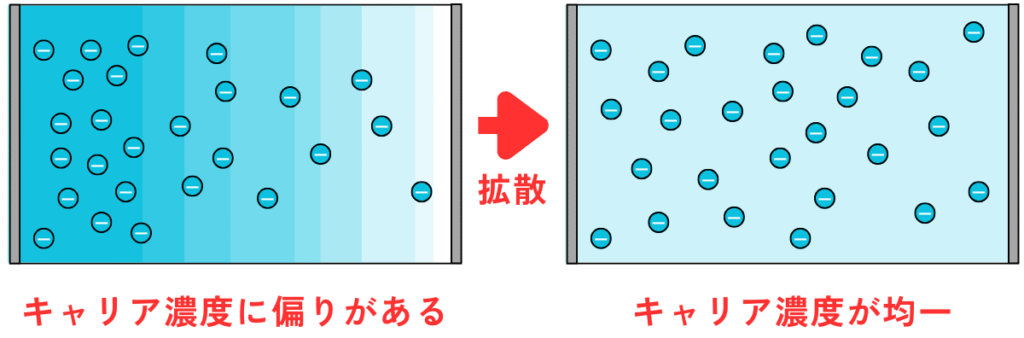
拡散とは、半導体のキャリア濃度の分布に偏りがあるとき、その濃度差を均一にするようにキャリアが移動します。
拡散電流とは
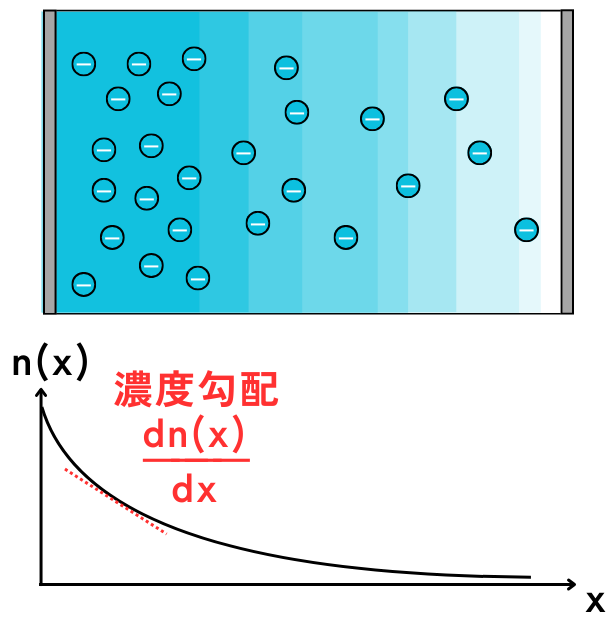
キャリアの拡散によって流れた電流を、拡散電流と呼びます。
拡散電流の大きさは、濃度勾配に比例します。
電子の拡散電流密度の式は次式で表されます。
\(\displaystyle J_n=qD_n\frac{dn}{dx}\)
正孔の拡散電流密度の式は次式で表されます。
\(\displaystyle J_p=-qD_p\frac{dp}{dx}\)
全体の拡散電流は電子と正孔による拡散を合わせた電流なので、全体の拡散電流密度は以下のように示されます。
\(\displaystyle J=J_{Dn}+J_{Dp}=q \left\{ D_n\frac{dn}{dx}-D_p\frac{dp}{dx} \right\} \)
\(J_n\):電子による拡散電流密度
\(J_p\):正孔による拡散電流密度
\(q\):電荷量
\(n\):電子のキャリア密度
\(p\):正孔のキャリア密度
\(D_n\):電子の拡散係数
\(D_p\):正孔の拡散係数
ドリフト電流と拡散電流
pn接合の接合部付近では、n型半導体のキャリアである電子と、p型半導体のキャリアである正孔が打ち消し合い消滅し、キャリアの存在しない空乏層が発生します。
この状態になると、n型半導体の電子の一部はp型半導体に拡散し、p型半導体の正孔の一部はn型半導体に拡散します。
このことにより、p型半導体はマイナスの電気を帯び、n型半導体はプラスの電気を帯びます。
このため、n型半導体からp型半導体に向かって電界が発生しますので、ドリフト電流がn型半導体からp型半導体に流れます。
拡散電流とドリフト電流が互いに打ち消し合って平衡状態になります。
このとき、ドリフト電流の式と、拡散電流の式は等しくなります。
\(\displaystyle qn(x)μE=qD\frac{dn(x)}{dx}\)
\(q\):電荷量
\(μ\):キャリアの移動度
\(E\):電界強度
\(n\):キャリアの密度
\(D\):キャリアの拡散係数
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント