合成抵抗とは
二つ以上の抵抗を電源に接続すると、電源から見た抵抗値は、全ての抵抗値を合成した抵抗値となります。
接続方法には、直列接続、並列接続の二つの接続方法があり、この違いによって、合成抵抗値・各抵抗の電圧・電流値が異なってきます。
直列接続の場合は、合成抵抗値が各抵抗値よりも大きくなります。
並列接続の場合は、合成抵抗値が各抵抗値よりも小さくなります。
これは、直列接続の場合は、電源から送られた電流が通りづらい抵抗を2回通らなければならないのに対し、並列接続の場合は、電流が通りやすい方の抵抗を通ることができるためです。
公式一覧
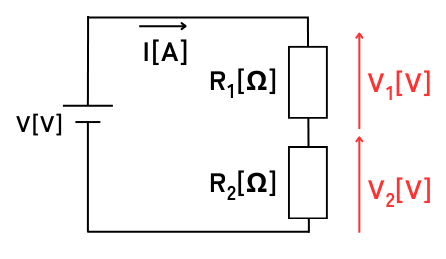
直列接続時の各抵抗にかかる電圧\(V_1[V]\)、\(V_2[V]\)
\(\displaystyle V_1=\frac{R_1}{R_1+R_2}V\)
\(\displaystyle V_2=\frac{R_2}{R_1+R_2}V\)
直列接続時の各抵抗に流れる電流\(I[A]\)
全ての抵抗に \(\displaystyle I=\frac{V}{R}\) の電流が流れる。
直列接続時の合成抵抗\(R[Ω]\)
\(R=R_1+R_2\)
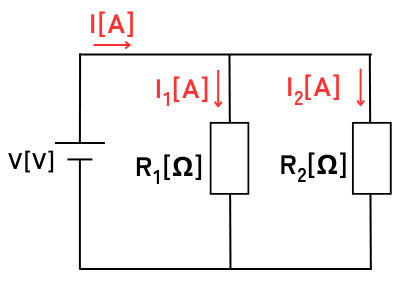
並列接続時の各抵抗にかかる電圧
全て\(V[V]\)が印加される。
並列接続時の各抵抗に流れる電流\(I_1\)、\(I_2\)
\(\displaystyle I_1=\frac{R_2}{R_1+R_2}I\)
\(\displaystyle I_2=\frac{R_1}{R_1+R_2}I\)
並列接続時の合成抵抗\(R[Ω]\)
\(\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\)
直列接続
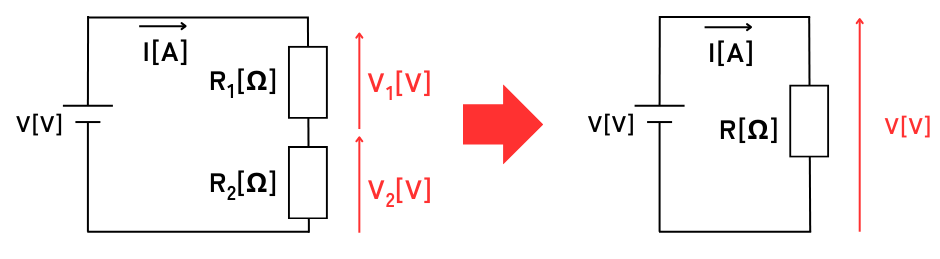
直列接続時の各抵抗にかかる電圧\(V_1[V]\)、\(V_2[V]\)
\(\displaystyle V_1=\frac{R_1}{R_1+R_2}V\)
\(\displaystyle V_2=\frac{R_2}{R_1+R_2}V\)
直列接続時の各抵抗に流れる電流\(I[A]\)
全ての抵抗に \(\displaystyle I=\frac{V}{R}\) の電流が流れる。
直列接続時の合成抵抗\(R[Ω]\)
\(R=R_1+R_2\)
直列の合成抵抗の導出
抵抗の直列接続時の電流は、キルヒホッフの電流則から入ってくる電流と、出て行く電流が等しいです。そのため、各抵抗\(R_1\)、\(R_2\)に流れる電流は両方とも\(I[A]\)です。
閉回路の電源による起電力と、負荷の電圧降下は等しいという、キルヒホッフの電圧則から、次の②式が成り立ちます。
\(V=V_1+V_2\) …①
オームの法則から、
\(V=IR\) …②
\(V_1=IR_1\) …③
\(V_2=IR_2\) …④
①式に②~④式を代入すると、
\(IR=IR_1+IR_2\)
⇔\(R=R_1+R_2\)
以上より、直列接続時の合成抵抗\(R=R_1+R_2\)が導出できました。
直列抵抗の分圧の導出
各抵抗\(R_1\)、\(R_2\)に流れる電流は両方とも\(I[A]\)です。
\(I\)は、オームの法則から、①式で表されます。
\(\displaystyle I=\frac{V}{R}=\frac{V}{R_1+R_2}\) …①
抵抗\(R_1[Ω]\)に印加される電圧\(V_1[V]\)は、オームの法則から、②式のように導出できます。
\(\displaystyle V_1=IR_1=\frac{R_1}{R_1+R_2}V\) …②
抵抗\(R_2[Ω]\)に印加される電圧\(V_2[V]\)は、オームの法則から、③式のように導出できます。
\(\displaystyle V_2=IR_2=\frac{R_2}{R_1+R_2}V\) …③
以上、②・③式から、直列抵抗の分圧式が導出できました。
並列接続
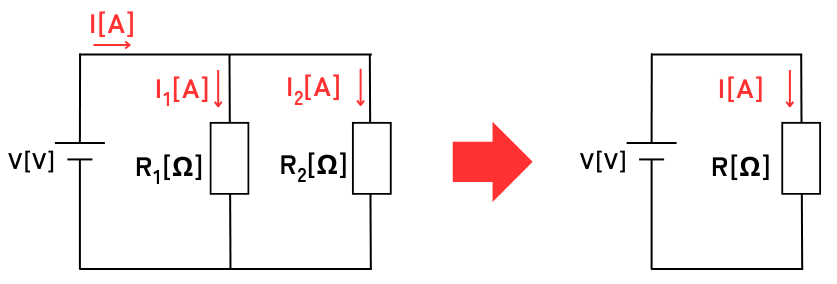
並列接続時の各抵抗にかかる電圧\(V[V]\)
全ての抵抗に\(V\)が印加される。
並列接続時の各抵抗に流れる電流\(I_1[A]\)、\(I_2[A]\)
\(\displaystyle I_1=\frac{R_2}{R_1+R_2}I\)
\(\displaystyle I_2=\frac{R_1}{R_1+R_2}I\)
並列接続時の合成抵抗\(R[Ω]\)
\(\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\)
並列の合成抵抗の導出
各抵抗\(R_1\)、\(R_2\)に印加される電圧は、両方とも\(V[V]\)です。
各抵抗に流れる電流\(I_1[A]\)、\(I_2[A]\)は、オームの法則から、
\(\displaystyle I_1=\frac{V}{R_1}\) …①
\(\displaystyle I_2=\frac{V}{R_2}\) …②
合成抵抗\(R\)に印加される電圧は、\(V[V]\)です。
合成抵抗\(R\)に流れる電流\(I[A]\)は、オームの法則から
\(\displaystyle I=\frac{V}{R}\) …③
キルヒホッフの電流則から入ってくる電流と、出て行く電流が等しくなるので、
\(I=I_1+I_2\) …④
④式に①・②・③式を代入すると、
\(\displaystyle \frac{V}{R}=\frac{V}{R_1}+\frac{V}{R_2}\)
⇔\(\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\)
以上より、並列接続時の合成抵抗\(\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\)が導出できました。
並列抵抗の分路電流の導出
合成抵抗\(R\)に流れる電流\(I[A]\)は、オームの法則から、
\(\displaystyle I=\frac{V}{R}\) …①
合成抵抗\(R\)を計算すると、
\(\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{R_1+R_2}{R_1 R_2}\) …②
①式に②式を代入すると、
\(\displaystyle I=\frac{R_1+R_2}{R_1 R_2}V\) …③
各抵抗\(R_1\)、\(R_2\)に流れる電流\(I_1[A]\)、\(I_2[A]\)は、オームの法則から、
\(\displaystyle I_1=\frac{V}{R_1}\) …④
\(\displaystyle I_2=\frac{V}{R_2}\) …⑤
まずは、抵抗\(R_1\)に流れる電流\(I_1[A]\)から求めて行きます。
キルヒホッフの電流則から入ってくる電流と、出て行く電流が等しくなるので、
\(I=I_1+I_2\)
⇔ \(I_1=I-I_2\) …⑥
⑥式に③・⑤式を代入すると、
\(\displaystyle \begin{eqnarray}
I_1&=&I-I_2=\frac{R_1+R_2}{R_1 R_2}V-\frac{V}{R_2}=\frac{R_1+R_2}{R_1 R_2}V-\frac{R_1}{R_1 R_2}V=\frac{R_2}{R_1 R_2}V
\end{eqnarray}\)
次に、抵抗\(R_2\)に流れる電流\(I_2[A]\)を同様に求めると、
\(\displaystyle \begin{eqnarray}
I_2&=&I-I_1=\frac{R_1+R_2}{R_1 R_2}V-\frac{V}{R_1}=\frac{R_1+R_2}{R_1 R_2}V-\frac{R_2}{R_1 R_2}V=\frac{R_1}{R_1 R_2}V
\end{eqnarray}\)
以上より、並列抵抗の分路電流\(\displaystyle I_1=\frac{R_2}{R_1 R_2}V\)、\(\displaystyle I_2=\frac{R_1}{R_1 R_2}V\)が導出できました。
過去問
難易度 ★☆☆☆☆
| 電験三種 令和5年度下期 問5 | 直並列接続された抵抗の消費電力の計算 |
| 電験三種 令和5年度下期 問7 | 回路条件切替による抵抗値の計算 |
| 電験三種 平成21年度 問6 | 直並列回路の抵抗値の計算 |
難易度 ★★☆☆☆
| 電験三種 令和5年度上期 問6 | 電圧源・電流源からなる2電源回路の解析 |
関連記事(直流回路に関する解説)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント