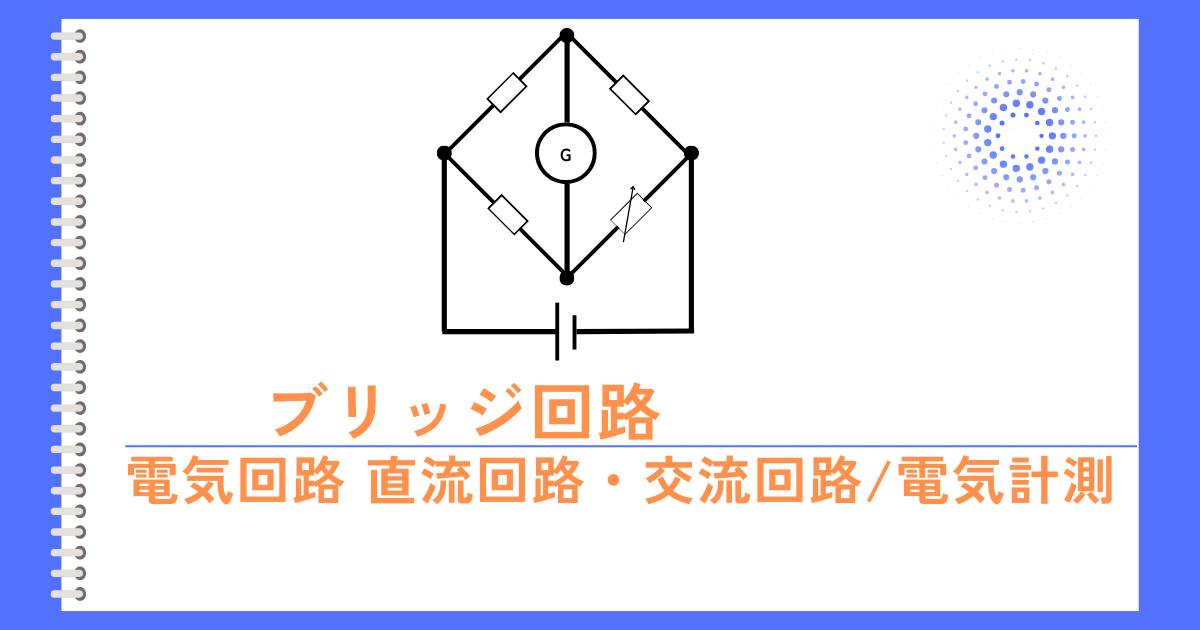
ブリッジ回路とは
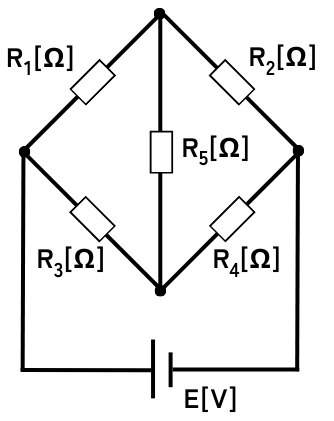
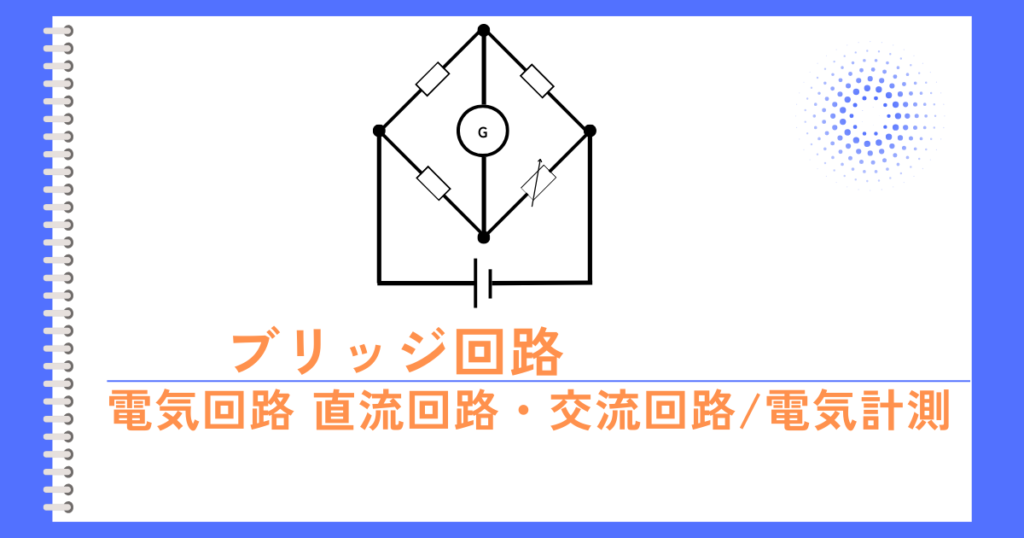
ブリッジ回路は、左図のように4つの素子を橋渡すような形状にした電気回路です。
\(R_1R_4=R_2R_3\)の式が成り立つとき、抵抗\(R_5\)に流れる電流は\(0A\)です。この状態を平衡状態と呼びます。
この平衡状態を使うことで、抵抗値の精密測定や、ひずみゲージ等に応用されます。
平衡状態の原理
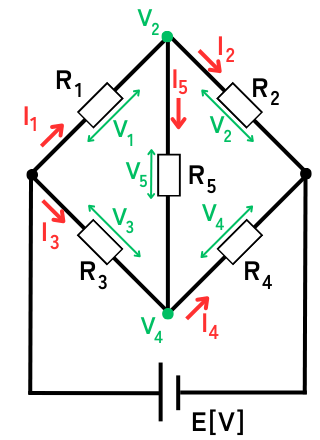
左図のようなブリッジ回路があったとします。
平衡状態であるとき、抵抗\(R_5\)に流れる電流は\(I_5=0A\)、電流が流れないということは、電圧も\(V_5=0V\)となります。
したがって、平衡状態が出来る条件は、\(V_2\)と、\(V_4\)が同電位であることです。
\(V_2=V_4\) …①
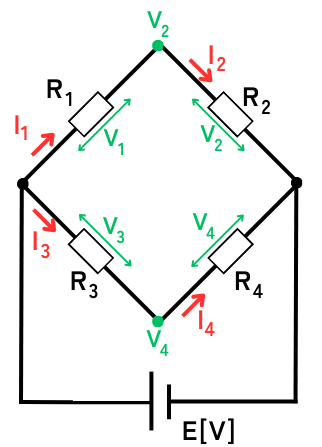
平衡状態のとき、抵抗\(R_5\)には電流が流れないことから、\(R_5\)を除去して回路を簡単化できます。
この状態であれば、\(V_2\)、\(V_4\)は直列抵抗の分圧式から簡単に導き出せます。
\(\displaystyle V_2=\frac{R_2}{R_1+R_2}E\) …②
\(\displaystyle V_4=\frac{R_4}{R_3+R_4}E\) …③
①式に②・③式を代入すると、
\(\displaystyle \frac{R_2}{R_1+R_2}E=\frac{R_4}{R_3+R_4}E\)
⇔\(R_2(R_3+R_4)=R_4(R_1+R_2)\)
⇔\(R_2R_3=R_1R_4\)
したがって、\(R_2R_3=R_1R_4\)が成り立つとき、平衡状態となります。
直流ブリッジ回路(ホイートストンブリッジ)
回路の目的
ホイートストンブリッジ回路は、抵抗を高精度に測定する回路です。
回路の構成と原理
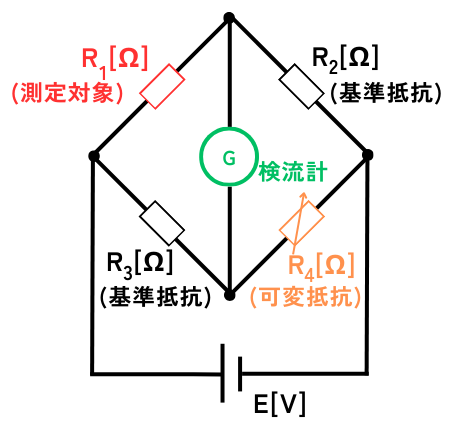
・測定対象\(R_1\)
・抵抗\(R_2\)、\(R_3\)
・可変抵抗\(R_4\)
をブリッジ状に接続して、ブリッジ回路の真ん中に、電流がわずかにでも流れると針が振れる検流計を接続することで構成されます。
可変抵抗を調整して、検流計の針が振れなくなったときが、ブリッジ回路が平衡になったときです。
このときの3つの抵抗を読み取ることで、次式で測定対象の抵抗値がわかります。
\(\displaystyle R_1=\frac{R_2R_3}{R_4}\)
\(R_1\)の抵抗値の式からわかるように、回路の電源電圧や、回路中に流れる電流に依存しないため、高精度の抵抗値測定をすることが出来ます。
平衡状態になるまで、可変抵抗\(R_4\)を調節しなければならないため、測定できるまでにかなり時間がかかります。
わずかなズレでも検流計は振れるので、可変抵抗の調節はかなり面倒くさいです。
交流ブリッジ回路(電験二種の範囲)
ブリッジ回路は、直流回路だけでなく、交流回路でも幅広く使用できます。
交流回路のブリッジ回路の計算は、複素数が出てきて少々手間がかかるため、電験二種の出題範囲となります。
三種を勉強している人は、参考程度にすると良いでしょう。
シェーリングブリッジ回路
回路の目的
静電正接 \(tanδ\) を測定する回路です。
回路の構成と原理
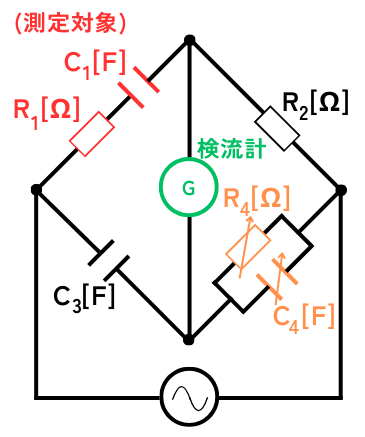
・直列接続された測定対象の抵抗\(R_1\)、容量\(C_1\)
・抵抗\(R_2\)
・容量\(C_3\)
・並列接続された可変抵抗\(R_4\)、容量\(C_4\)
をブリッジ状に接続して、ブリッジ回路の真ん中に、電流がわずかにでも流れると針が振れる検流計を接続することで構成されます。
直列接続された測定対象\(R_1\)と\(C_1\)の合成インピーダンス\(Z_1\)は、
\(Z_1=R_1+\frac{1}{jωC_1}=\frac{1+jωC_1R_1}{jωC_1}\)
並列接続された\(R_4\)と\(C_4\)の合成インピーダンス\(Z_4\)は、
\(\frac{1}{Z_4}=\frac{1}{R_4}+jωC_4\) ⇔ \(Z_4=\frac{R_4}{1+jωC_4R_4}\)
平行条件は、
\(\left( \frac{1+jωC_1R_1}{jωC_1} \right) \left( \frac{R_4}{1+jωC_4R_4} \right) = R_2・\frac{1}{jωC_3}\)
⇔\(jωC_3(1+jωC_1R_1)R_4=jωC_1(1+jωC_4R_4)R_2\)
⇔\(C_3R_4+jωC_1C_3R_1R_4=C_1R_2+jωC_1C_4R_2R_4\)
実数部から、\(C_3R_4=C_1R_2\) ⇔ \(C_1=\frac{R_4}{R_2}C_3\) …①
虚数部から、\(C_3R_1=C_4R_2\) ⇔ \(R_1=\frac{C_4}{C_3}R_2\) …②
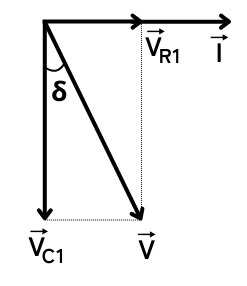
\(R_1\)の端子電圧を\(\vec{V_{R1}}\)
\(C_1\)の端子電圧を\(\vec{V_{C1}}\)
\(R_1\)・\(C_1\)の直列接続の端子電圧を\(\vec{V_1}\)
流れる電流を\(\vec{I}\)
として、ベクトル図に示すと、図のようになります。
\(|V_{R1}|=R_1I\)
\(|V_{C1}|=\frac{I}{ωC_1}\)
なので、
\(\displaystyle tanδ=\frac{|V_{R1}|}{|V_{C1}|}=\frac{R_1I}{\frac{I}{ωC_1}}=ωC_1R_1\)
①・②式を代入すると、
\(tanδ=ωC_1R_1=ω\frac{R_4}{R_2}C_3・\frac{C_4}{C_3}R_2=ωC_4R_4\)
以上より、平衡した時の周波数、可変抵抗、可変容量の値から静電正接\(tanδ\)が求まります。
ウィーンブリッジ回路
回路の目的
回路の周波数を測定する回路です。
回路の構成と原理
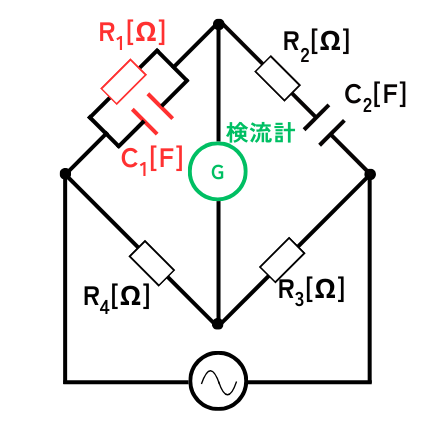
・並列接続された抵抗\(R_1\)、容量\(C_1\)
・直列接続された抵抗\(R_2\)、容量\(C_2\)
・抵抗\(R_3\)、\(R_4\)
をブリッジ状に接続して、ブリッジ回路の真ん中に、電流がわずかにでも流れると針が振れる検流計を接続することで構成されます。
並列接続された\(R_1\)と\(C_1\)の合成インピーダンス\(Z_1\)は、
\(\displaystyle \frac{1}{Z_1}=\frac{1}{R_1}+jωC_1\) ⇔ \(\displaystyle Z_1=\frac{1}{\frac{1}{R_1}+jωC_1}\)
直列接続された\(R_2\)と\(C_2\)の合成インピーダンス\(Z_2\)は、
\(Z_2=R_2+\frac{1}{jωC_2}\)
他のインピーダンスは、
\(Z_3=R_3\)
\(Z_4=R_4\)
平行条件は、
\(Z_1Z_3=Z_2Z_4\)
⇔\(\displaystyle R_3 \left( \frac{1}{\frac{1}{R_1}+jωC_1} \right)=R_4 \left( R_2+\frac{1}{jωC_2}\right)\)
⇔\(\displaystyle \frac{R_3}{R_4}=\left( \frac{1}{R_1}+jωC_1 \right) \left( R_2+\frac{1}{jωC_2}\right)\)
⇔\(\displaystyle \frac{R_3}{R_4}=\frac{R_2}{R_1}+\frac{C_1}{C_2}+jωC_1R_2+\frac{1}{jωC_2R_1}\)
実数部から
\(\displaystyle \frac{R_3}{R_4}=\frac{R_2}{R_1}+\frac{C_1}{C_2}\)
実部が成り立つ条件として、\(R_3=2R_4\)、\(R_1=R_2\)、\(C_1=C_2\)とします。
※両辺0となれば良いです。
このとき、\(2=1+1\)となり、実数部の式は成り立ちます。
虚数部から
\(\displaystyle 0=jωC_1R_2+\frac{1}{jωC_2R_1}\)
⇔ \(\displaystyle 0=j(ωC_1R_2-\frac{1}{ωC_2R_1})\)
⇔ \(\displaystyle ω^2=\frac{1}{C_1C_2R_1R_2}\)
\(ω=2πf\)を代入すると、
⇔ \(\displaystyle 2πf=\frac{1}{\sqrt{C_1C_2R_1R_2}}\)
⇔ \(\displaystyle f=\frac{1}{2π\sqrt{C_1C_2R_1R_2}}\)
実数部が成り立つ条件から、\(R_1=R_2\)、\(C_1=C_2\)を代入すると、
\(\displaystyle f=\frac{1}{2πC_1R_1}\)
以上より、ウィーンブリッジ回路が平衡したときの電源周波数は、\(\displaystyle f=\frac{1}{2πC_1R_1}\)
マクスウェルブリッジ回路
回路の目的
誘導性インピーダンス(\(Z_x=R_x+jωL_x\))を測定する回路です。
回路の構成と原理
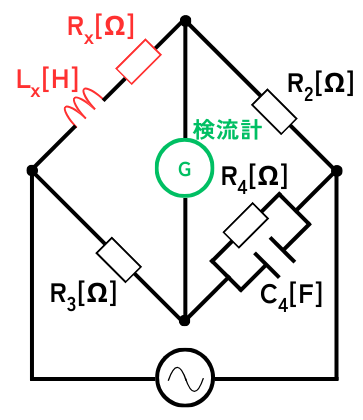
・直列接続された測定対象の抵抗\(R_x\)と、
インダクタンス\(L_x\)からなる誘導性インピーダンス\(Z_x\)
・抵抗\(R_2\)、\(R_3\)
・並列接続された抵抗\(R_4\)、容量\(C_4\)
をブリッジ状に接続して、ブリッジ回路の真ん中に、電流がわずかにでも流れると針が振れる検流計を接続することで構成されます。
直列接続された測定対象の誘導性インピーダンス\(Z_x\)は、\(R_x\)と\(L_x\)から、
\(Z_x=R_x+jωL_x\)
並列接続された\(R_4\)と\(C_4\)の合成インピーダンス\(Z_4\)は、
\(\displaystyle \frac{1}{Z_4}=\frac{1}{R_4}+jωC_4\) ⇔ \(\displaystyle Z_4=\frac{R_4}{1+jωC_4R_4}\)
他のインピーダンスは、
\(Z_2=R_2\)
\(Z_3=R_3\)
平衡条件\(Z_xZ_4=Z_2Z_3\)から、
\((R_x+jωL_x) \left( \frac{R_4}{1+jωC_4R_4} \right) =R_2R_3\)
⇔ \(R_4(R_x+jωL_x) =R_2R_3(1+jωC_4R_4)\)
⇔ \(R_4R_x+jωL_xR_4 =R_2R_3+jωC_4R_2R_3R_4\)
実数部から
\(R_4R_x=R_2R_3\)
⇔ \(\displaystyle R_x=\frac{R_2R_3}{R_4}\)
虚数部から
\(jωL_xR_4 =jωC_4R_2R_3R_4\)
⇔ \(L_x =C_4R_2R_3\)
以上より、マクスウェルブリッジ回路が平衡したときの誘導性インピーダンス\(Z_x\)の抵抗値\(R_x\)とインダクタンス\(L_x\)は、次のように求まることがわかりました。
\(\displaystyle R_x=\frac{R_2R_3}{R_4}\)
\(L_x =C_4R_2R_3\)
測定方法(零位法・偏位法)
電気計測による測定方法は、零位法と、偏位法の2つに大別されます。
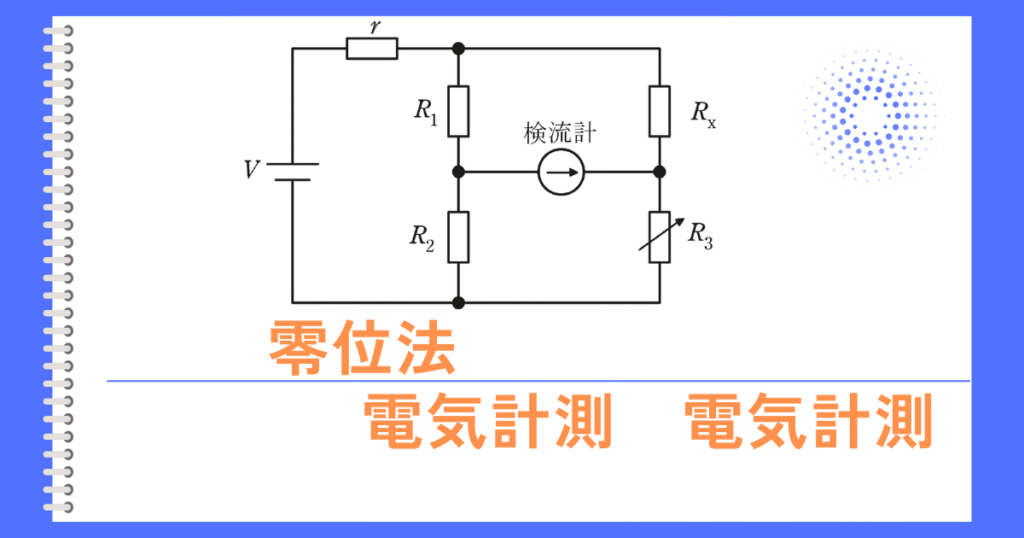
零位法
零位法とは、既にどれくらいの大きさかわかっている基準となる物と、測定対象を比較して、差を検出することで測定量を求める方法です。
この方法を使用すると、測定器の内部抵抗による影響を受けない測定ができるため、誤差が小さく、高精度な測定をすることが出来ます。
零位法の具体例は、ホイートストンブリッジ回路に代表されるブリッジ回路です。
零位法のメリット・デメリットまとめ
メリット
測定対象を高精度に測定することが可能。
デメリット
測定量と基準量が等しくなるまで調整する必要があり、測定に時間がかかる。
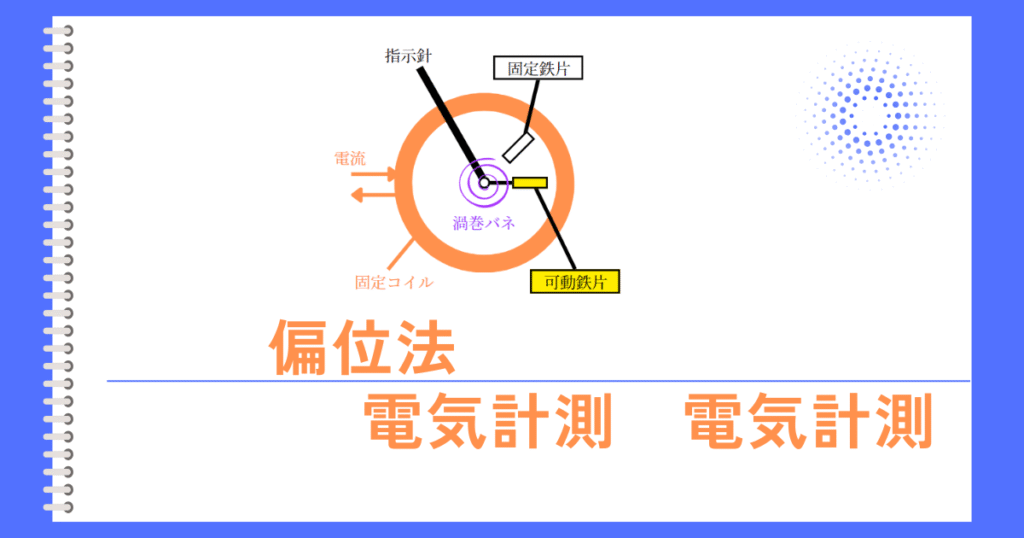
偏位法
偏位法とは、測定対象から受けた電圧、流れた電流を、直接針の振れとして変換することで測定できる方法です。
偏位法の具体例は、電圧計や、電流計等です。
この方法を使用すると、針の振れを読むだけで測定が出来るため、とても早く測定することが出来るだけでなく、時間変化するような場合でも連続して読み取ることが出来ます。
しかし、電圧計、電流計等には内部抵抗が存在するため、その内部抵抗が原因となる測定誤差が発生します。
偏位法のメリット・デメリットまとめ
メリット
①測定器の指示値を読むだけなので、測定に時間がかからない。
②測定量が時間変化しても連続的に指示できる。
デメリット
①高精度の測定をすることができない。
②測定対象の回路から電圧・電流を受けて測定するため、測定対象に影響を与える。
過去問
難易度 ★☆☆☆☆
| 電験三種 令和4年度下期 問5 | ホイートストンブリッジ回路の計算 |
関連記事
直流回路
電気計測
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント