概要
三相平衡のΔ-Y変換の計算問題です。
抵抗、インダクタンス、コンデンサが含まれる三相交流の問題なので難しそうに見えますが、三相平衡時のΔ-Y変換の導出方法さえ理解してしまえば、解答は可能です。
また、三相交流の問題では、線電流、相電流、線間電圧、相電圧の違いについての理解も必須です。
本ページの最後に、三相平衡負荷の簡単なΔ-Y変換の方法を記載しておきます。
キーワード
線電流、相電流、線間電圧、相電圧、三相平衡負荷、Y-Δ変換
問題
図1のように、相電圧200 V、周波数50 Hzの対称三相交流電源に、抵抗とインダクタンスからなる三相平衡負荷を接続した交流回路がある。次の(a)及び(b)の問に答えよ。
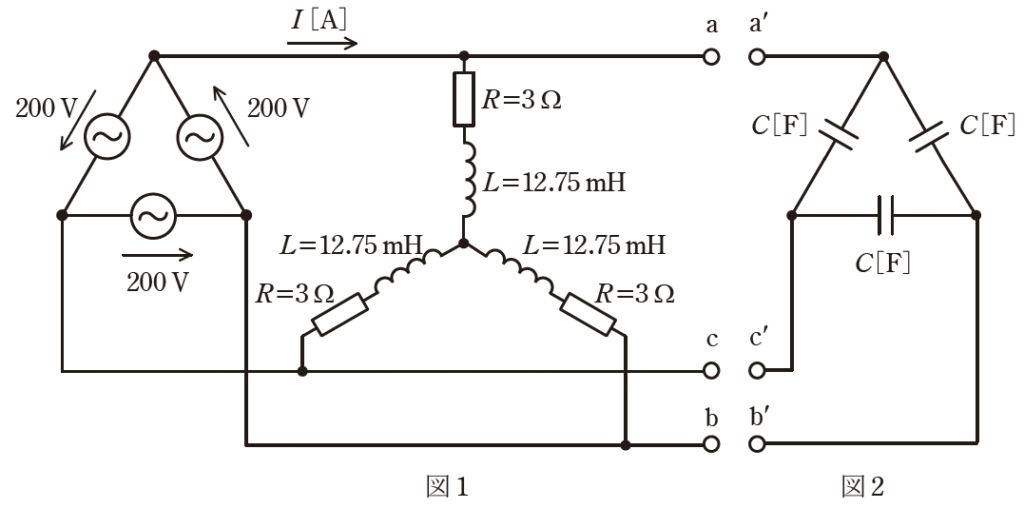
(a) 図1の回路において、負荷電流\(I\)の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)22.2 (2)23.1 (3)40 (4)66.6 (5) 69.2
(b) 図2のように、静電容量\(C[F]\)のコンデンサを結線して、その端子a ,b 及びc をそれぞれ図1 の端子a,b 及びc に接続した。
その結果、三相交流電源から見た負荷の力率は1になったという。
静電容量\(C\) の値\([F]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)\(1.9×10^{-6}\) (2)\(1.7×10^{-4}\) (3)\(2.1×10^{-4}\)
(4)\(7.4×10^{-4}\) (5)\(5.9×10^{-2}\)
答え
(a)(2)
(b)(2)
解説テキスト リンク
回答解説
(a)問題の解答の流れ
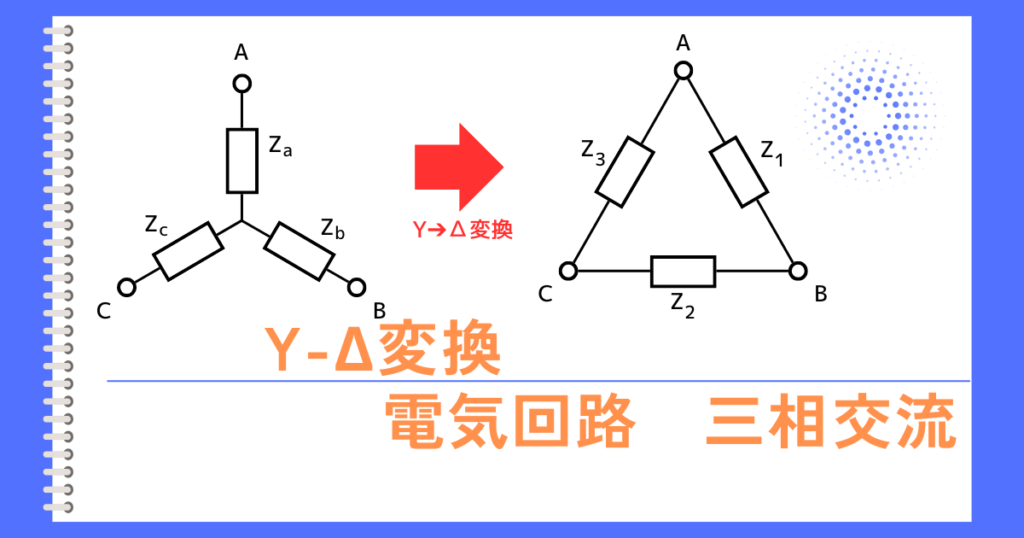
①Y-Δ変換をする
②相電流を求める
③線電流を求める
①Y-Δ変換をする
図1の三相平衡負荷を\(Z_Y\)とすると、
\(Z_Y=R+jωL=R+j2πfL=3+j2π×50×12.75×10^{-3}=3+j4\)
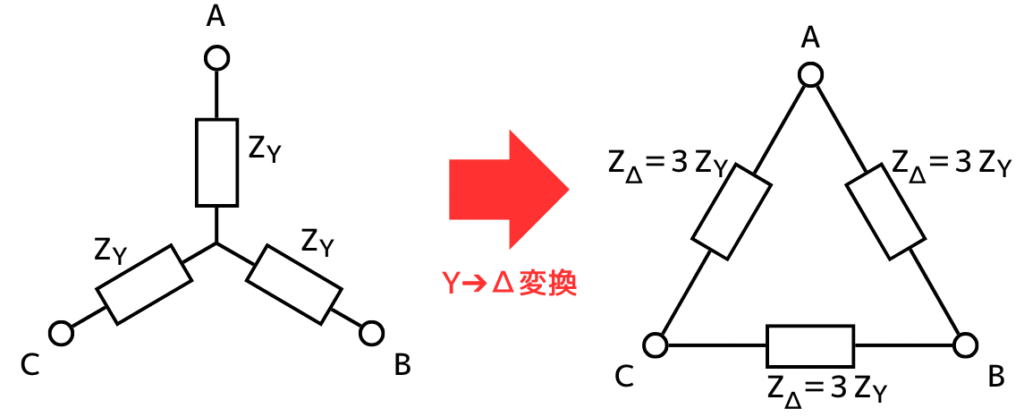
Y-Δ変換すると、抵抗とインダクタンスからなる三相平衡負荷\(Z_Δ\)は、
\(Z_Δ=3Z_Y=9+j12\)
\(|Z_Δ|=\sqrt{9^2+12^2}=15Ω\)
②相電流を求める
Δ結線の各相の相電流を\(I_p\)とすると、
\(\displaystyle I_p=\frac{V}{|Z|}=\frac{200}{15}=13.3A\)
③線電流を求める
線電流\(I\)は相電流\(I_p\)の\(\sqrt{3}\)倍の大きさなので、
\(\displaystyle I=\sqrt{3}I_p=23.1A\)
以上より、(a)問題は(2)23.1 が答えです。
(b)問題の解答の流れ
①負荷条件を整理する
②三相平衡負荷\(Z_Δ\)とコンデンサC[F]の合成インピーダンスを求める
③力率1の条件からコンデンサの静電容量を求める
①負荷条件を整理する
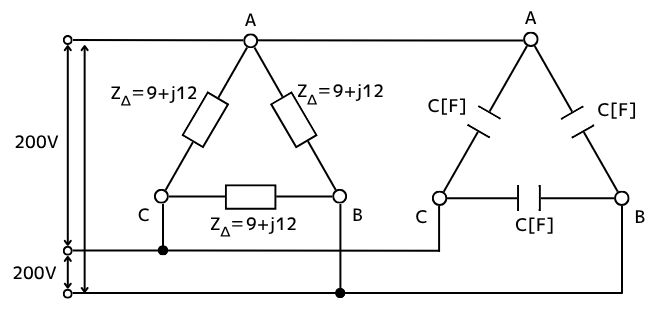
静電容量\(C[F]\)のコンデンサを結線すると、\(Z_Δ\)と、静電容量\(C[F]\)の並列接続になります。
三相平衡負荷の\(Z_Δ\)は、(a)問題から\(Z_Δ=9+j12\) です。
静電容量\(C[F]\)のリアクタンス\(X_C[Ω]\)は、
\(\displaystyle X_C=\frac{1}{j2πfC}\)
②三相平衡負荷\(Z_Δ\)とコンデンサC[F]の合成インピーダンスを求める
(a)問題でY-Δ変換して求めた三相平衡負荷\(Z_Δ\)と、静電容量C[F]のコンデンサは、各相毎に並列接続されたインピーダンスとして扱えますので、その合成インピーダンス\(Z[Ω]\)は、
\(\displaystyle \frac{1}{Z}=\frac{1}{Z_Δ}+\frac{1}{X_C}\)
⇔ \(\displaystyle \frac{1}{Z}=\frac{1}{9+j12}+j2πfC\)
⇔ \(\displaystyle \frac{1}{Z}=\frac{9-j12}{225}+j314C\)
⇔ \(\displaystyle \frac{1}{Z}=\frac{9}{225}-j\frac{12}{225}+j314C\)
③力率1の条件からコンデンサの静電容量を求める
ここで、力率1という条件から、虚数項は0となるので、
\(\displaystyle -j\frac{12}{225}+j314C=0\)
⇔ \(\displaystyle C=\frac{12}{225×314}=1.7×10^{-4}\)
以上より、(b)問題は(2)\(1.7×10^{-4}\) が答えです。
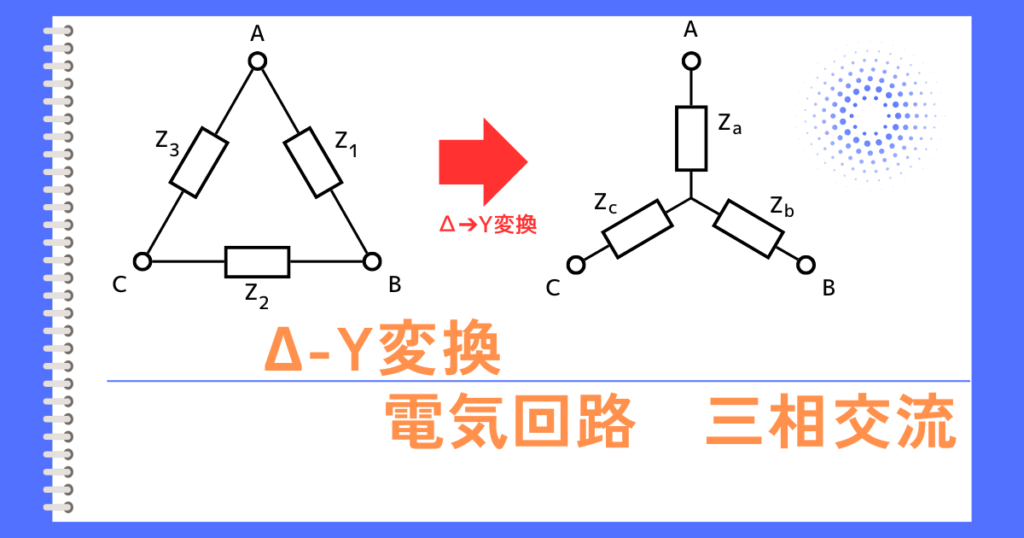
Δ-Y変換の関係式導出
手順
①Δ結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(1)式
②Y結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(2)式
③(1)式=(2)式 から、\(Z_Δ=3Z_Y\)を導出する
①Δ結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(1)式
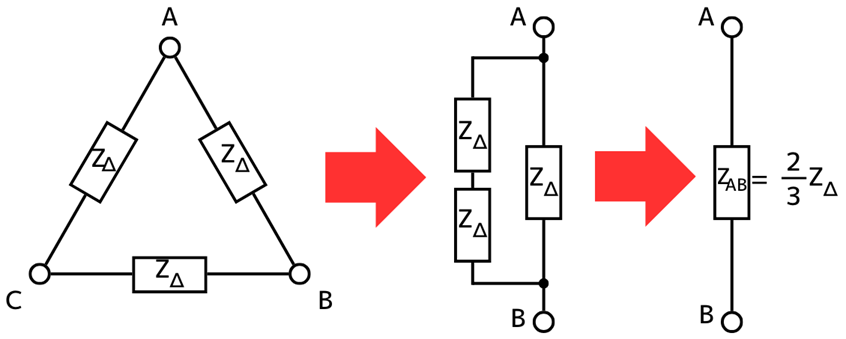
左図から、Δ結線の端子A-B間からみた合成インピーダンス\(Z_{AB}\)は、
\(\displaystyle \frac{1}{Z_{AB}}=\frac{1}{Z_Δ}+\frac{1}{2Z_Δ}\)
整理すると、
\(\displaystyle Z_{AB}=\frac{2}{3}Z_Δ\) …(1)式
②Y結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(2)式
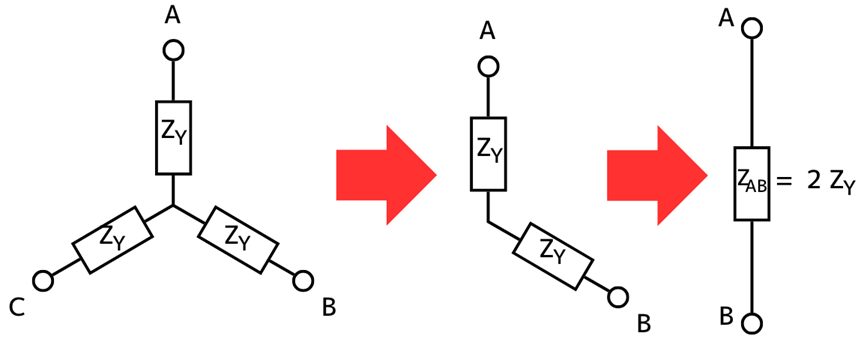
左図から、Y結線の端子A-B間からみた合成インピーダンス\(Z_{AB}\)は、
\(Z_{AB}=2Z_Y\) …(2)式
③(1)式=(2)式 から、\(Z_Δ=3Z_Y\)を導出する
(1)式=(2)式
\(\displaystyle \frac{2}{3}Z_Δ=2Z_Y\)
⇔\(\displaystyle Z_Δ=3Z_Y\)
以上より、\(Z_Δ\)と\(Z_Y\)の関係を求めることが出来ました。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和6年度下期 第三種電気主任技術者試験 理論科目B問題問15
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント