概要
三相交流回路の問題です。難問なので、解答方法に目途が付かない場合は、ある程度で見切りをつける必要があるかと思われます。
(a)問題は、Δ-Y変換が出来ることと、相電圧と線間電圧、相電流と線電流の関係性を理解が必要です。
(b)問題は、次の3点について理解していて正確に計算できないといけないため非常に難しいです。電験二種級の難問だと思われます。
①単相電力計に入力される電圧・電流が何であるか理解すること
②ベクトル図を描いて電圧・電流の位相を把握すること
③複素電力を計算するときは、共役複素数で計算すること
キーワード
三相交流回路、Δ-Y変換、相電圧・線間電圧、相電流・線電流、単相電力計、共役複素数
問題
図のように、線間電圧(実効値)200Vの対称三相交流電源に、1台の単相電力計\(W_1\)、\(X=4Ω\)の誘導性リアクタンス3個、\(R=9Ω\)の抵抗3個を接続した回路がある。
単相電力計\(W_1\)の電流コイルはa相に接続し、電圧コイルはb-c相間に接続され、指示は正の値を示していた。
この回路について、次の(a)及び(b)の問に答えよ。
ただし、対称三相交流電源の相順は、a,b,cとし、単相電力計\(W_1\)の損失は無視できるものとする。
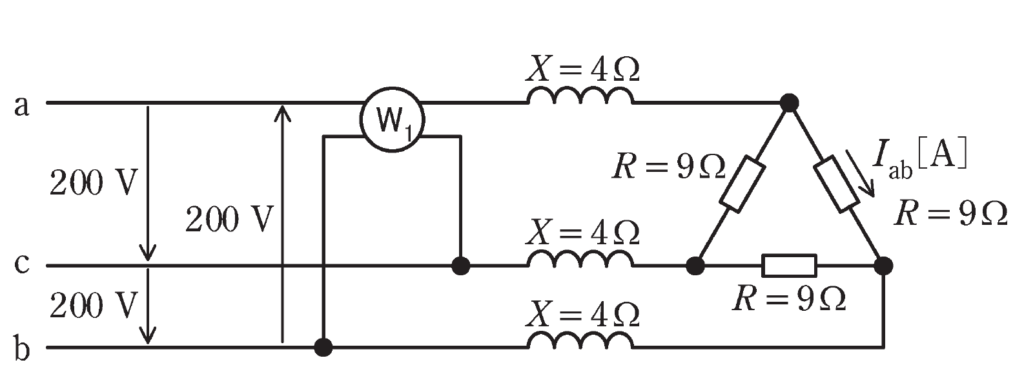
(a)\(R=9Ω\)の抵抗に流れる電流\(I_{ab}\)の実効値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)6.77 (2)13.3 (3)17.3 (4)23.1 (5)40.0
(b)単相電力計\(W_1\)の指示値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)0 (2)2.77 (3)3.70 (4)4.80 (5)6.40
答え
(a)(2)
(b)(3)
解説テキスト リンク
回答解説
(a)の解答の流れ
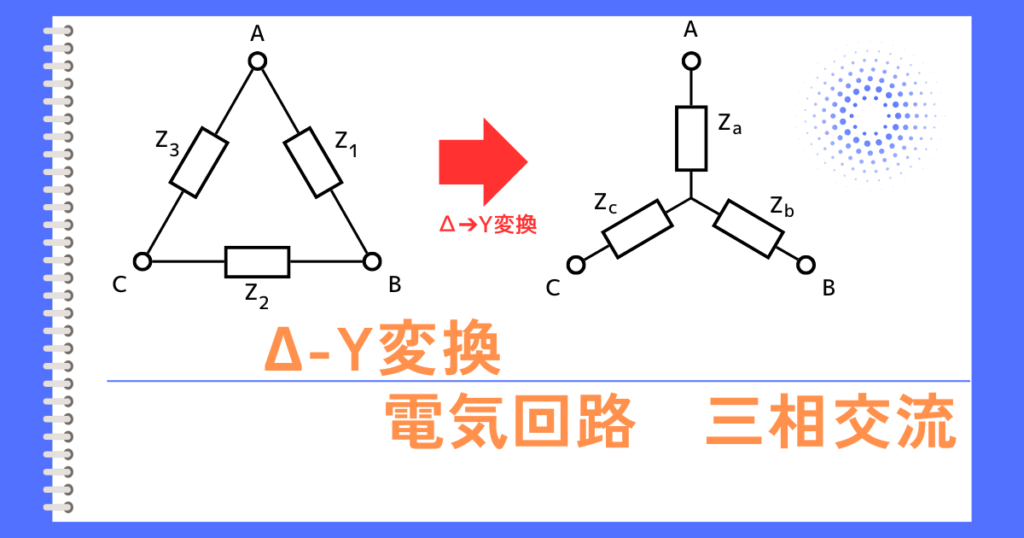
①Δ-Y変換を使い、負荷のΔ結線をY結線に変換する
②線間電圧\(\dot{V_{ab}}\)から相電圧\(\dot{E_a}\)を求める
③1相分の交流回路から線電流\(\dot{I_a}\)を求める
④線電流からΔ結線の相電流\(\dot{I_{ab}}\)を求める
①Δ-Y変換を使い、負荷のΔ結線をY結線に変換する
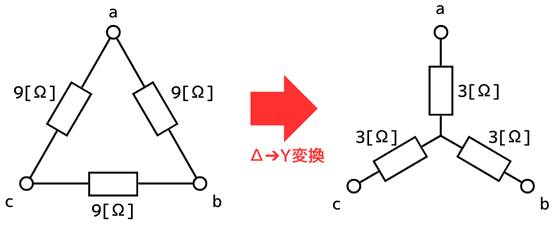
Δ結線の抵抗を\(R_Δ\)、Y結線の抵抗を\(R_Y\)としたとき、Δ-Y変換をすると、次のように計算できます。
\(R_Y=\frac{1}{3}R_Δ=3[Ω]\)
Δ-Y変換を三相交流回路図に反映させると、次の図のように変換できます。
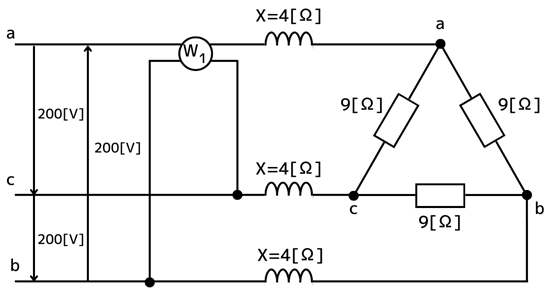
Δ結線
➡
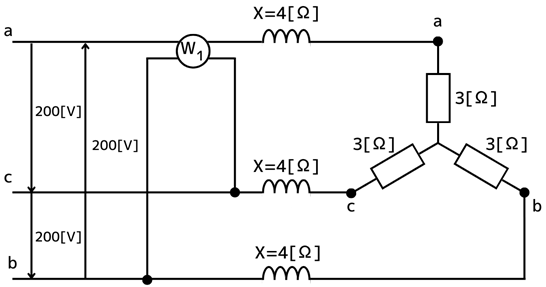
Y結線
②線間電圧\(\dot{V_{ab}}\)から相電圧\(\dot{E_a}\)を求める
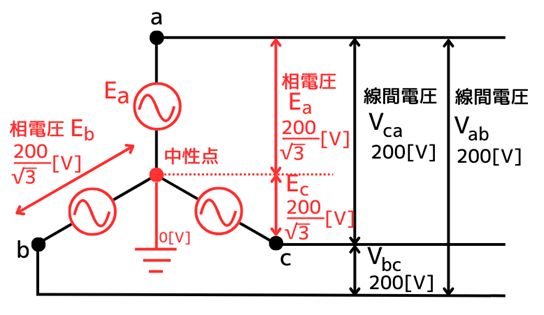
相電圧の大きさ\(\dot{E_a}\)と、線間電圧\(\dot{V_{ab}}\)の関係は、
\(\dot{E_a}=\frac{1}{\sqrt{3}}\dot{V_{ab}}[V]\)
であるため、
\(\dot{E_a}=\frac{200}{\sqrt{3}}[V]\)
③1相分の交流回路から線電流\(I_a\)を求める
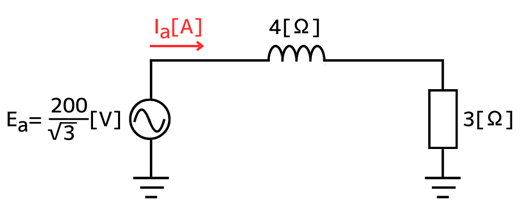
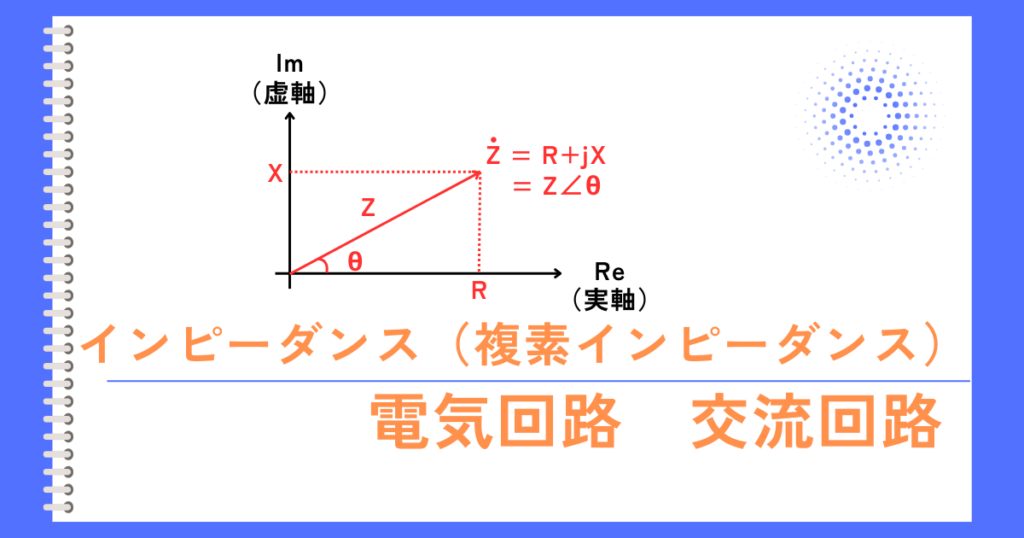
1相分の回路のインピーダンス\(Z[Ω]\)は、
\(\dot{Z}=3+j4\)
なので、
線電流\(\dot{I_a}[A]\)は、
\(\displaystyle \dot{I_a}=\frac{\dot{E_a}}{\dot{Z}}=\frac{\frac{200}{\sqrt{3}}}{3+j4}=\frac{\left( \frac{200}{\sqrt{3}} \right) }{3+j4}・\frac{3-j4}{3-j4}=\frac{200(3-j4)}{25 \sqrt{3}}\)
⇔\(\displaystyle \dot{I_a}=13.86-j18.48\)
④線電流からΔ結線の相電流\(I_{ab}\)を求める
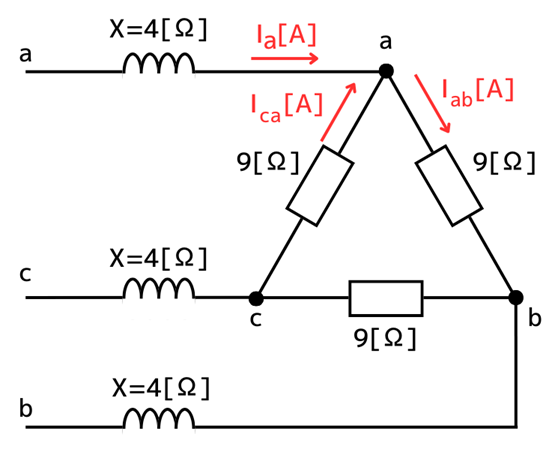
相電流\(\dot{I_{ab}}\)と、線間電流\(\dot{I_a}\)の関係は、
\(\dot{I_{ab}}=\frac{1}{\sqrt{3}}\dot{I_a}[A]\)
であるため、
\(\dot{I_{ab}}=\frac{13.86-j18.48}{\sqrt{3}}=8.0-j10.7[A]\)
相電流\(\dot{I_{ab}}\)の大きさ\(|I_{ab}|\)は、
\(|I_{ab}|=\sqrt{8.0^2+10.7^2}≒13.3A\)
以上より、(2)13.3 が答えとなります。
(b)の解答の流れ
①回路図から、単相電力計\(W_1\)が測定する線間電圧・線電流を読み取る
②問(a)から、線電流\(\dot{I_a}\)を確認する
③線間電圧\(\dot{V_{bc}}\)を求める
④複素電力\(\dot{W_1}=\sqrt{3}\dot{V_{bc}}\bar{\dot{I_a}}\)を求める
①回路図から、単相電力計\(W_1\)が測定する線間電圧・線電流を読み取る
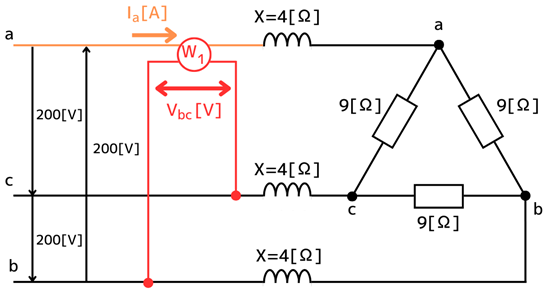
単相電力計\(W_1\)への線間電圧・線電流の入力は、次の通りです。
・線間電圧
電圧コイルがb-c相間に接続されていることから、b-c相の線間電圧が入力されています。
したがって、\(\dot{V_{bc}}\)が入力されていることがわかります。
・線電流
電流コイルがa相に接続されていることから、a相の電流が入力されています。
したがって、\(\dot{I_{a}}\)が入力されていることがわかります。
②問(a)から、線電流\(\dot{I_a}\)を確認する
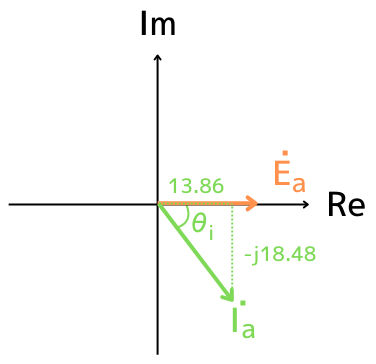
問(a)で、1相分取り出して計算した線電流\(\dot{I_a}\)は、次の通りです。
\(\displaystyle \dot{I_a}=13.86-j18.48\) …②式
相電圧\(\dot{E_a}\)を位相の基準とすると、\(\dot{I_a}\)は\(\dot{E_a}\)よりも\(θ_i[°]\)だけ遅れています。
【蛇足】
試験中は関数電卓が使用できないため計算できませんが、線電流の位相\(I_a\)は\(E_a\)よりも53.1°の遅れです。
\(θ_i=tan^{-1}\frac{13.86}{-18.48}=53.1°\)
③線間電圧\(\dot{V_{bc}}\)を求める
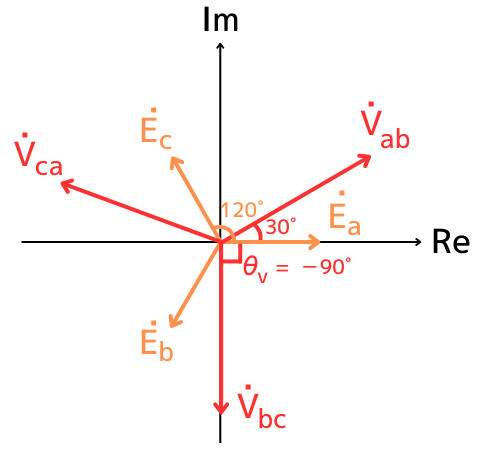
三相交流回路の位相の基準を相電圧\(\dot{E_a}\)としてフェーザ表示で表すと、
\(\dot{E_a}=\frac{200}{\sqrt{3}}∠0°\)
a-b相の線間電圧\(\dot{V_{ab}}\)は、\(\dot{E_a}\)よりも30°進みなので、
\(\dot{V_{ab}}=200∠30°\)
b-c相の線間電圧\(\dot{V_{bc}}\)は、\(V_{ab}\)よりも120°遅れなので、
\(\dot{V_{bc}}=200∠(30°-120°)=200∠-90°\)
線間電圧\(\dot{V_{bc}}\)を複素数で表すと、
\(\dot{V_{bc}}=200(cos(-90°)+jsin(-90°)=200(0-j)=-j200\)
したがって、\(\dot{V_{bc}}=-j200\) …③式
④複素電力\(W_1=\sqrt{3}\dot{V_{bc}}\bar{\dot{I_a}}\)を求める
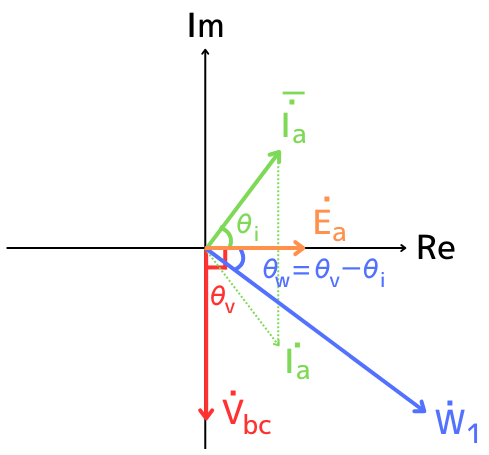
単相電力計\(W_1\)で計測する複素電力は
\(W_1=\dot{V_{bc}}\bar{\dot{I_a}}\)
②式、③式を代入すると、
\(W_1=-j200(13.86-j18.48)\)
⇔\(W_1=-j2772+3696\)
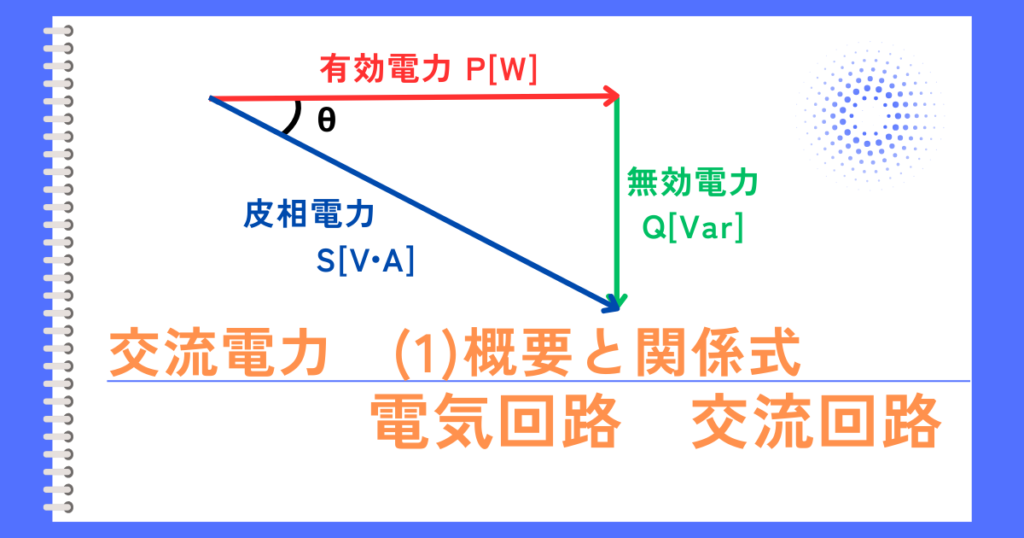
単相電力計は、有効電力を指し示すので、
(3)\(W_1≒3.7kW\)が答えとなります。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和2年度 第三種電気主任技術者試験 理論科目B問題問15
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント