難易度
単相三線式の回路の不平衡負荷における各線の線電流を比較する問題です。
①複素数の計算におけるコイルとコンデンサの扱いについて理解が必要
②キルヒホッフの電流則についての理解が必要
この２点から、難易度は普通程度の問題です。
回路図が少々取っ付き難く感じるかもしれませんが、冷静になって一つ一つ解くルートを探していけば確実に解ける問題です。
この難易度くらいの問題を解けるか否かが合否を分けることでしょう。
問題
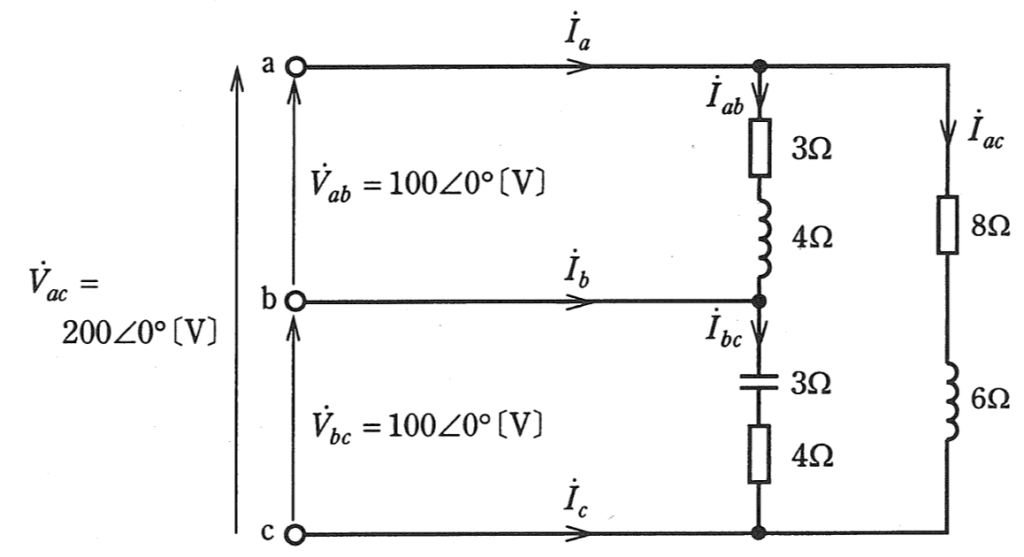
図のように抵抗、コイル、コンデンサからなる負荷がある。
この負荷に線管電圧\(\dot{V}_{ab}=100\angle0°[V]\)、\(\dot{V}_{bc}=100\angle0°[V]\)、\(\dot{V}_{ac}=200\angle0°[V]\)の単相３線式交流電源を接続したところ、端子\(a\)、端子\(b\)、端子\(c\)を流れる線電流はそれぞれ\(\dot{I}_a[A]\)、\(\dot{I}_b[A]\)、\(\dot{I}_c[A]\)であった。
\(\dot{I}_a[A]\)、\(\dot{I}_b[A]\)、\(\dot{I}_c[A]\)の大きさをそれぞれ\(I_a[A]\)、\(I_b[A]\)、\(I_c[A]\)としたとき、これらの大小関係を表す式として、正しいのは次のうちどれか。
(1)\(I_a=I_c>I_b\)
(2)\(I_a>I_c>I_b\)
(3)\(I_b>I_c>I_a\)
(4)\(I_b>I_a>I_c\)
(5)\(I_c>I_a>I_b\)
回答
答え
(2)
回答方針
①各端子間のインピーダンス\(\dot{Z}_{ab}\)、\(\dot{Z}_{bc}\)、\(\dot{Z}_{ca}\)を求めます。
②各端子間の電圧がわかっているので、端子間に流れる電流\(\dot{I}_{ab}\)、\(\dot{I}_{bc}\)、\(\dot{I}_{ac}\)を求めます。
③キルヒホッフの電流則を使用して、各線電流\(\dot{I}_{a}\)、\(\dot{I}_{b}\)、\(\dot{I}_{c}\)を求めて比較します。
要点整理
複素インピーダンスの計算における抵抗・コイル・コンデンサについて
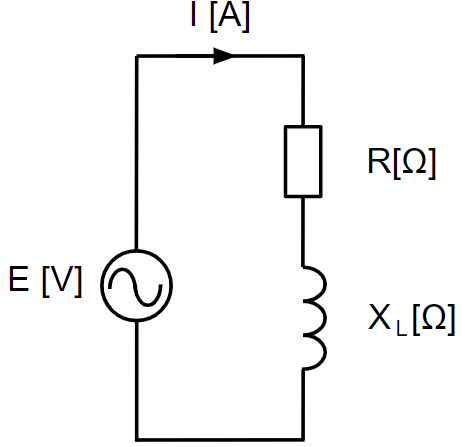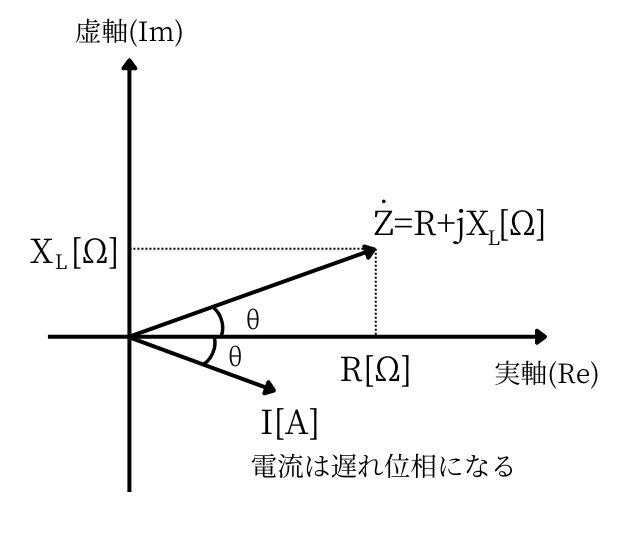  | RL回路の複素インピーダンスの計算について解説します。 \(\dot{Z}_{RL}=R+jX_L [Ω]\) このように表したインピーダンスを複素インピーダンスといいます。 複素インピーダンスの実部\(R\)は抵抗成分を表します。 コイルのリアクタンス成分である虚部\(jX_L\)は、誘導性リアクタンスとも呼びます。 複素インピーダンス\(\dot{Z}_{RL}\)の大きさ\(Z[Ω]\)は、三平方の定理から、 \(Z=\sqrt{R^2+X_L^2}[Ω]\) です。 位相は、\(\displaystyle tan\theta=\frac{Im}{Re}\)なので、 左図のRL回路では、\(\displaystyle tan\theta=\frac{X_L}{R}\)となります。 したがって、位相角は、\(\displaystyle \theta=tan^{-1}\frac{X_L}{R}\) と求まります。 誘導性リアクタンス\(jX_L\)に流れる電流は電圧に対して遅れ位相となります。 そのため、RL回路において、電流は電圧に対して\(\displaystyle \theta=tan^{-1}\frac{X_L}{R}\)だけ遅れ位相となります。 |
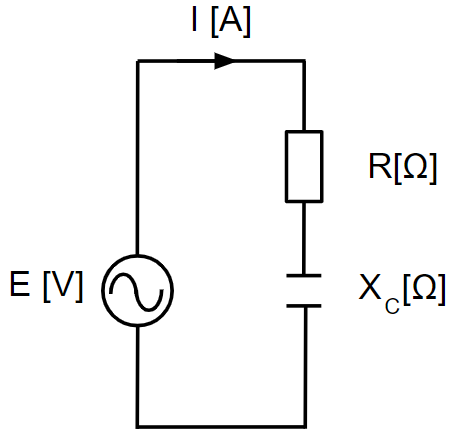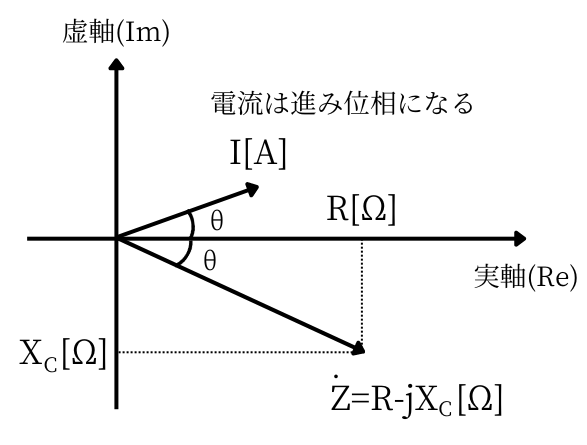  | RC回路の複素インピーダンスの計算について解説します。 コンデンサの場合は、複素インピーダンスは \(\dot{Z}_{RL}=R-jX_C [Ω]\) となり、虚部はマイナスになります。 コンデンサのリアクタンス成分である虚部\(-jX_C\)は、容量性リアクタンスとも呼びます。 複素インピーダンス\(\dot{Z}_{RC}\)の大きさ\(Z[Ω]\)は、三平方の定理から、 \(Z=\sqrt{R^2+X_C^2}[Ω]\) です。 位相は、\(\displaystyle tan\theta=\frac{Im}{Re}\)なので、 左図のRC回路では、\(\displaystyle tan\theta=\frac{-X_C}{R}\)となります。 したがって、位相角は、\(\displaystyle \theta=tan^{-1}\frac{-X_C}{R}\) と求まります。 容量性リアクタンス\(jX_C\)に流れる電流は電圧に対して進み位相となります。 そのため、RC回路において、電流は電圧に対して\(\displaystyle \theta=tan^{-1}\frac{X_C}{R}\)だけ進み位相となります。 |
キルヒホッフの電流則について
キルヒホッフの法則には、
キルヒホッフの電圧則と、キルヒホッフの電流則の２つの法則があります。第一法則、第二法則呼ぶこともあるようです。
本問では、電流則を使用するので、電流則について解説します。
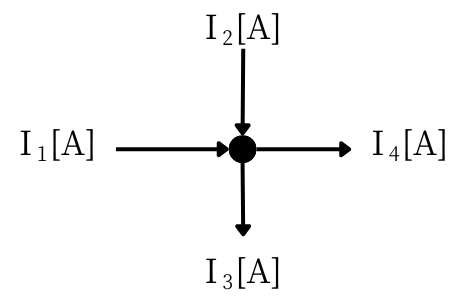 | 左図のような回路中の、分岐点●に入った電流と出ていく電流の和が等しいという法則です。 式にすると、 \(I_1+I_2=I_3+I_4\) となります。 |
要点整理の適用
まず初めに、各端子間のインピーダンス\(\dot{Z}_{ab}\),\(\dot{Z}_{bc}\),\(\dot{Z}_{ca}\)を求めます。
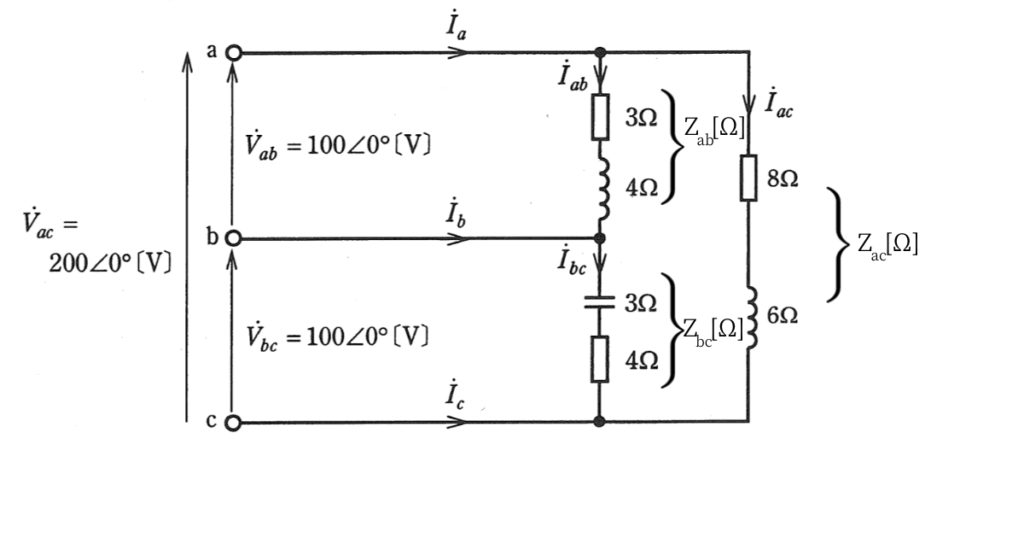
\(\dot{Z}_{ab}=3+j4\) …①
\(\dot{Z}_{bc}=4-j3\) …②
\(\dot{Z}_{ac}=8+j6\) …③
次に、各端子間の電圧がわかっているので、端子間に流れる電流\(\dot{I}_{ab}\),\(\dot{I}_{bc}\),\(\dot{I}_{ac}\)を求めます。
\(\displaystyle
\begin{eqnarray}
\dot{I}_{ab}&=&\frac{\dot{V}_{ab}}{\dot{Z}_{ab}}\\
&=&\frac{100}{3+j4}=\frac{100}{3+j4}・\frac{3-j4}{3-j4}=\frac{100}{3^2+4^2}・(3-j4)\\
&=&12-j16[A]
\end{eqnarray}\)
\(\displaystyle
\begin{eqnarray}
\dot{I}_{bc}&=&\frac{\dot{V}_{bc}}{\dot{Z}_{bc}}\\
&=&\frac{100}{4-j3}=\frac{100}{4-j3}・\frac{4+j3}{4+j3}=\frac{100}{3^2+4^2}・(4+j3)\\
&=&16+j12[A]
\end{eqnarray}\)
\(\displaystyle
\begin{eqnarray}
\dot{I}_{ac}&=&\frac{\dot{V}_{ac}}{\dot{Z}_{ac}}\\
&=&\frac{200}{8+j6}=\frac{200}{8+j6}・\frac{8-j6}{8-j6}=\frac{200}{8^2+6^2}・(8-j6)\\
&=&16-j12[A]
\end{eqnarray}\)
最後に、キルヒホッフの電流則を使用して、各線電流\(\dot{I}_{a}\)、\(\dot{I}_{b}\)、\(\dot{I}_{c}\)を求めて比較します。
\(\dot{I}_{a}=\dot{I}_{ab}+\dot{I}_{ac}=(12-j16)+(16-j12)=28-j28\)
\(\dot{I}_{a}\)の電流の大きさ\(I_{a}\)は、実軸と虚軸の三平方の定理から、
\(I_{a}=\sqrt{28^2+28^2}≒39.6[A]\)
\(\dot{I}_{b}=-\dot{I}_{ab}+\dot{I}_{bc}=-(12-j16)+(16+j12)=4+j28\)
\(\dot{I}_{b}\)の電流の大きさ\(I_{b}\)は、実軸と虚軸の三平方の定理から、
\(I_{b}=\sqrt{4^2+28^2}≒28.3[A]\)
\(\dot{I}_{c}=-\dot{I}_{bc}-\dot{I}_{ac}=-(16+j12)-(16-j12)=-32\)
\(\dot{I}_{c}\)の電流の大きさ\(I_{c}\)は、虚軸がないので、そのまま
\(I_{c}=-32[A]\)
以上より、\(I_{a}>I_{c}>I_{b}\)となりますので、(2)が答えです。
出典元
平成２１年度第三種電気主任技術者試験 理論科目Ａ問題問７
参考書
本ブログの管理人は、電験３種過去問マスタを使って３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント