概要
RC回路の過渡応答の問題です。
コンデンサに蓄えられた電荷を放電している最中の過渡状態を解析して時定数を求める問題と、静電エネルギーから消費エネルギーを求める問題の二本立てです。
2種類の問題を問われてはいるものの、それぞれの問題は簡単な問題です。
キーワード
RC回路、過渡応答、時定数、静電エネルギー
問題
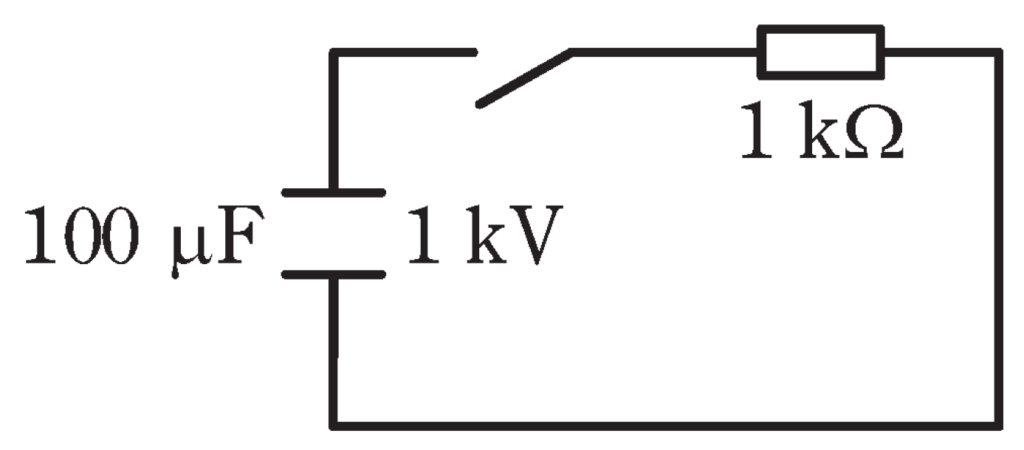
図のように、電圧\(1kV\)に充電された静電容量\(100μF\)のコンデンサ、抵抗\(1kΩ\)、スイッチからなる回路がある。
スイッチを閉じた直後に過渡的に流れる電流の時定数\(τ\)の値\([s]\)と、スイッチを閉じてから十分に時間が経過するまでに抵抗で消費されるエネルギー\(W\)の値\([J]\)の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| \(τ\) | \(W\) | |
| (1) | 0.1 | 0.1 |
| (2) | 0.1 | 50 |
| (3) | 0.1 | 1000 |
| (4) | 10 | 0.1 |
| (5) | 10 | 50 |
答え
(2)
解説テキスト リンク
回答解説
回答の流れ
(a)過渡解析をする
①RC回路の\(v(t)\)について微分方程式を立てる
②過渡状態を解析して時定数を導出する
(b)消費エネルギーを計算する
③スイッチを閉じる前の静電エネルギーを求める
④スイッチを閉じた後の静電エネルギーを求める
⑤スイッチを閉じる前後の静電エネルギーの差から、抵抗で消費されたエネルギーを求める

(a)過渡解析をする
①RC回路の\(v(t)\)について微分方程式を立てる
回路中を流れる電流を\(i[A]\)とします。
電流の定義式から、次の電流\(i\)と電荷\(q\)の関係式が出せます。
\(\displaystyle i=\frac{dq}{dt}\)
コンデンサの電荷、静電容量、電圧の関係式から
\(q=cv\)
電流と電荷の関係式に代入すると、
\(\displaystyle i=C \frac{dv}{dt}\)
回路の方程式は、次式となります。
\(0=Ri+v\)
⇔ \(\displaystyle 0=CR\frac{dv}{dt}+v\)
②過渡状態を解析して時定数を導出する
コンデンサ電圧の過渡解を\(v_t\)とします。
\(v_t=ke^{-st}\)
としたとき、\(v_t\)を微分すると、
\(\displaystyle \frac{dv_t}{dt}=-ske^{-st}\)
過渡解を求める方程式は、
\(0=ke^{-st}-CRske^{-st}=(1-CRs)ke^{-st}\)
上式が成り立つ条件は、
\(\displaystyle s=\frac{1}{CR}\)
です。
時定数\(τ\)は、過渡解の式中の\(e^{-st}\)が\(e^{-1}\)となるときの時間であるため、
\(\displaystyle τ=\frac{1}{s}=CR=100×10^{-6}・10^3=0.1[s]\)
したがって、時定数\(τ=0.1s\)と求まりました。
(b)消費エネルギーを計算する
③スイッチを閉じる前の静電エネルギーを求める
スイッチを閉じる前のコンデンサに蓄えられている静電エネルギー\(W_1[J]\)は、
\(\displaystyle W_1=\frac{1}{2}CV^2=\frac{1}{2}×100×10^{-6}×(10^3)^2=50J\)
④スイッチを閉じた後の静電エネルギーを求める
スイッチを閉じて十分時間が経った後は、コンデンサの電圧\(v=0V\)となるため、コンデンサに蓄えられている静電エネルギー\(W_2[J]\)は、
\(\displaystyle W_2=0J\)
⑤スイッチを閉じる前後の静電エネルギーの差から、抵抗で消費されたエネルギーを求める
スイッチを閉じた後、コンデンサに蓄えられていた静電エネルギーは、全て抵抗で消費されます。
そのため、スイッチを閉じる前後の静電エネルギーの差を求めることで、抵抗で消費されるエネルギー\(W\)を求めることができます。
\(W=W_1-W_2=50-0=50J\)
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和1年度 第三種電気主任技術者試験 理論科目A問題問10
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント