難易度
磁気に関する基礎知識問題です。
ひねりは特にないので、確実に回答したい問題です。
問題
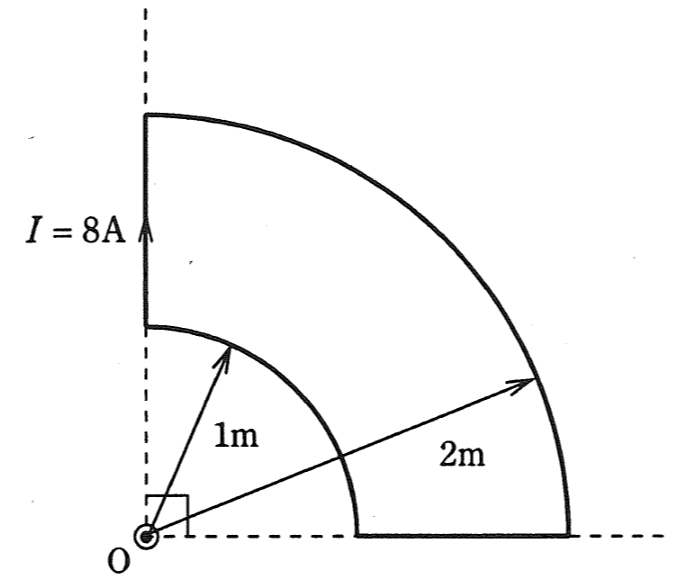
図のように、点(O)を中心とするそれぞれ半径\(1[m]\)と半径\(2[m]\)の円形同線の
\(\displaystyle \frac{1}{4}\)と、それらを連結する直線状の導線からなる扇形導線がある。
この導線に、図に示す向きに直流電流\(I=8[A]\)を流した場合、点\(O\)における磁界\([A/m]\)の
大きさとして、正しいのは次のうちどれか。
ただし、扇形導線は同一平面状にあり、その巻数は一巻きである。
(1)0.25 (2)0.5 (3)0.75 (4)1.0 (5)2.0
回答
答え
(2)
回答方針
電流が作る磁界について基本的な式を理解していること。
扇形導線は、向きごとに４つの導体に分けて考えること。
各導体が作る磁界の大きさを合成できること。
この３つが出来れば、回答できます。
それぞれ難しいことではないので、着実に理解していければ間違えることはないでしょう。
要点整理
電流が作る磁界についての基本的な式について整理します。
電流と磁界の関係を考える際のアプローチは２つあります。
１つ目は、アンペアの法則です。
２つ目は、ビオ・サバールの法則です。
それぞれについてアプローチしていきます。
アンペアの法則
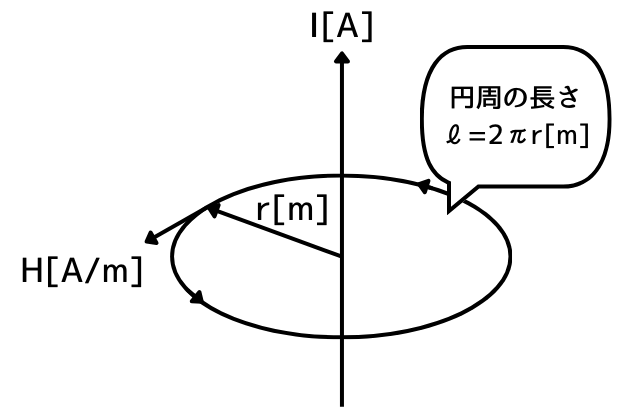
電流が作る磁界中で、磁界の強さが等しい所をたどって１周したときの磁路の長さ\(l=2\pi r[m]\)と、磁界の強さ\(H[A/m]\)の積が、電流\(I[A]\)に等しいという法則です。
式に示すと、
\( \displaystyle I=\oint_C Hdl\) \(=Hl=H\times 2\pi r \)
となります。変形すると、
\(\displaystyle H=\frac{I}{2\pi r}[A/m]\)
となります。
ビオ・サバールの法則（直線電流の作る磁界）
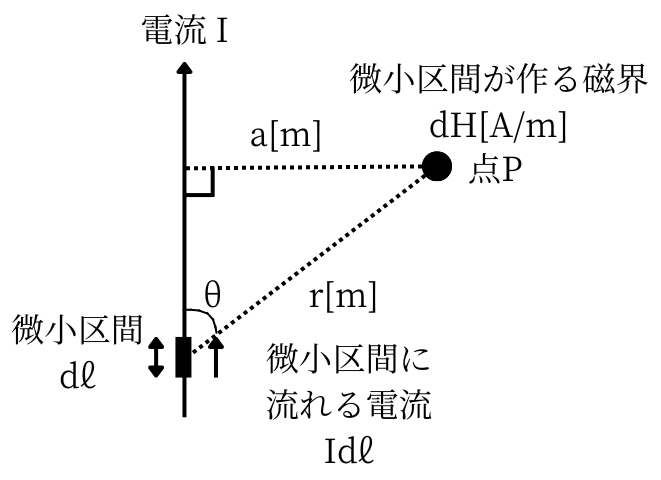
微小な電流要素から得られる微小な磁界の強さを積分することで、電流と磁界の関係を導き出します。静電界について磁界について学ぶ際、式の対応が取れている事を足掛かりとして学ぶことが多いでしょう。
上図のように、直線電流\(I[A]\)が流れている電線から、\(a[m]\)離れた距離にある点\(P\)の磁界を求めます。
\(微小区間dl\)に流れる電流は、\(Idl\)です。
なす角を\(\theta\)、微小区間\(dl\)からの距離を\(r[m]\)としたとき、微小区間が点\(P\)に作る磁界\(dH[A/m]\)は、
\(\displaystyle dH=\frac{Idl}{4\pi r^2}・sin\theta\)
となります。
静電界における電束密度の式は、\(\displaystyle D=\frac{Q}{4\pi r^2}\)ですので、非常に似通った式であることがわかります。
磁界の式の分母の\(\displaystyle 4\pi r^2\)は、球の表面積です。
分子の\(\displaystyle Idl・sin\theta\)が、静電界における\(Q\)に対応していることがわかります。
ここで、\(sin\theta\)が何故出てくるのかという疑問が浮かぶと思います。
\(sin\theta\)出てくる理由は、微小電流ベクトル\(I\overrightarrow{dl}\)と、位置ベクトル\(\vec{r}\)の外積によって磁界ベクトルが出来るため、\(sin\theta\)が出てきます。
式をベクトル形式で書くと、
\(\displaystyle \overrightarrow{dH}=\frac{I}{4\pi}\frac{\overrightarrow{dl}}{r^2}\times\frac{\vec{r}}{r}\)
となります。
それを、スカラー形式に書き換えて簡素化すると、
\(\displaystyle dH=\frac{I}{4\pi}\frac{|dl||r|sin\theta}{r^3}=\frac{Idl}{4\pi r^2}sin\theta\)
となります。
微小区間が作る磁界\(dH\)が求まったので、次は全区間が作る磁界\(H\)を求めていきます。
 |  |
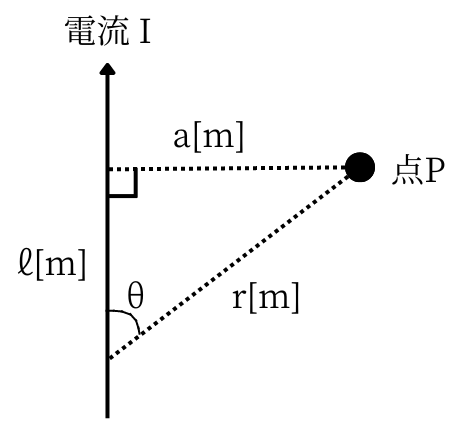微小区間\(dl\)を積分することで、電線に流れる電流\(I\)が、点\(P\)に作る磁界\(H\)を求めることが出来ます。
\(\displaystyle H= \int_{-\infty}^{\infty} \frac{Isin\theta}{4\pi r^2}dl\)
\(\displaystyle \frac{I}{4\pi}\)は、定数であるため、積分の外に出します。
すると、変数は\(\displaystyle \frac{sin\theta}{r^2}\)となります。書き換えると、
\(\displaystyle H=\frac{I}{4\pi}\int_{-\infty}^{\infty} \frac{sin\theta}{r^2}dl\)…①
このままだと計算できないので、\(dl\)の積分ではなく、\(d\theta\)の積分に変換することを考えます。
\(a=r sin\theta\)から、\(\displaystyle r=\frac{a}{sin\theta}\)…②
\(\displaystyle l=-r cos\theta=-\frac{a cos\theta}{sin\theta}\)…③
\(l\)は、原点よりマイナス側に居るので、マイナスを付けています。
③を\(d\theta\)で微分
\(\displaystyle \frac{dl}{d\theta}=-\left(\frac{-a sin\theta sin\theta -a cos\theta cos\theta}{sin^2\theta}\right)=\frac{a}{sin^2}\)
よって、\(\displaystyle dl=\frac{a}{sin^2}d\theta\)…④
積分範囲は
\(-\infty→0\)、\(\infty→\pi\)…⑤
①に②④⑤を代入すると、
\(H\) \(\displaystyle =\frac{I}{4\pi}\int_0^{\pi} \frac{sin\theta}{a}d\theta=\frac{1}{4\pi a}\left[-cos\theta\right]_0^\pi=\) \(\displaystyle \frac{1}{2\pi a}[A/m]\)
と求まります。
ビオ・サバールの法則（円形コイルの作る磁界）
今回の問題は一巻の円形コイルの中心に生じる磁界の求め方が必要となるため、ビオ・サバールの法則から求めます。
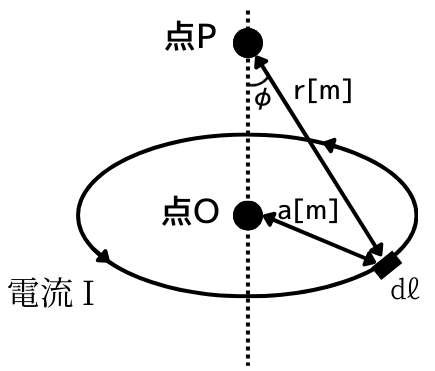
次は、円形コイルに電流が流れた場合の、コイルの中心を点O、中心軸上の任意の点を点Pとしたときの、点Oの磁界を求めます。
点Oの磁界を求めるには、点Pのなす角\(φ\)が\(90°\)の時に点Oとなるので、まずは任意の点Pの磁界について考えます。
\(\displaystyle dH=\frac{Idl}{4\pi r^2}・sin\theta\)…①
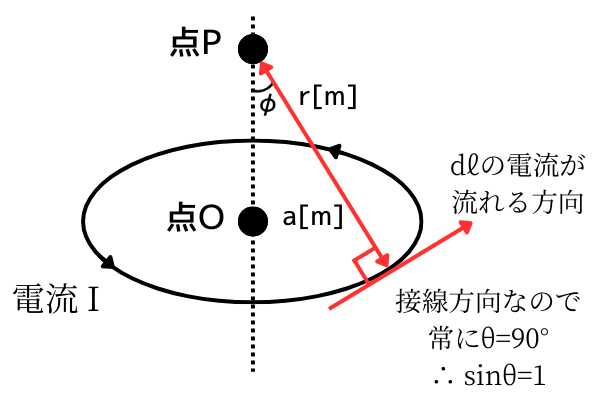
微小区間dlの電流が流れる方向と、点Pのなす角が、\(sin\theta\)です。
円形コイルに電流が流れているため、dlの電流が流れる方向はコイルの接線方向です。dlの方向と、点Pのなす角は常に\(\theta=90°\)であるため、\(sin\theta=1\)です。
したがって、①式は、
\(\displaystyle dH=\frac{Idl}{4\pi r^2}\)…②
となります。
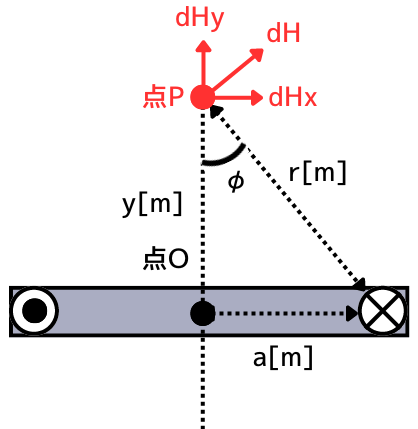
コイルを横から見たとき、\(dl\)が作る磁界は\(dH\)、\(dH_x\)、\(dH_y\)と分解できます。
コイルは、点Pの周りを１周するため、\(dH_x\)のベクトル和は\(0\)になります。
したがって、
\(dH_y=dH sinφ\)…③
となります。③に②を代入すると、
\(\displaystyle dH_y=\frac{Idl}{4\pi r^2}・sinφ\)…④
となります。④式を積分すると、
\(\displaystyle H_y=\int_0^{2\pi a}\frac{I}{4\pi r^2}・sinφ dl\)…⑤
となります。\(dl\)の位置が動くことによって、変化する変数は、⑤式には存在しないので、
\(\displaystyle H_y=\frac{I}{4\pi r^2}・sinφ\int_0^{2\pi a} dl\)…⑥
と、書き換える事ができます。積分の計算をすると、
\(\displaystyle H_y=\frac{I}{4\pi r^2}・sinφ・2\pi a\)…⑦
となります。
\(\displaystyle sinφ=\frac{a}{r}\)…⑧
なので、⑦に⑧を代入すると、
\(\displaystyle H_y=\frac{Ia^2}{2 r^3}\)…⑨
となります。
\(r=\sqrt{a^2+y^2}\)…⑩
なので、⑩を⑨に代入すると、
\(\displaystyle H_y=\frac{Ia^2}{2 (a^2+y^2)^{\frac{3}{2}}}\)…⑪
以上より、任意の点Pにおける磁界の強さ
\(\displaystyle H_y=\frac{Ia^2}{2 (a^2+y^2)^{\frac{3}{2}}}\)が求まりました。
点Oにおける磁界の強さは、\(y=0\)の時を考えれば良いので、
\(\displaystyle H_y=\frac{I}{2a}\)
となります。
要点整理の適用
問題の扇形導線を、向きごとに４つの辺として考えます。
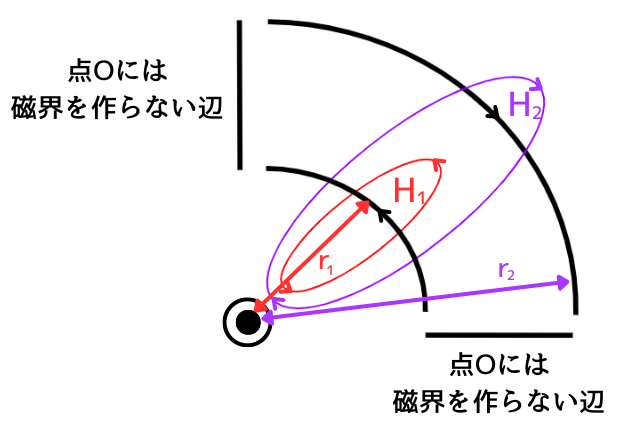
内側の辺は\(H_1\)、外側の辺は\(H_2\)の磁界を作るとします。
この時、要点整理で解説したビオ・サバールの法則のうち、一巻の円形コイルの中心に生じる磁界の考え方を使います。
それぞれの辺は円形同線の\(\displaystyle \frac{1}{4}\)なので、点Oにできる磁界は、
\(\displaystyle H_1=\frac{1}{4}・\frac{I}{2r_1}=\frac{1}{4}・\frac{8}{2}=1[A/m]\)
\(\displaystyle H_2=\frac{1}{4}・\frac{I}{2r_2}=\frac{1}{4}・\frac{8}{4}=0.5[A/m]\)
磁界の大きさを合成すると、\(H_1\)と\(H_2\)の向きは逆なので、
\(H=H_1-H_2=0.5[A/m]\)
となります。
出典元
平成２１年度第三種電気主任技術者試験 理論科目Ａ問題問４
参考書
本ブログの管理人は、電験３種過去問マスタを使って電験３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント