概要
2つの電源を持つ回路の問題です。
直流回路の問題の中でも、比較的簡単な問題です。
重ねの理や、キルヒホッフの法則を使った方程式を立てる等のいくつかの解法があります。
キーワード
重ねの理、キルヒホッフの法則、消費電力の計算
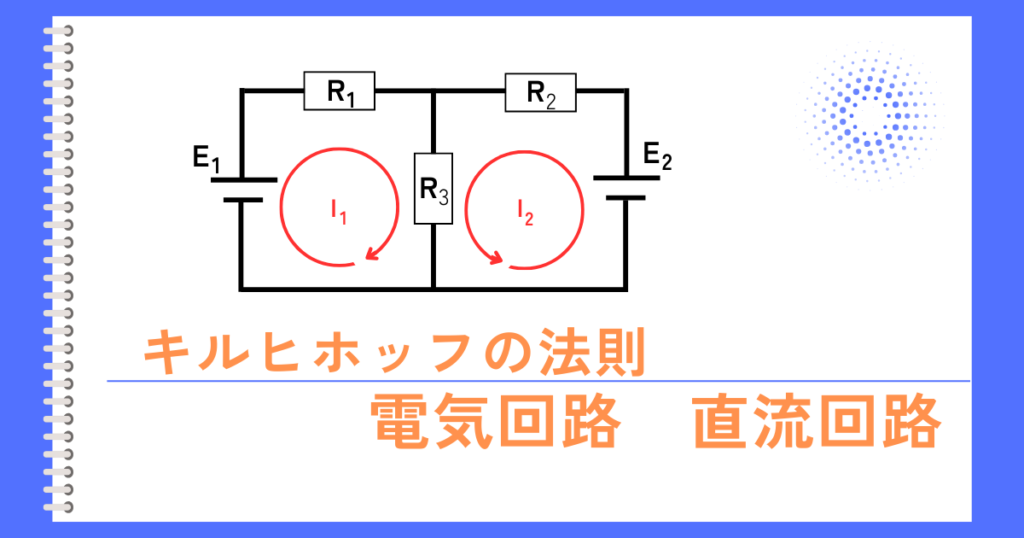
問題
図の直流回路において、抵抗\(R = 10Ω\) で消費される電力の値[W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
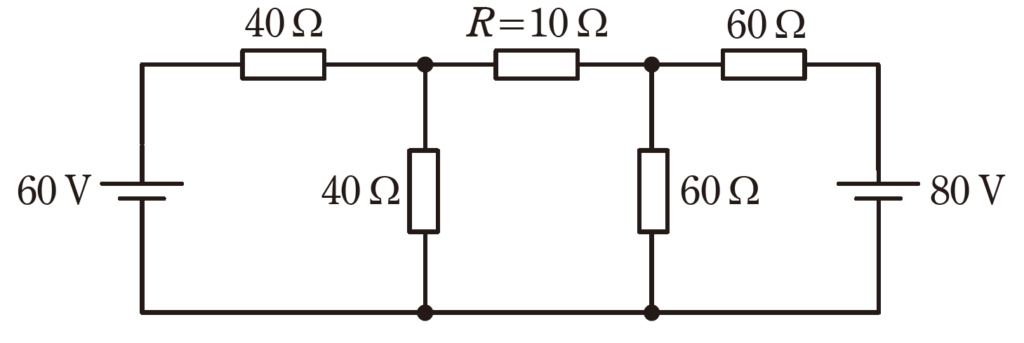
(1) 0.28 (2) 1.89 (3) 3.79 (4) 5.36 (5) 7.62
答え
(1)
関連解説 テキストページ
回答解説
重ねの理で解く
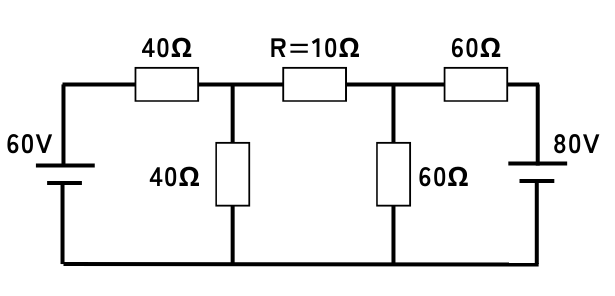
① 60Vの電圧源の解析
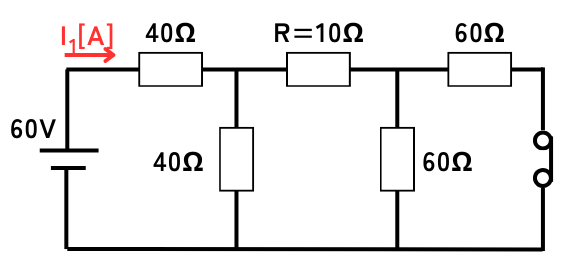
60V側の電圧源について、回路解析をします。
もう片方の電圧源(80V)は、短絡除去します。
60Vの電圧源から回路に送られる電流は、\(I_1[A]\)とします。
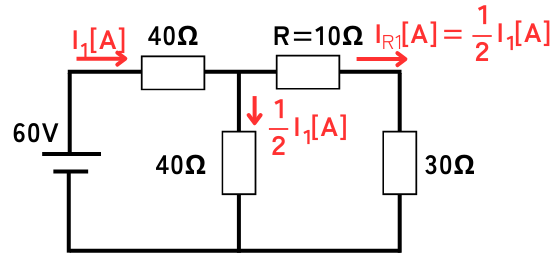
回路を少し簡略化します。
\(R=10Ω\)に流れる電流は、
\(\displaystyle I_{R1}=\frac{40}{40+10+30}I_1=\frac{1}{2}I_1[A]\)です。
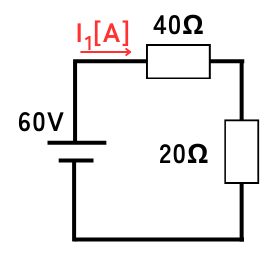
\(I_1[A]\)を導出するために更に簡略化します。
\(\displaystyle I_1=\frac{V}{R}=\frac{60}{40+20}=1[A]\)
したがって、\(I_{R1}=\frac{1}{2}I_1=0.5[A]\)
② 80Vの電圧源の解析
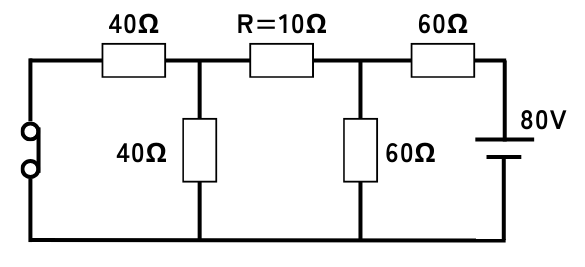
80V側の電圧源について、回路解析をします。
もう片方の電圧源(60V)は、短絡除去します。
80Vの電圧源から回路に送られる電流は、\(I_2[A]\)とします。
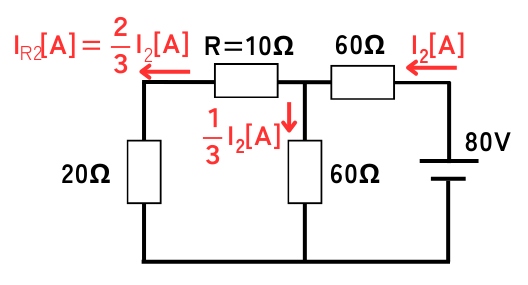
回路を少し簡略化します。
\(R=10Ω\)に流れる電流は、
\(\displaystyle I_{R2}=\frac{60}{60+10+20}I_2=\frac{2}{3}I_2[A]\)です。
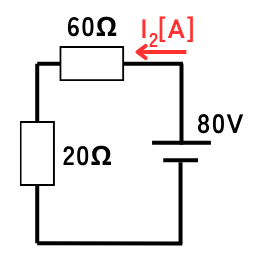
\(I_2[A]\)を導出するために更に簡略化します。
\(\displaystyle I_2=\frac{V}{R}=\frac{80}{60+20}=1[A]\)
したがって、\(I_{R2}=\frac{2}{3}I_2=0.667[A]\)
③ 結果の重ね合わせ
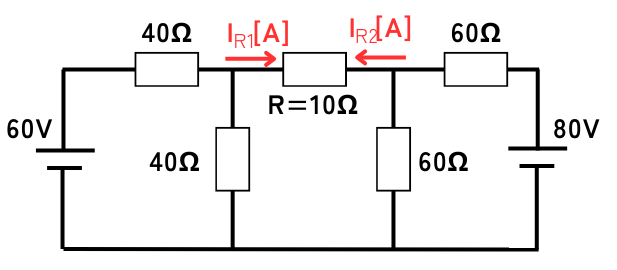
①・②で解析した結果\(I_{R1}\)、\(I_{R2}\)を重ね合わせます。電流が左から右側に流れる方向をプラスとして計算すると、
\(I_R=I_{R1}-I_{R2}=0.5-0.667=-0.167[A]\)
となるので、電流が右から左に流れています。
電流と、抵抗値がわかったので、抵抗Rの消費電力は、
\(P=I^2R=0.167^2 ・10≒0.28[W]\)
以上より、(1) 0.28 が答えです。
キルヒホッフの法則で解く
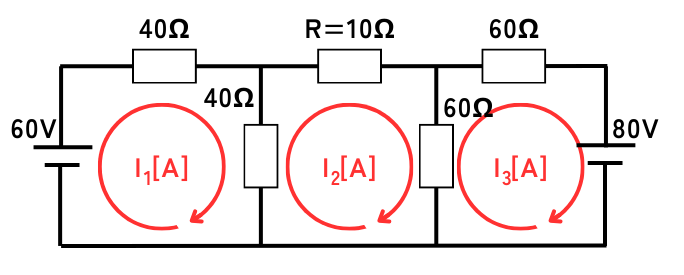
キルヒホッフの法則から、方程式を立式します。
\(\displaystyle \begin{eqnarray}
\left\{
\begin{array}{l}
60&=&40I_1+40(I_1-I_2) \\
0&=&40(I_2-I_1)+10I_2+60(I_2-I_3)\\
-80&=&60(I_3-I_2)+60I_3
\end{array}
\right.
\end{eqnarray}\)
整理すると、
\(\displaystyle \begin{eqnarray}
\left\{
\begin{array}{l}
60&=&80I_1-40I_2+0 …① \\
0&=&-40I_1+110I_2-60I_3 …②\\
-80&=&0-60I_2+120I_3 …③
\end{array}
\right.
\end{eqnarray}\)
①式から、\(I_1=0.75+0.5I_2\) …④
③式から、\(I_3=-0.667+0.5I_2\) …⑤
②式に④・⑤式を代入すると、
\(-40(0.75+0.5I_2)+110I_2-60(-0.667+0.5I_2)=0\)
⇔\(10+60I_2=0\)
⇔\(I_2=-0.1667\) …⑥
⑥式から、時計回りに流れるとした\(I_2\)はマイナスなので、右側から左側に電流が流れることがわかる。
電流と、抵抗値がわかったので、抵抗Rの消費電力は、
\(P=I^2R=0.167^2 ・10≒0.28[W]\)
以上より、(1) 0.28 が答えです。
出典元
令和5年度上期 第三種電気主任技術者試験 理論科目A問題問5
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント