難易度
点電荷と平行平板コンデンサに関する基礎知識問題です。
ひねりは特にないので、確実に回答したい問題です。
問題
静電界に関する記述として、正しいのは次のうちどれか。
（1）二つの小さな帯電体の間に働く力の大きさは、それぞれの帯電体の電気量の和に比例し、その距離の２乗に反比例する。
（2）点電荷が作る電界は点電荷の電気量に比例し、距離に反比例する。
（3）電気力線上の任意の点での接線の方向は、その点の電界の方向に一致する。
（4）等電位面上の正電荷には、その面に沿った方向に正のクーロン力が働く。
（5）コンデンサの電極板間にすき間なく誘電体を入れると、静電容量と電極板間の電界は、誘電体の誘電率に比例して増大する。
回答
答え
(3)
回答方針
点電荷と、電気力線に関する理解が重要な問題です。
イメージとして覚えることが重要です。
要点整理
電荷に関連する要点整理をします。
- 電荷\(Q [C] \)
- 誘電率\(ε[F/m]\)
比誘電率\(ε_r\)、真空の誘電率\(ε_0[F/m]\)とすると、
\(ε=ε_rε_0\)の関係式があります。 - 電機力線の本数\(N[本]\)
\(\displaystyle N=\frac{Q}{ε}[本]\) - 電界の強さ\(E[V/m]\)
電界の強さ\(E[V/m]\)は、電気力線密度であるので、
\(\displaystyle E=\frac{N}{S}=\frac{Q}{εS}\)となります。
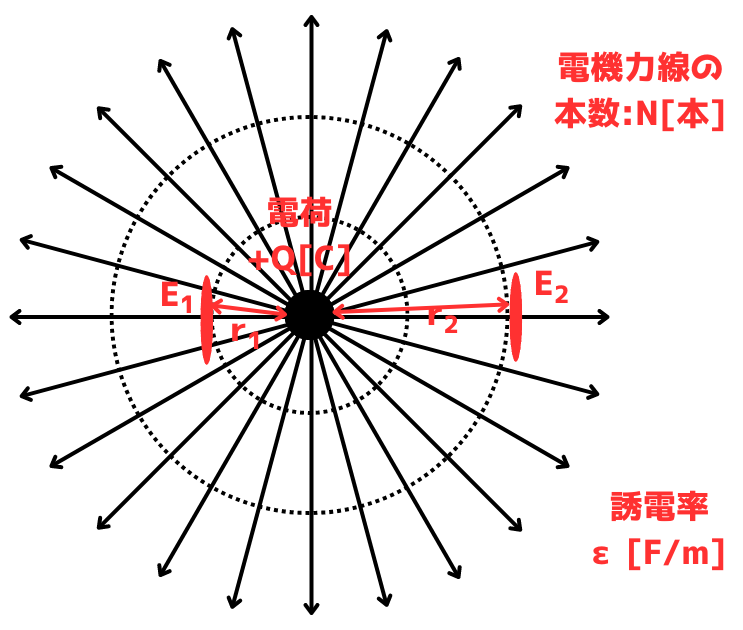 | 半径\(r_1 [m] \)の時の球の面積を\(S_1 [m^2] \)、電界の強さを\(E_1[V/m]\)とします。 半径\(r_2 [m] \)の時の球の面積を\(S_2 [m^2] \)、電界の強さを\(E_2[V/m]\)とします。 半径\(r_1\)よりも半径\(r_2\)の方が大きいとします。 電界の強さ\(E\)は電気力線密度であるので、赤い輪に入る電気力線の本数が多ければ、\(E\)は大きくなります。 左図から、半径が小さい\(r_1\)の時は、\(E_1\)には電気力線が3本通っており、半径が大きい\(r_2\)の時は、１本通っています。 このことから、半径\(r\)が大きくなると、球の面積\(S\)が大きくなり、電界の強さ\(E\)が弱くなることがわかります。 |
電界の強さと距離の関係を求める際、分母にある面積\(S\)は、状況に応じて全く異なるので、３つのパターンに分けて要点整理します。
①点電荷の場合
電界の強さは、半径\(r [m] \)の球の表面積は\(S=4 \pi r^2[m^2] \)なので、電界の強さは\(\displaystyle E=\frac{Q}{4\pi εr^2}[V/m]\)となります。
②ケーブルの場合
電界の強さは、半径\(r [m] \)のケーブルの表面積は\(S=2 \pi r[m^2] \)なので、電界の強さは\(\displaystyle E=\frac{Q}{2\pi εr}[V/m]\)となります。
③平行平板コンデンサの場合
電界の強さは、極板間距離を\(d [m] \)、極板面積を\(S[m^2] \)とすると、極板面積は常に一定の\(S[m^2] \)なので、電界の強さは\(\displaystyle E=\frac{Q}{ε S}[V/m]\)となります。
- 電界の向き
電気力線の接線方向が電界の向きです。 - クーロン力\(F [N] \)
電界の強さ\(E[V/m]\)の電界の中に、\(q [C] \)の電荷を置いたとき、\(q [C] \)の電荷に働くクーロン力\(F [N] \)は、\(F=qE [N] \)となります。
電界の強さの式を代入すると、\(F=\frac{qQ}{4\pi εr^2} [N] \)となります。
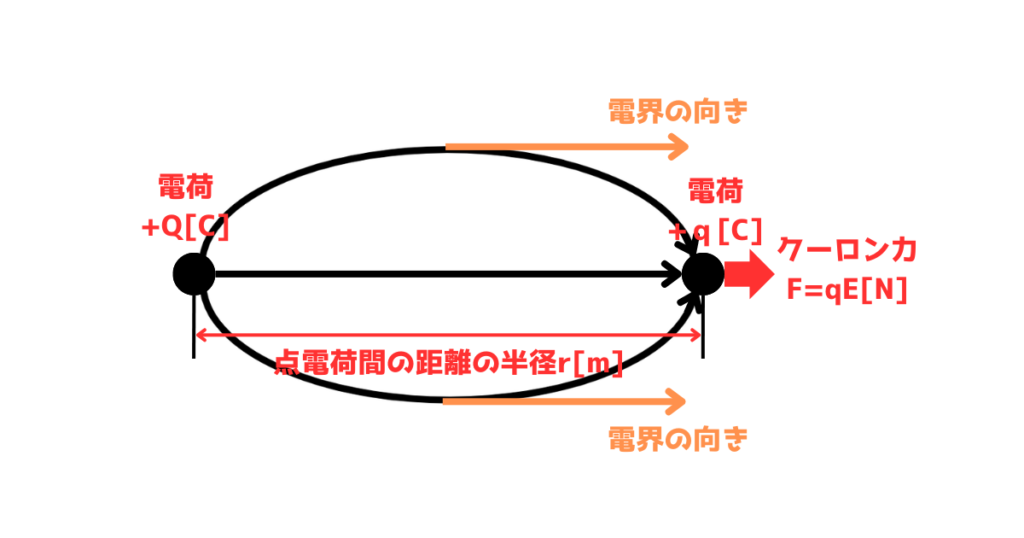 | 電荷\(+Q[C]\)が作り出す電界の強さ\(E[V/m]\)は、距離が離れれば離れる程弱くなります。 そのため、クーロン力\(F=qE [N] \)は小さくなります。 |
要点整理の適用
要点整理で書き出した内容を、各回答に適用します。
（1）二つの小さな帯電体の間に働く力の大きさは、それぞれの帯電体の電気量の和に比例し、その距離の２乗に反比例する。
二つの小さな帯電体の間に働く力はクーロン力です。
クーロン力の式は、\(\displaystyle F=qE [N]=\frac{qQ}{4\pi εr^2} \)であることから、二つの帯電体の電荷qと、Qの積に比例することがわかります。
したがって、帯電体の電気量の和は間違っています。
（2）点電荷が作る電界は点電荷の電気量に比例し、距離に反比例する。
電界の強さ\(\displaystyle E=\frac{Q}{4\pi εr^2}[V/m]\)の式から、電界は点電荷の電気量に比例します。
しかし、距離の２乗に反比例しますので、この選択肢は間違っています。
（3）電気力線上の任意の点での接線の方向は、その点の電界の方向に一致する。
電気力線の接線方向が電界の向きですので、正解です。
（4）等電位面上の正電荷には、その面に沿った方向に正のクーロン力が働く。
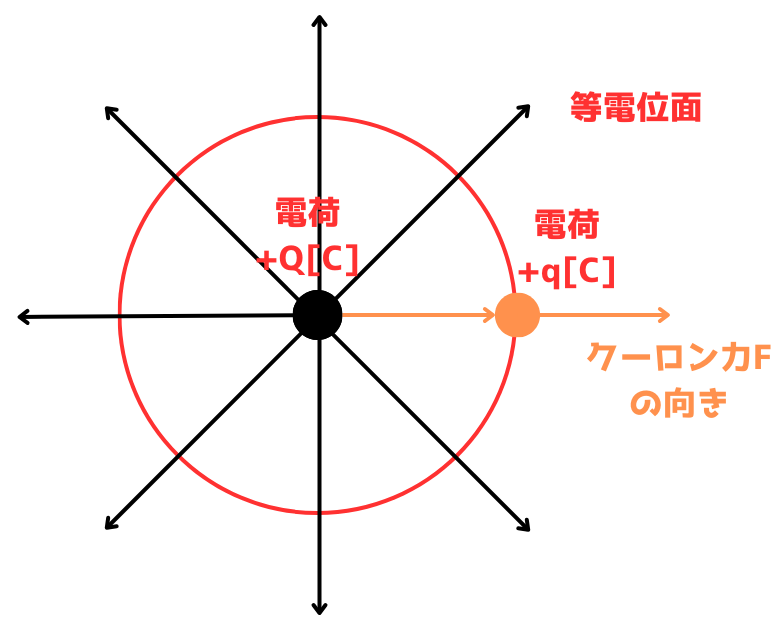 | 左図の赤い円は、電荷+Qが作り出す等電位面です。 等電位面上に、+qの電荷を置いた時、左図の通り、等電位面に対して垂直の向きに正のクーロン力が働いていることがわかります。 したがって、この選択肢は間違っています。 |
（5）コンデンサの電極板間にすき間なく誘電体を入れると、静電容量と電極板間の電界は、誘電体の誘電率に比例して増大する。
平行平板コンデンサの場合の電界の強さの式から、\(\displaystyle E=\frac{Q}{ε S}[V/m]\)となります。
したがって、誘電体の誘電率に反比例しますので、選択肢は間違っています。
また、静電容量は\(Q=CV \)の関係から、\(C=\frac{Q}{V} \)となります。
詳細は省きますが、\(V=Ed \)の関係があるため、\(C=ε\frac{S}{d} \)となります。
したがって、静電容量は誘電体の誘電率に比例して増大しますので、静電容量に関しては合っています。
出典元
平成２１年度第三種電気主任技術者試験 理論科目Ａ問題問２
参考書
本ブログの管理人は、電験３種過去問マスタを使って電験３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント