公式一覧
ローレンツ力のベクトル式
\(\vec{F}=q(\vec{E}+\vec{v}×\vec{B})\)
ローレンツ力のベクトル式(第2項のみ)
\(\vec{F}=q\vec{v}×\vec{B}\)
ローレンツ力の向きと大きさ
\(F=qvBsinθ[N]\)
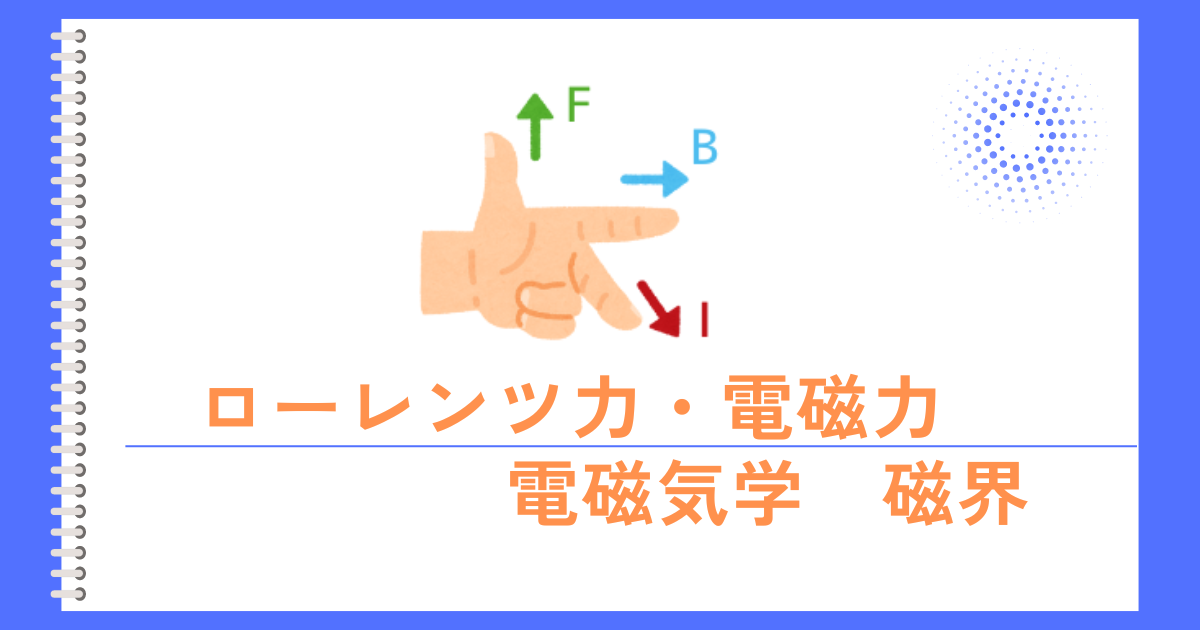
フレミング左手の法則の親指の向き
ローレンツ力による起電力の式
\(V=vBlsinθ[V]\)
フレミング右手の法則の中指の向き
電磁力のベクトル式
\(\vec{F}=\vec{I}×\vec{B}l\)
電磁力の向きと大きさ
\(F=IBlsinθ[N]\)
フレミング左手の法則の親指の向き
ローレンツ力・電磁力の違い
ローレンツ力、電磁力について触れる前に、この2つの力について違いを説明します。
ローレンツ力は、自由電子等の荷電粒子が電磁界から受ける力です。
電磁力は、導体を流れる電流が磁界から受ける力です。
自由電子の移動が電流であることから、各電子に働くローレンツ力が集まった力が電磁力です。
つまり、ローレンツ力はミクロな視点で見た時の力であり、電磁力はマクロな視点で見た時の力です。
例えば、電磁界中で導線に電流が流れている時、導線中を流れる電子一つ一つに働く力はローレンツ力、電流によって導線に働く力は電磁力です。
ローレンツ力
ローレンツ力のベクトル式
\(\vec{F}=q(\vec{E}+\vec{v}×\vec{B})\)
ローレンツ力のベクトル式(第2項のみ)
\(\vec{F}=q\vec{v}×\vec{B}\)
ローレンツ力の大きさと向き
フレミング左手の法則の親指の向きに、\(F=qvBsinθ[N]\)の大きさのローレンツ力が発生します。
ローレンツ力のベクトル式について
電磁界中で、荷電粒子が受ける電磁気的な力をローレンツ力と呼び、ローレンツ力のベクトル式は、\(\vec{F}=q(\vec{E}+\vec{v}×\vec{B})\)で表されます。
ローレンツ力のベクトル式の第1項 \(q\vec{E}\) はクーロン力であり、荷電粒子が電界から受ける力です。第2項 \(q\vec{v}×\vec{B}\) は荷電粒子が磁界から受ける力です
電界強度\(\vec{E}\)の電界と、磁束密度\(\vec{B}\)の磁界を合わせた力場を電磁界と呼びます。
電磁界ではなく、磁界のみ与えられている場合のローレンツ力は第2項のみを使います。
ローレンツ力の大きさ
電験三種の問題でローレンツ力の問題を解くときは、ベクトル\(\vec{F}\)のまま計算するのは難しいので、ローレンツ力の向きと、大きさを別々に分解して計算していきます。
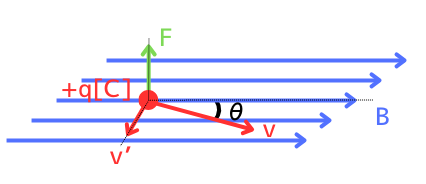
磁束密度\(\vec{B}[T]\)の磁界中を、\(q[C]\)の電荷が速度\(\vec{v}[m/s]\)で動くと、ローレンツ力\(\vec{F}[N]\)を受けます。
これを、ローレンツ力を式に表すと、
\(\vec{F}=q\vec{v}×\vec{B}\)
です。
\(\vec{v}×\vec{B}\)は、電荷の移動速度\(v\)と磁束密度\(B\)の外積を表しますので、\(\vec{v}×\vec{B}\)の大きさは、\(vBsinθ\)です。
従って、ローレンツ力\(F\)の大きさは、
\(F=qvBsinθ\)
となります。
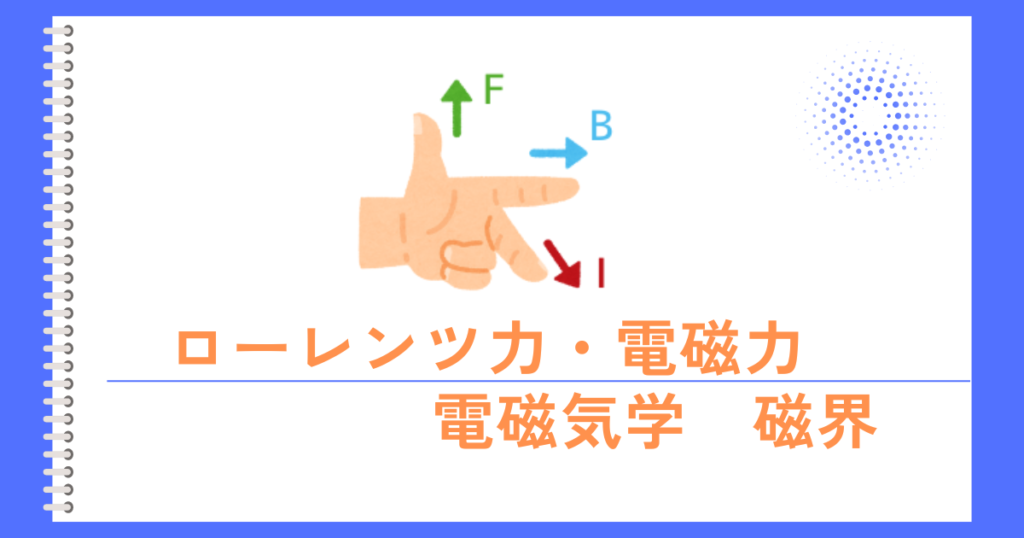
ローレンツ力の向き(フレミング左手の法則)
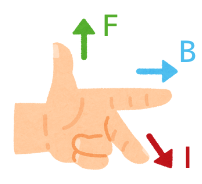
左手を左図のように構えた時
親 指:力(\(F[N]\))の向き
人差し指:磁界(\(B[T]\))の向き
中 指:電流(\(I[A]\))の向き
ローレンツ力による起電力
ローレンツ力による起電力の式
\(V=vBlsinθ[V]\)
磁束密度\(\vec{B}[T]\)の磁界中で、導体を速度\(\vec{v}[m/s]\)で移動させたときに、導体中の自由電子にローレンツ力\(\vec{F}[N]\)が働くことで起電力\(V[V]\)が発生します。
ローレンツ力による起電力の原理
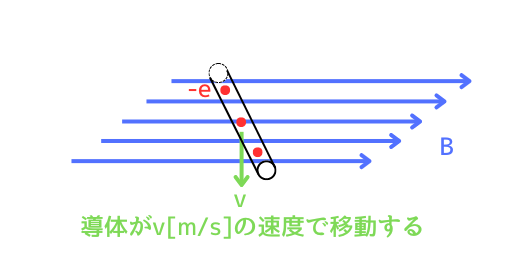
①磁界中の導体を移動
磁束密度\(B[T]\)の磁界中に置かれた導体を
速度\(v[m/s]\)で動かすと、導体内に存在する自由電子も一緒に速度\(v[m/s]\)で動きますので、\(v\)の方向に、電流が流れていると考えることができます。
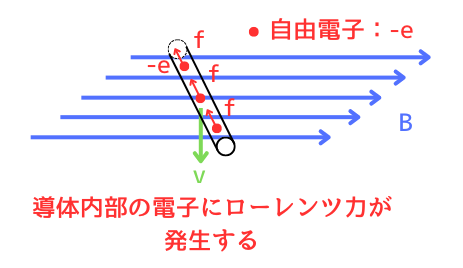
②ローレンツ力による電子の移動
磁界中を自由電子が移動すると、ローレンツ力\(F_L[N]\)が発生します。
ローレンツ力の大きさは、導体の移動の向きと、磁界の向きのなす角をθとしたとき、
\(F_L=-evBsinθ\)
です。
電子は負電荷なので、ローレンツ力の発生する向きは、フレミング左手の法則の中指を速度\(v\)の向きにしたときに親指が向く向きと逆方向です。
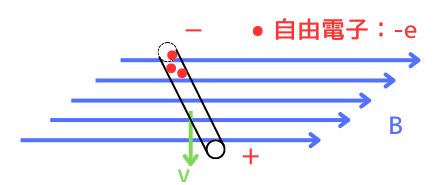
③電子の偏りによる帯電
電子が移動して減った側は、電子が不足するので正(+)に帯電します。電子が集まった側は、負(-)に帯電します。
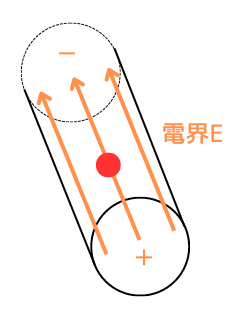
④電界の発生
正に帯電した+側と、負に帯電した-側の間に、電界の強さ\(E[V/m]\)の静電界が発生します。
静電界が作り出すクーロン力\(F_C\)と、磁界内の移動によって発生するローレンツ力\(F_L\)が釣り合うまで、電子は-側に移動します。
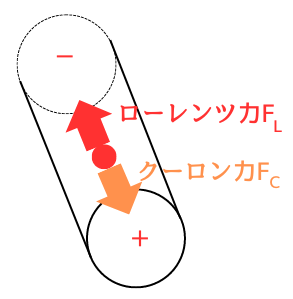
⑤起電力の発生
クーロン力の大きさは、\(F_C=-eE\) …①
ローレンツ力の大きさは、\(F_L=-evBsinθ\) …②
ですので、①=②より、
\(F_C=F_L\)
⇔ \(-eE=-evBsinθ\)
⇔ \(E=vBsinθ\) …③
これで、電界の強さ\(E[V/m]\)が求まりました。
平行平板コンデンサのように考えると、電位\(V[V]\)と電界の強さ\(E\)の関係は、
\(V=Ed\) ⇔ \(\displaystyle E=\frac{V}{d}\) …④
です。
\(d[m]\)は、ここでは導体の長さ\(l[m]\)であるので、\(d=l\)とします。
③式に④式を代入すると、
\(\frac{V}{l}=vBsinθ\)
⇔\(V=vBlsinθ\)

起電力\(V[V]\)の向きは、左図の通りとなります。
ローレンツ力による起電力の向き(フレミング右手の法則)
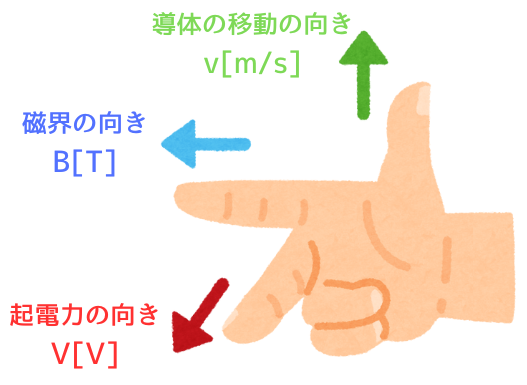
右手を左図のように構えた時
親 指:移動(\(v[m/s]\))の向き
人差し指:磁界(\(B[T]\))の向き
中 指:起電力(\(V[V]\))の向き
電磁力
電磁力のベクトル式
\(\vec{F}=\vec{I}×\vec{B}l\)
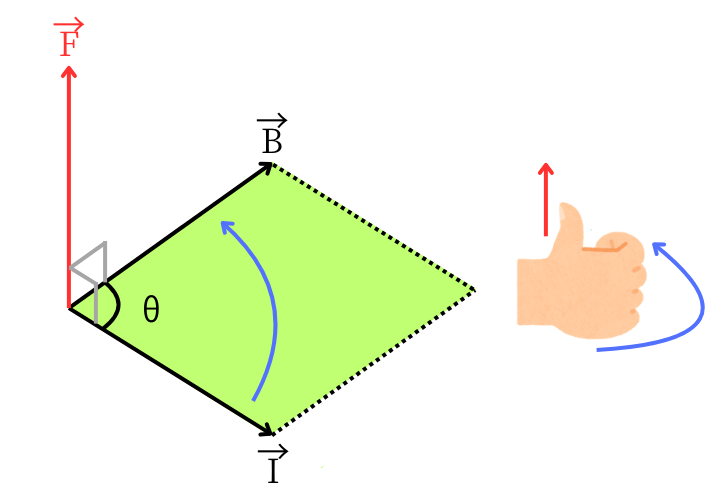
電磁力の向きと大きさ
フレミング左手の法則の親指の向きに、\(F=IBlsinθ[N]\)の大きさの電磁力が発生します。
電磁界中で電流が受ける電磁気的な力を電磁力と呼びます。
電磁力\(\vec{F}\)、電流\(\vec{I}\)、磁束密度\(\vec{B}\)は、それぞれ方向と大きさを持つベクトルであるため、次式で表されます。
電磁力の大きさ
電磁力の式について解説します。
電磁力\(\vec{F}[N]\)は、電流\(\vec{I}[A]\)と、磁束密度\(\vec{B}[T]\)の外積で表されます。これを式で表すと、
\(\vec{F}=\vec{I}\times\vec{B}\)
となります。ベクトルの式に出てくる \(×\) の記号は、外積を表します。
電磁力の向きは、電流の向きから磁界の向きに右ねじの法則で回したときに、親指が向く向きです。
\(\vec{F}\)の大きさは、\(\vec{I}\)と\(\vec{B}\)の作る平行四辺形の面積と同じです。つまり、
\(|F|=|I| |B| sinθ\)
です。導体の長さを\(l[m]\)とすると
\(F=IBlsinθ\)
と求まります。
電磁力の向き

ローレンツ力と同じくフレミング左手の法則で電磁力の向きが示されます。
左手を左図のように構えたとき、次のように向きを示します。
親 指:力(\(F[N]\))の向き
人差し指:磁界(\(B[T]\))の向き
中 指:電流(\(I[A]\))の向き
ローレンツ力から電磁力の導出
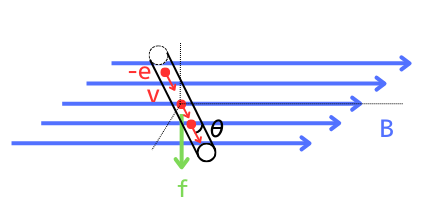
①流れる電子に発生するローレンツ力
電流は、負電荷である電子\(-e[C]\)が流れているので、1個の電子に発生するローレンツ力は、
\(f=-evBsinθ[N]\) …①
電子は負電荷なので、電子にかかるローレンツ力の向きは、フレミング左手の法則の親指の向きと逆方向です。
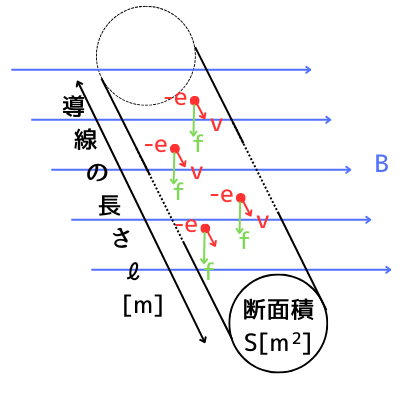
②電子の個数\(N\)[個]
導線の中に存在する自由電子の個数\(N\)[個]は、
・自由電子数の密度\(n[個/m^3]\)
・断面積\(S[m^2]\)
・長さ\(l[m]\)
としたとき、次式で表されます。
\(N=nSl[個]\) …②
③導線に発生する電磁力(ローレンツ力の総和)
導線に存在する\(N\)[個]の電子に発生するローレンツ力の総和は
\(F=f[N]・N[個]\) …③
です。
③式に、①・②式を代入すると、次式となります。
\(F=-evBsinθ・nSl=-envSBlsinθ\) …④
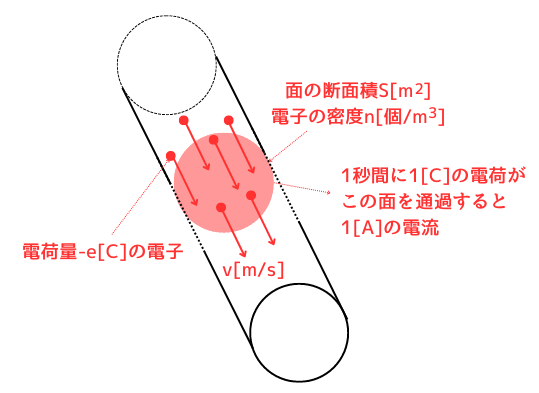
④電子と電流
1秒間に1[C]の電荷が流れるとき、1[A]の電流となります。導線に、次の条件の電子が流れているとき、
・電荷量\(-e[C]\)
・電子の密度\(n[個/m^3]\)
・電子の速度\(v[m/s]\)
・導線の面積\(S[m^2]\)
電流の大きさは、\(I=-envS[A]\) …⑤
となります。
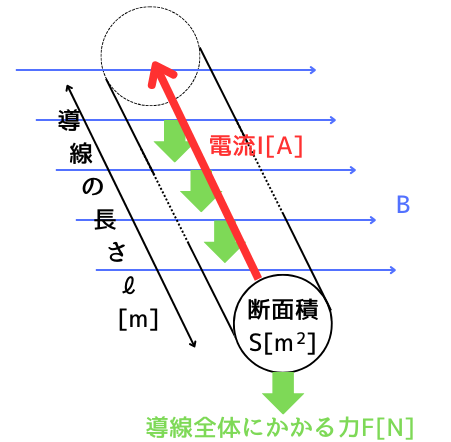
⑤式を④式に代入すると、
\(F=IBlsinθ[N]\)
と、求まりました。
関連事項
ローレンツ力や、電磁力を考える際に関連する事項をまとめます。
偶力について
偶力とは、次の3条件が揃った力です。
①大きさが等しい
②向きが正反対
③平行(同じ直線上にない)2つの力
偶力は、合力をもとめられないので1対の力として扱います。
偶力が1つの物体に働くと、物体は回転します。
偶力と、偶力ではない力の例を図に示します。

偶力となる2つの力の例です
①大きさが等しく
②向きが正反対で
③平行(同じ直線上にない)



偶力でない力の例です
①大きさが等しくない
②向きが正反対でない
③平行でない
偶力を使った物の例
ネジは、ドライバーを使って回転させるとき、手で偶力を発生させて回しています。
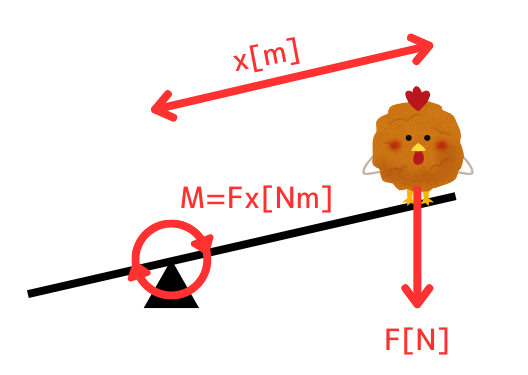
モーメントについて
モーメントとは、支点にかかる物体を回転させる力のことです。
モーメント\(M[Nm]\)は、かかる力\(F[N]\)と、支点からの距離\(x[m]\)の積で表します。
\(M=Fx[Nm]\)
外積
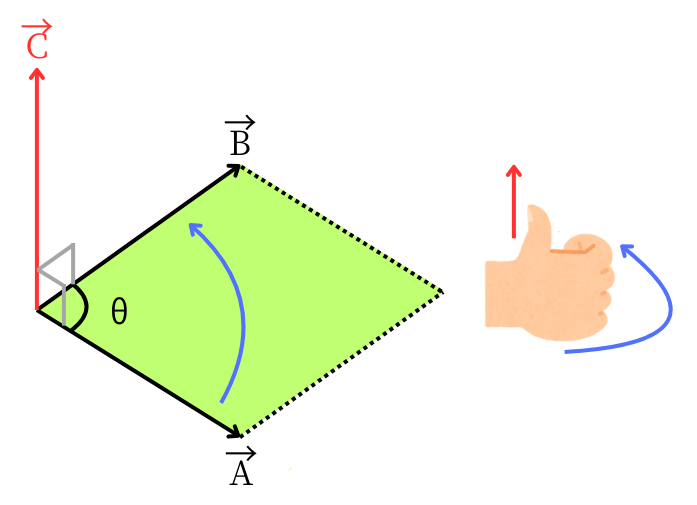
二つのベクトル\(\vec{A}\)、\(\vec{B}\)が作る外積を\(\vec{C}\)とします。
\(\vec{C}\)の向き
\(\vec{A}\)・\(\vec{B}\)の二つと直行した方向です。
そして、\(\vec{A}\)から\(\vec{B}\)に向けて右ねじの法則で回したときに、親指が向く向きと同じです。
\(\vec{C}\)の大きさ
\(\vec{C}\)の大きさは、\(\vec{A}\)と\(\vec{B}\)の作る平行四辺形の面積と同じです。つまり、
\(|C|=|A| |B| sinθ\)
です。大きさだけが欲しい場合は、スカラー表記にしてしまって
\(C=ABsinθ\)
と表すこともあります。
過去問
難易度 ★★☆☆☆
| 電験三種 令和4年度上期 問4 | ローレンツ力による起電力の計算 |
| 電験三種 令和5年度上期 問4 | 磁界と電磁力の論説 |
| 電験三種 令和5年度下期 問4 | 二つの導体に流れる電流の電磁力の計算 |
難易度 ★★★☆☆
| 電験三種 平成21年度 問12 | 電界中・磁界中の電子の動きの論説 |
| 電験三種 令和2年度 問3 | ループに及ぼす電磁力の計算 |
| 電験三種 令和4年度下期 問4 | 3つの導線が作る電磁力の計算 |
難易度 ★★★★☆
| 電験三種 令和4年度上期 問3 | 環状鉄心の結合係数の計算 |
関連記事(磁界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント