難易度
電気力線に関する基礎知識があれば解ける論説問題です。
問題の図等から、少々戸惑うかもしれませんが、冷静に問題の意図を理解できれば確実に解ける問題です。
問題
図のように、平行板コンデンサの上下極板に挟まれた空間の中心に、電荷\(Q[C]\)を帯びた導体球を保持し、上側極板の電位が\(E[V]\)、下側極板の電位が\(- E[V]\)となるように電圧源をつないだ。
ただし、\(E>0\)とする。
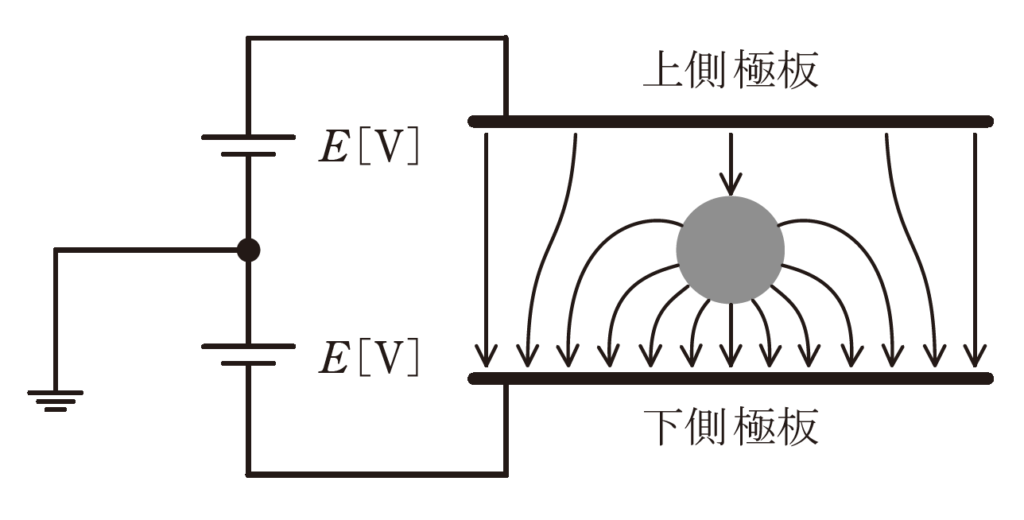
このとき,電荷Q[C]の符号と導体球の電位U[V]について,正しい記述のもの
を次の(1)~(5)のうちから一つ選べ。
(1) Q>0 であり,0<U<E である。
(2) Q>0 であり,U=E である。
(3) Q>0 であり,0<E<U である。
(4) Q<0 であり,U<- E である。
(5) Q<0 であり,- E<U<0 である。
答え
(1)
要点整理
電気力線について
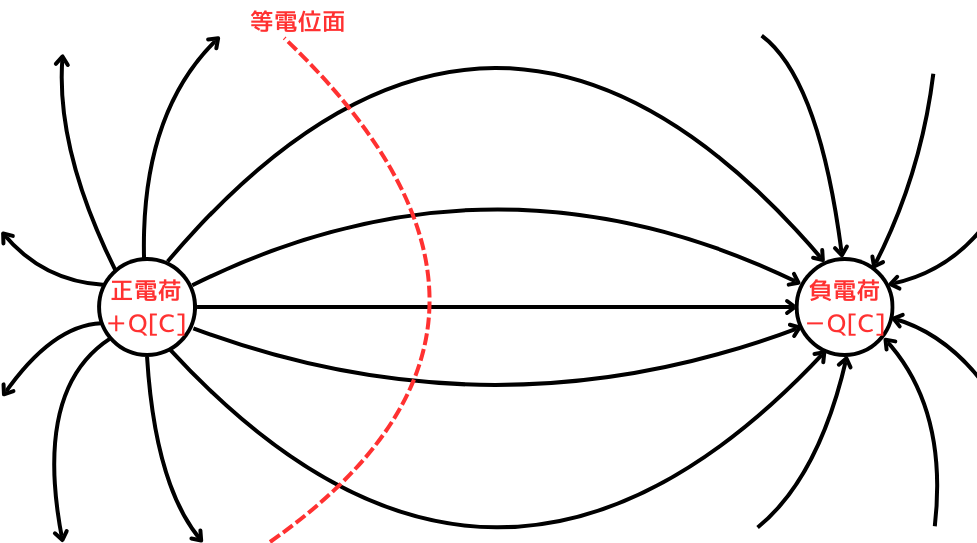
電気力線の性質
・+電荷から出て、-電荷に入る
・電荷の無い所からは発生も消失も
しない
・電気力線は交わらない
・電気力線は枝分かれしない
・電気力線は途切れない
電荷と電気力線
電荷\(Q[C]\)から出てくる電気力線の本数\(N[本]\)は、場の誘電率を\(ε[F/m]\)としたとき、
\(\displaystyle N=\frac{Q}{ε}[本]\)
です。
電気力線と電界Eの関係
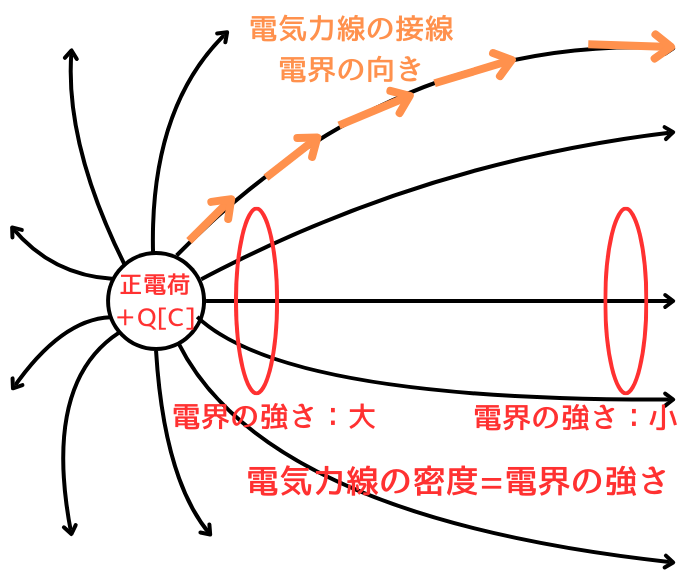
・電気力線の接線方向が、電界\(E\)の方向
・電気力線の密度が、電界の強さ\(E\)
\(\displaystyle E=\frac{N}{S}=\frac{Q}{εS}[V/m]\)
電界Eと電圧Vの関係について
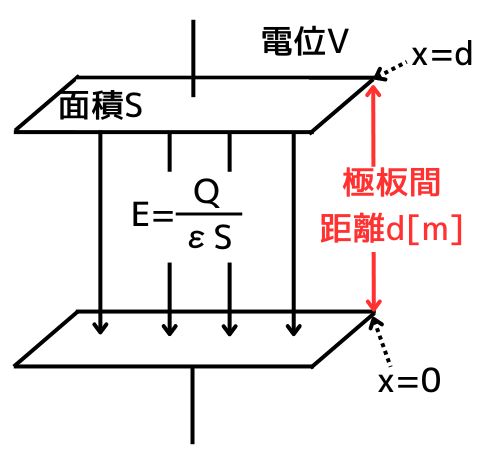
電界の強さ\(E\)と、電位\(V\)の関係は、\(V=Ed\)です。
\(V=Ed\)を導出します。
電位\(V\)は、1Cの電荷を基点から対象点へ動かすときの仕事です。
基点はコンデンサの上端で\(d[m]\)
対象点はコンデンサの下端で\(0[m]\)
としたとき、コンデンサにおける電界の強さ\(E\)と電位\(V\)の関係は次のように表されます。
\(\displaystyle \begin{eqnarray}
V&=&-\int_d^0E・dr=-E[r]_d^0=Ed\\
\end{eqnarray}\)
以上より、\(V=Ed\)が導出できました。
回答解説

電気力線の性質から
+電荷から電気力線が出て、-電荷に入ります。
このことを踏まえると、
①\(Q[C]\)を帯びた導体球から電気力線が出て\(-E\)の下側極板に入っている
②\(E[V]\)の上側極板から出た電気力線は、\(Q[C]\)を帯びた導体球を避けるようにしている
これらのことから、\(Q[C]>0\)であることがわかります。
次に、導体球の電位\(U[V]\)について考えます。
\(Q[C]>0\)であることから、導体球の電位\(U[V]\)は、\(U>0\)です。
そして、\(E[V]\)の上側極板から出た電気力線が導体球の方向に向かっていることから、\(E[V]>U[V]\)です。
以上より、電荷Q[C]の符号はQ>0 であり,電位の関係は0<U<E である(1)が答えです。
出典元
令和4年度第三種電気主任技術者試験 理論科目A問題下期問2
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント