難易度
三相交流回路の問題です。
(a)と(b)の2問あり、(a)は、相電圧と線間電圧の違いが理解できれば回答できますので、難易度は低いです。
(b)問は、Y-Δ変換について学んでおけば普通難易度の問題です。
問題
抵抗\(R[Ω]\)、誘導性リアクタンス\(X[Ω]\)からなる平衡三相負荷(力率\(80%\))に対称三相交流電源を接続した交流回路がある。次の(a)及び(b)の問に答えよ。
(a) 図1のように、Y結線した平衡三相負荷に線間電圧210Vの三相電圧を加えたとき,回路を流れる線電流\(I\) は \(\displaystyle \frac{14}{\sqrt{3}}A\) であった。
負荷の誘導性リアクタンスXの値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
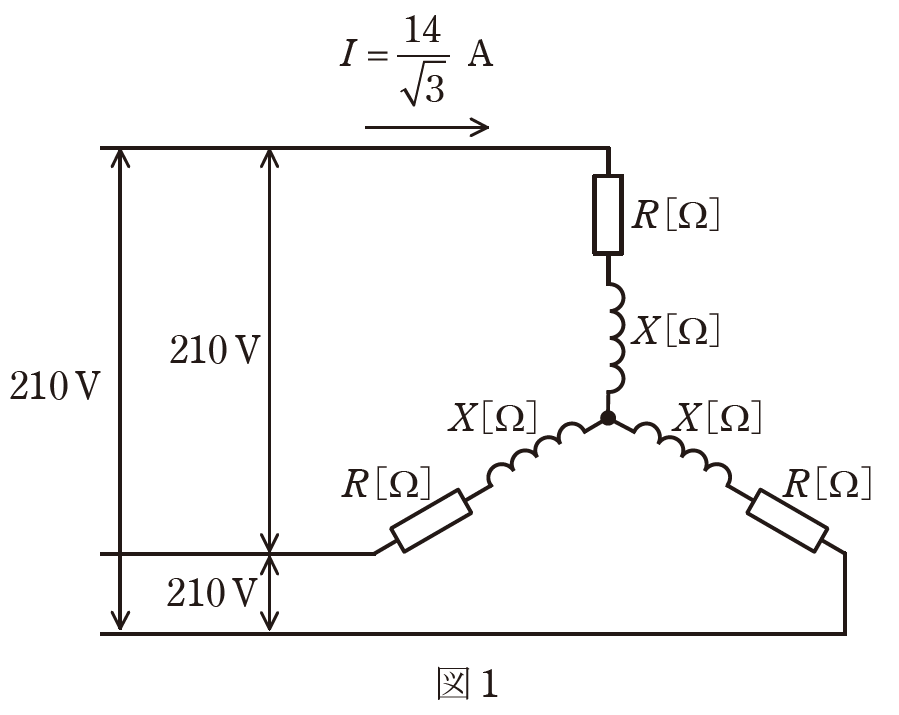
(1) 4 (2) 5 (3) 9 (4) 12 (5) 15
(b) 図1 の各相の負荷を使って結線し,図2 のように相電圧200 V の対称三相電
源に接続した。この平衡三相負荷の全消費電力の値[kW]として、最も近いもの
を次の(1)~(5)のうちから一つ選べ。
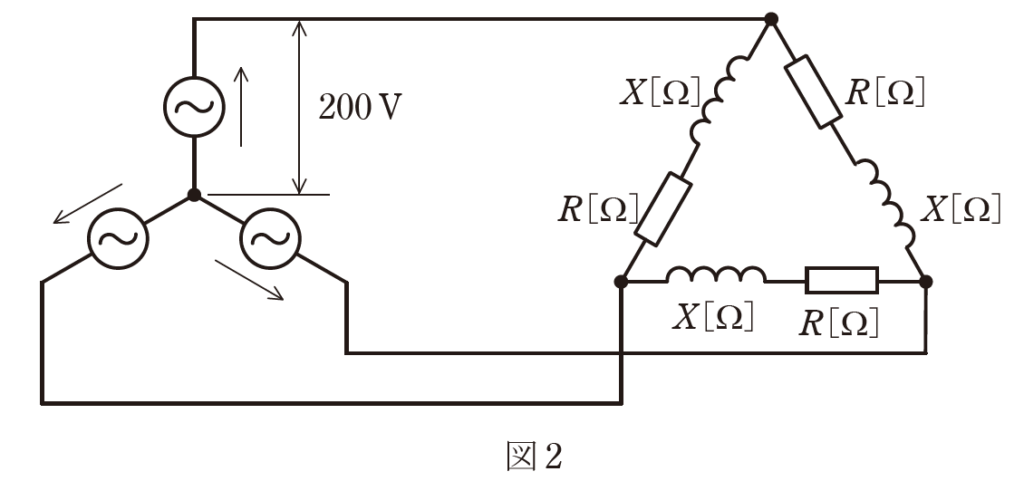
(1) 8 (2) 11.1 (3) 13.9 (4) 19.2 (5) 33.3
答え
(a) (3)
(b) (4)
要点整理
Y結線の相電圧と線間電圧
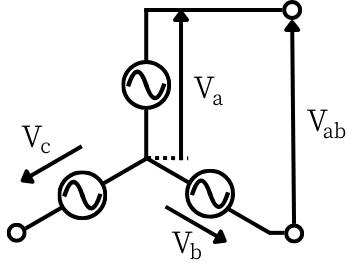
図1
左の図1のように接続したY結線の電源で、
相電圧は、\(V_a\)、\(V_b\)、\(V_c\)です。
線間電圧は、\(V_{ab}\)、\(V_{bc}\)、\(V_{ca}\)です。
相電圧と、線間電圧の関係を簡単にまとめると、
・線間電圧の大きさは、相電圧の\(\sqrt{3}\)倍の大きさです。
・線間電圧の位相は、相電圧よりも30°進んでいます。
この2つの理由について解説します。
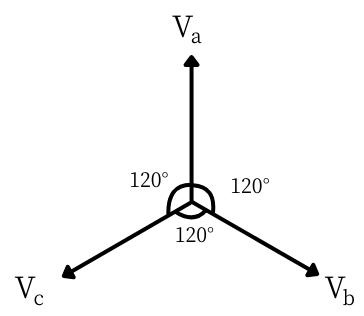
図2
三相交流の各電源\(V_a\)、\(V_b\)、\(V_c\)は、同じ大きさの電圧で、位相が120°ずつずれています。
それを図にすると、図2の通りです。
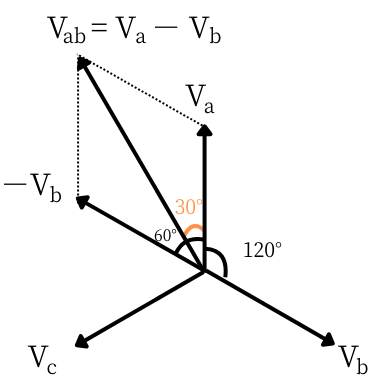
図3
線間電圧\(V_{ab}\)と相電圧\(V_a\)、\(V_b\)の関係は、
\(V_{ab}=V_a-V_b\)
です。
【電圧の大きさ】
\(-V_b\)は、\(V_b\)と真逆方向のベクトルです。
\(V_{ab}\)は、\(V_a\)と\(-V_b\)をベクトル合成したものなので、
\(\displaystyle V_{ab}=2・V_a・cos30°=2・V_a・\frac{\sqrt{3}}{2}=\sqrt{3}V_a\)
となり、線間電圧\(V_{ab}\)の大きさは、相電圧\(V_a\)の\(\sqrt{3}\)倍の大きさとなりました。
【位相差】
図3の通り、線間電圧\(V_{ab}\)の位相は、相電圧\(V_a\)よりも30°進んでいます。
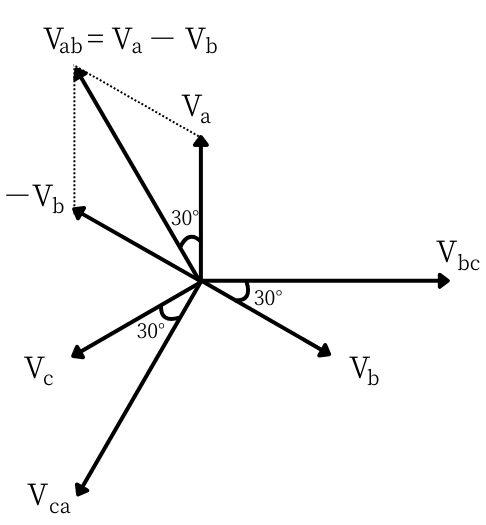
図4
線間電圧\(V_{bc}\)、\(V_{ca}\)についても、同様に求めて行くと、
線間電圧\(V_{bc}\)は、相電圧\(V_b\)に対して、
電圧の大きさは\(\sqrt{3}\)倍、位相は30°進みです。
線間電圧\(V_{ca}\)は、相電圧\(V_c\)に対して、
電圧の大きさは\(\sqrt{3}\)倍、位相は30°進みです。
以上をベクトル図に示すと、図4の通りです。
Δ結線の相電流と線電流
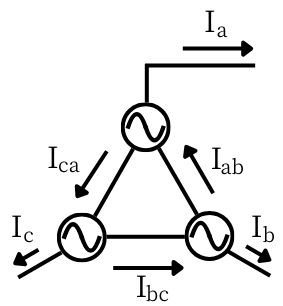
図1
左の図1のように接続したΔ結線の電源で、
相電流は、\(I_{ab}\)、\(I_{bc}\)、\(I_{ca}\)です。
線電流は、\(I_a\)、\(I_b\)、\(I_c\)です。
相電流と、線電流の関係を簡単にまとめると、
・線電流の大きさは、相電流の(\sqrt{3}\)倍の大きさです。
・線電流の位相は、相電流よりも30°遅れています。
この2つの理由について解説します。
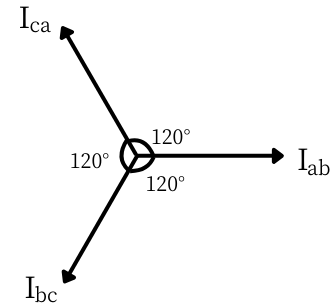
図2
\(I_{ab}\)、\(I_{bc}\)、\(I_{ca}\)は、同じ大きさの電流で、位相が120°ずつずれています。
それを図にすると、図2の通りです。
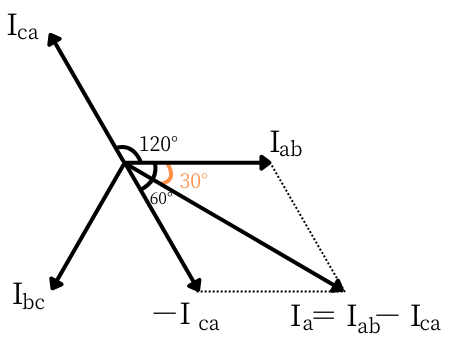
図3
線電流\(I_a\)と相電流\(I_{ab}\)、\(I_{ca}\)の関係は、キルヒホッフの電流則から、
\(I_a=I_{ab}-I_{ca}\)
です。
【電流の大きさ】
\(-I_{ca}\)は、\(I_{ca}\)と真逆方向のベクトルです。
\(I_{ab}\)は、\(I_{ab}\)と\(-I_{ca}\)のベクトル合成です。
\(\displaystyle I_a=2・I_{ab}・cos30°=2・I_{ab}・\frac{\sqrt{3}}{2}=\sqrt{3}I_{ab}\)
となり、線電流\(I_a\)の大きさは、相電流\(I_{ab}\)の\(\sqrt{3}\)倍の大きさとなりました。
【位相差】
左図の通り、線電流\(I_a\)の位相は、相電流\(I_{ab}\)よりも30°遅れています。
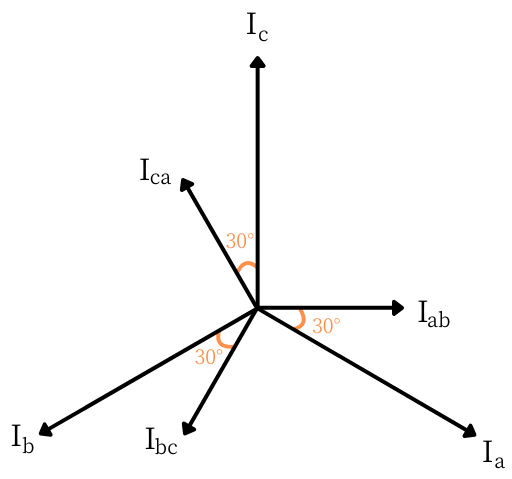
図4
線電流\(I_b\)、\(I_c\)についても、同様に求めて行くと、
線電流\(I_b\)は、相電流\(I_{bc}\)に対して、
電流の大きさは\(\sqrt{3}\)倍、位相は30°遅れです。
線電流\(I_c\)は、相電流\(I_{ca}\)に対して、
電流の大きさは\(\sqrt{3}\)倍、位相は30°遅れです。
以上をベクトル図に示すと、図4の通りです。
インピーダンス Z ・ レジスタンス R ・ リアクタンス X
直流回路では、電流を流れにくくする要素は、レジスタンス(抵抗)のみを考えていれば十分でした。しかし、交流回路ではインピーダンス\(Z\)、レジスタンス\(R\)、リアクタンス\(X\)の3つを考える必要があります。
\(Z、R、X\)の関係は、\(Z=R+jX\)です。
式中のjは虚数単位であり、\(j^2=−1\)です。
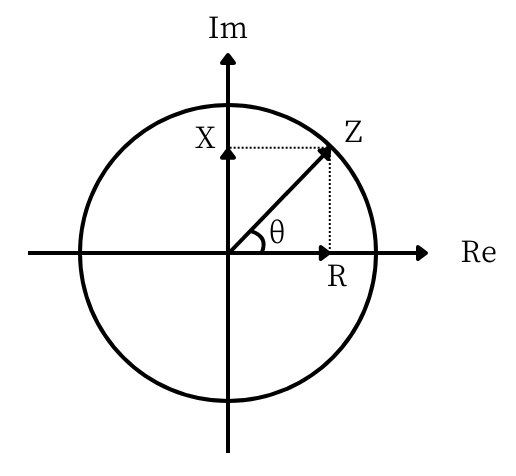
\(Z、R、X\)の関係を複素数平面図に表すと、左図のようになります。
\(Re\)と記載した横軸は、実軸(Real axis)
\(Im\)と記載した縦軸は、虚軸(Imaginary axis)
です。
左図からわかる通り
\(R=Zcosθ\)
\(X=Zsinθ\)
です。
\(cosθ\)は、力率と呼ばれます。
力率は1.0に近い程効率良く電力を送電できます。
三平方の定理から、
\(Z=\sqrt{R^2+X^2}\)
の関係もあります。
Y-Δ変換
三相交流の解析をする際、Δ結線では扱い難い場合、Y結線では扱い難い場合があります。
その時に、Y-Δ変換をしてΔ結線をY結線に変換する、逆にY結線をΔ結線に変換することで、問題を解決しやすくなります。
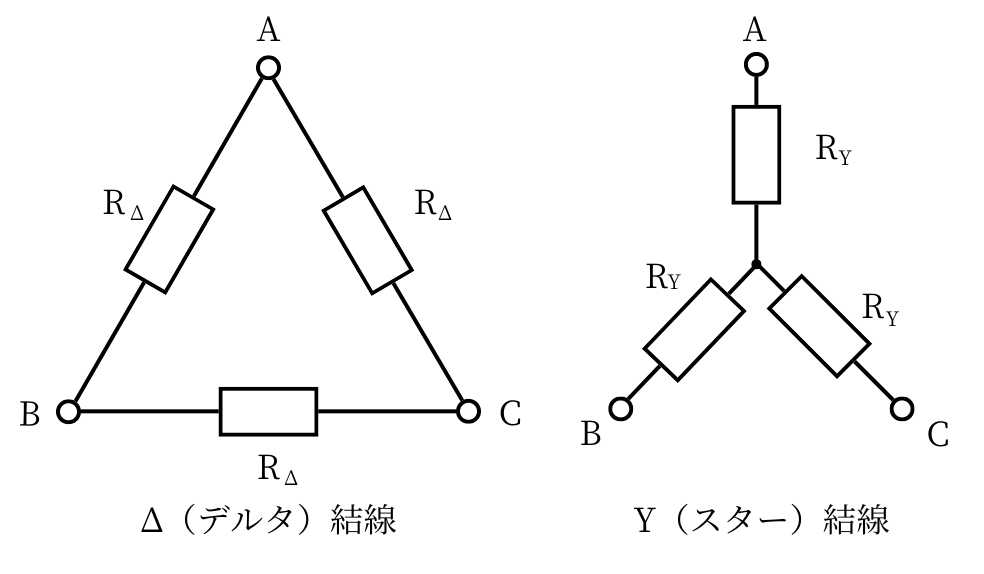
Δ結線の抵抗を\(R_\Delta\)
Y結線の抵抗を\(R_Y\)
とし、AB間、BC間、CA間の抵抗が全て同じ抵抗値の物が接続されているとします。
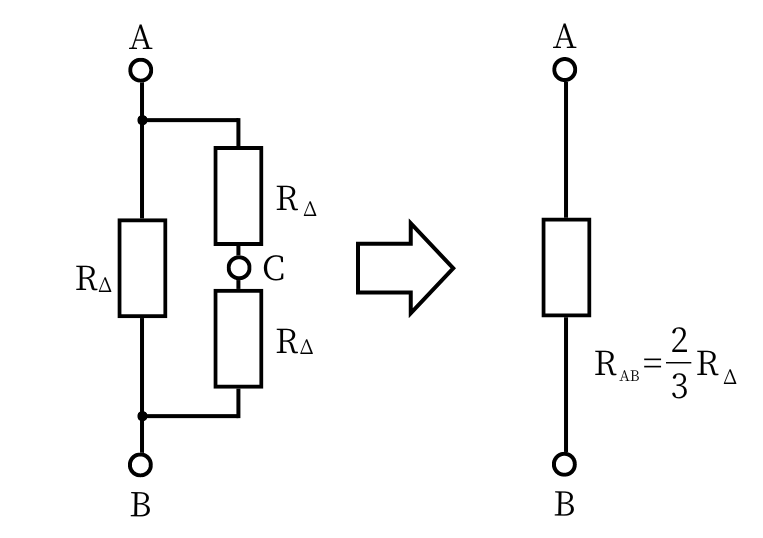
まずは、Δ結線のAB間の抵抗について検討します。
Δ結線のAB間の抵抗を\(R_{AB}\)としたとき、
\(\displaystyle \frac{1}{R_{AB}}=\frac{1}{R_\Delta}+\frac{1}{2R_\Delta}=\frac{3}{2R_\Delta}\)
⇔\(\displaystyle R_{AB}=\frac{2R_\Delta}{3}\) ……①
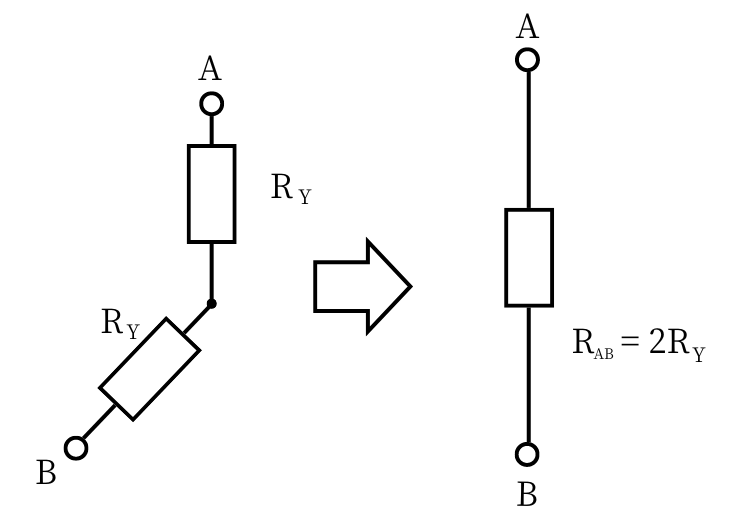
次に、Y結線のAB間の抵抗について検討します。
Y結線のAB間の抵抗も同じく\(R_{AB}\)とすると、
\(R_{AB}=2R_Y\) ……②
となります。
最後に、①=②より、
\(\displaystyle \frac{2R_\Delta}{3}=2R_Y\)
したがって、
\(R_\Delta=3R_Y\)
⇔\(\displaystyle R_Y=\frac{1}{3}R_\Delta\)
の関係が導き出せます。
注意点としては、全ての抵抗が同じ抵抗という前提の元、簡略化しています。
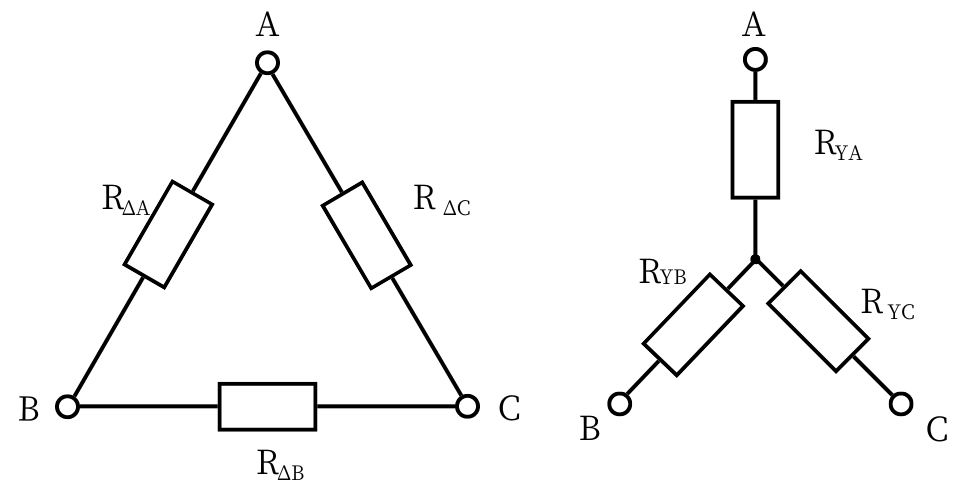
全部の抵抗値が違う場合のY-Δ変換の公式は、
\(\displaystyle R_{YA}=\frac{R_{\Delta B}R_{\Delta C}}{R_{\Delta A}+R_{\Delta B}+R_{\Delta C}}\)
\(\displaystyle R_{YB}=\frac{R_{\Delta C}R_{\Delta A}}{R_{\Delta A}+R_{\Delta B}+R_{\Delta C}}\)
\(\displaystyle R_{YC}=\frac{R_{\Delta A}R_{\Delta B}}{R_{\Delta A}+R_{\Delta B}+R_{\Delta C}}\)
です。導出するのは手間なので、ここでは割愛します。
\(R_{\Delta A}=R_{\Delta B}=R_{\Delta C}=R_{\Delta }\)とした場合、
\(\displaystyle R_Y=\frac{1}{3}R_\Delta\)
が成り立つことがわかると思います。
回答解説
問(a)

問題の図1から、線間電圧が210Vです。
相電圧\(V\)は、Y結線の相電圧と線間電圧の関係から\(\displaystyle V=\frac{210}{\sqrt{3}}[V]\)です。
線電流は\(\displaystyle I=\frac{14}{\sqrt{3}}[A]\)です。
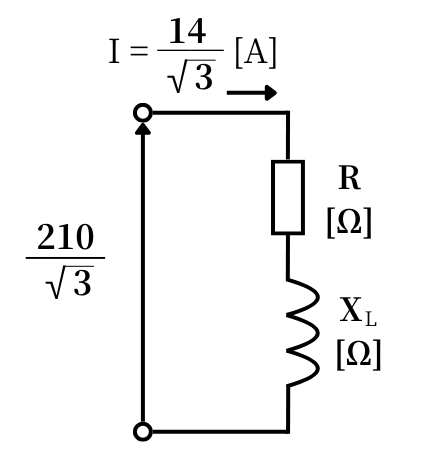
相電圧と線電流をまとめて表すと左図のようになります。
インピーダンス\(Z\)を求めると、
\(\displaystyle Z=\frac{V}{I}=\frac{\frac{210}{\sqrt{3}}}{\frac{14}{\sqrt{3}}}=\frac{210}{14}=15[Ω]\)です。
問題文から、力率\(cosθ=0.8\)ですので、
\(cos^2θ+sin^2θ=1\)
⇔\(sinθ=\sqrt{1-cos^2θ}=\sqrt{1-0.8^2}=\sqrt{0.36}=0.6\)
したがって、リアクタンス\(X[Ω]\)は、
\(X=Zsinθ=15・0.6=9[Ω]\)です。
以上より、(3)9 が答えです。
問(b)
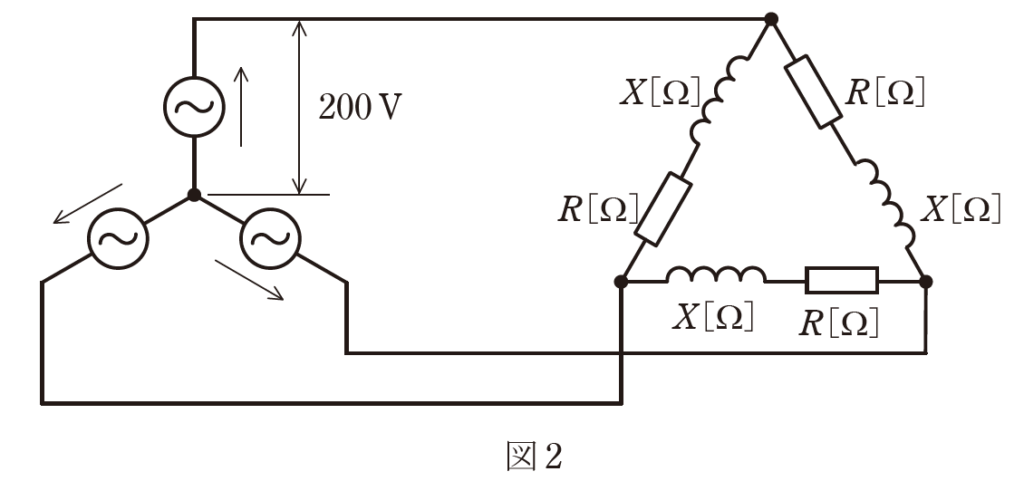
問題の図2は、電源がY結線、負荷がΔ結線で問題を解くのが難しいです。
そのため、負荷のΔ結線をY結線に変換することで解きやすくします。
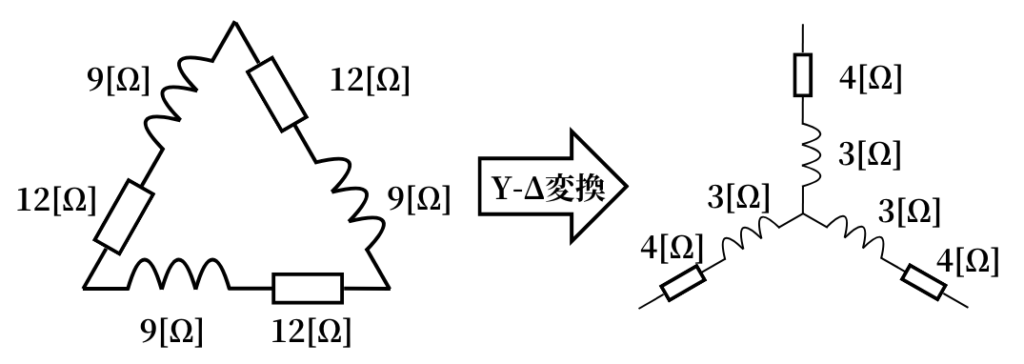
Y-Δ変換は、
\(\displaystyle R_Y=\frac{1}{3}R_\Delta\)
なので、
Δ結線からY結線にするときは、\(\frac{1}{3}\)倍にします。
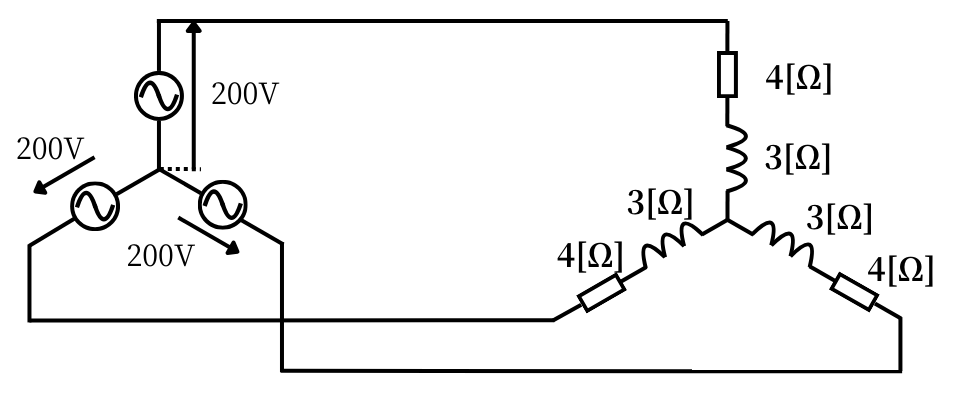
問題の回路をΔ-Y変換した後の回路は、左図のとおりです。
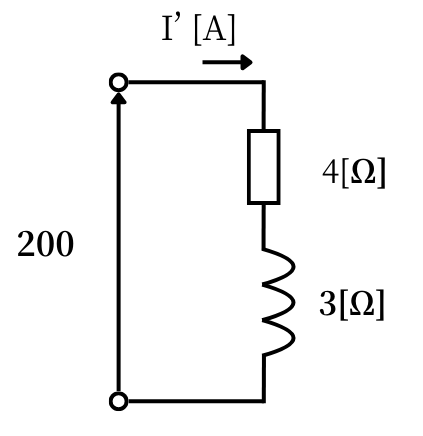
三相回路から、1相分だけ取り出します。
電流の大きさ\(|I’|\)は、
\(\displaystyle |I’|=\frac{V}{|Z|}=\frac{200}{\sqrt{4^2+3^2}}=40[A]\)
電流\(I’=40[A]\)で、抵抗\(R=4[Ω]\)なので、
1相分の消費電力は、
\(P_1=I’^2R=40^2・4=6400=6.4[kW]\)
です。
本問の回路は三相交流なので、三相全ての消費電力を考慮するために3倍する必要があります。したがって、
\(P=3P_1=3・6.4=19.2[kW]\)
となります。したがって、回答は(4)19.2 です。
出典元
令和5年度第三種電気主任技術者試験 理論科目B問題下期問15
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント