【電験三種：理論】平成２１年度　問１８

難易度

エミッタ接地のトランジスタ増幅器の小信号等価回路の問題です。
電子回路の問題難しい単元であることから、しっかりと学習して挑む必要があります。
本問のｈパラメータの問題は、各パラメータについての理解を要します。
また、回路中に電流源が出てくるため、馴染みが無いうちは、扱い難い回路です。

試験までの学習時間が取れない場合は捨て問題としても良いかもしれません。

問題

図１の回路は、エミッタ接地のトランジスタ増幅器の交流小信号に注目した回路である。次の(a)及び(b)に答えよ。
ただし、$R_L[Ω]$は抵抗、$i_b[A]$は入力信号電流、$i_c=6×10^{-3}[A]$は出力信号電流、$v_b[V]$は入力信号電圧、$v_c=6[V]$は出力信号電圧である。

---

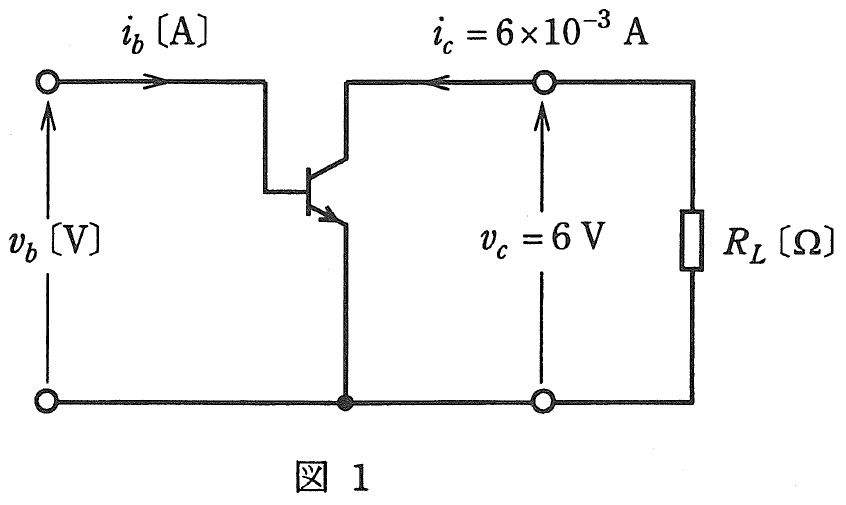
(a)図１の回路において、入出力信号の関係を表１に示すｈパラメータを用いて表すと次の式①、②になる。

$v_b=h_{ie}i_b+h_{re}v_c$　　　………①
$i_c=h_{fe}i_b+h_{oe}v_c$　　　………②

表１　ｈパラメータの数値例

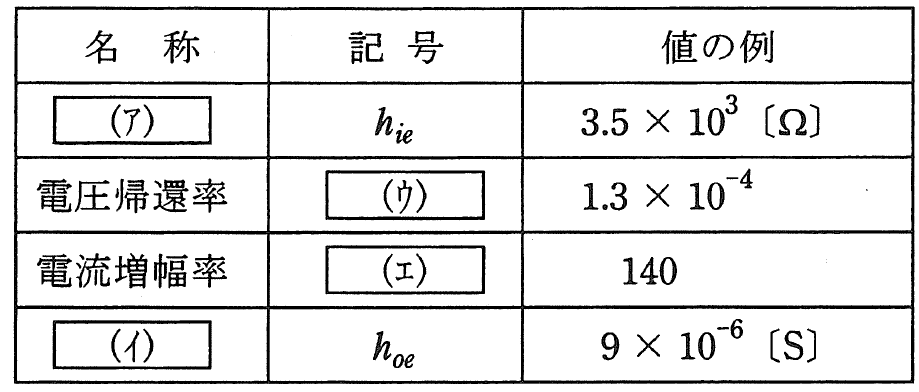
上記表中の空白箇所（ア）、（イ）、（ウ）及び（エ）に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。

	（ア）	（イ）	（ウ）	（エ）
（１）	入力インピーダンス	出力アドミタンス	$h_{fe}$	$h_{re}$
（２）	入力コンダクタンス	出力インピーダンス	$h_{fe}$	$h_{re}$
（３）	出力コンダクタンス	入力インピーダンス	$h_{re}$	$h_{fe}$
（４）	出力インピーダンス	入力コンダクタンス	$h_{re}$	$h_{fe}$
（５）	入力インピーダンス	出力アドミタンス	$h_{re}$	$h_{fe}$

---

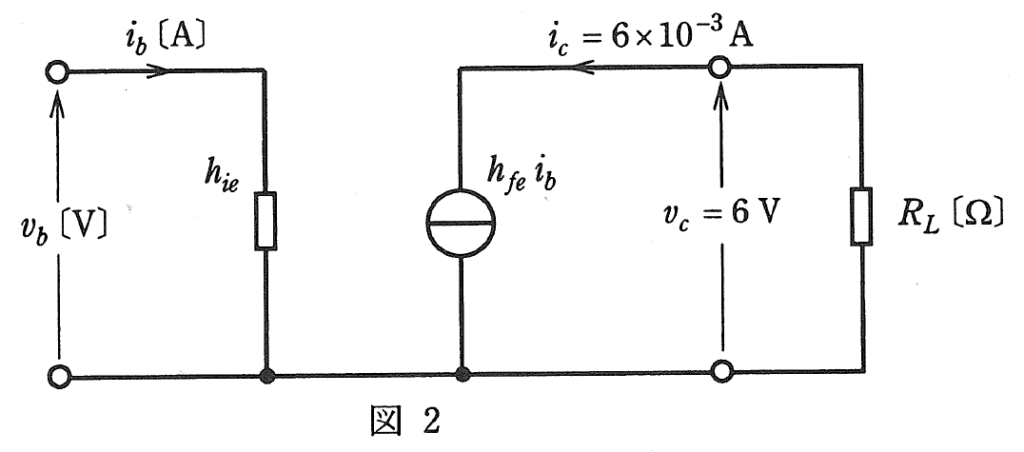
(b)図１の回路の計算は、図２の簡易小信号等価回路を用いて行うことが多い。
この場合、上記(a)の式①、②から求めた$v_b[V]$及び$i_b[A]$の値をそれぞれ真の値としたとき、図２の回路から求めた$v_b[V]$及び$i_b[A]$の誤差$Δv_b[mV]$、$Δi_b[μA]$の大きさとして、最も近いものを組み合わせたのは次のうちどれか。
ただし、ｈパラメータの値は表１に示された値とする。

	$Δv_b$	$Δi_b$
（１）	0.78	54
（２）	0.78	6.5
（３）	0.57	6.5
（４）	0.57	0.39
（５）	0.35	0.39

---

答え

問(a)　(5)
問(b)　(4)

回答方針

(a)
知識問題ですが、分かり易いものから推測していきます。
（ア）は数値の単位$[Ω]$から、インピーダンスと推測できます。
　　　また、入力信号$v_b、i_b$に繋がっているため、入力インピーダンスだとわかります。
（イ）は数値の単位$[S]$から、アドミタンスと推測できます。
　　　この時点で(1)と(5)の二択になります。
（エ）は電流源のシンボルに$h_{fe}$があることから、電流増幅率が$h_{fe}$と推測できます。

(b)
①問題文で示されたｈパラメータの式に与えられた条件を代入し、$v_b$、$i_b$を求める。
②問題文図２から、式を組み立てて、$v_b$、$i_b$を求める。
③それぞれの$v_b$、$i_b$を比較し、$Δv_b$、$Δi_b$を求める。

要点整理　問(a)

ｈパラメータ

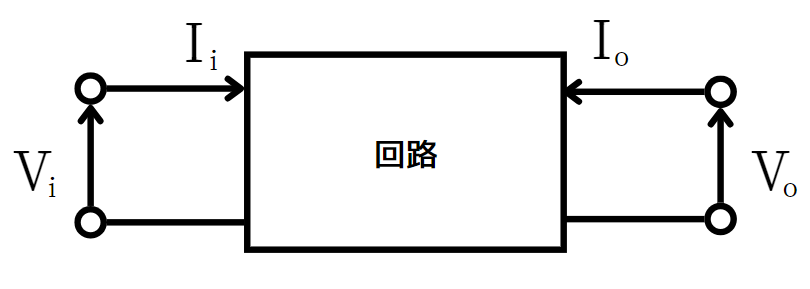
上図は、２端子対回路といいます。
これは、対象の回路をブラックボックスとして取り扱い、入力電圧$V_i$、入力電流$I_i$、出力電圧$V_o$、出力電流$I_o$の４つの入出力の関係だけで表すようにしたものです。
本問では、トランジスタをブラックボックスの回路として２端子対回路としています。

そして、ｈパラメータは、この入出力の関係を表すのに必要な係数です。

左図の回路を、ｈパラメータを使って表すと、
$\begin{bmatrix}V_i \\ I_o \end{bmatrix}= \begin{bmatrix} h_i & h_r \\ h_f & h_o \end{bmatrix} \begin{bmatrix} I_i \\ V_o \end{bmatrix}$
となります。

これらの係数を整理します。
・$h_i=\frac{V_i}{I_i}$は、入力インピーダンスです。
　添え字の i は、Input（入力）を表します。

・$h_r=\frac{V_i}{V_o}$は、電圧帰還率です。
　添え字の r は、Reverse（逆）を表します。

・$h_f=\frac{I_o}{I_i}$は、電流増幅率です。
　添え字の f は、Forward（順方向）を表します。

・$h_o=\frac{I_o}{V_o}$は、出力アドミタンスです。
　添え字の o は、Output（出力）を表します。

本問のように、エミッタ接地回路の場合は、
添え字に e を追加し、$h_{ie},h_{re},h_{fe},h_{oe}$とします。 e はEmitter（エミッタ）を表します。

要点整理　問(b)

問題文中の回路図について

問題文中の①・②式が描くべき回路図と、問題文中の図２に示される回路図は異なります。
問題文中の図２の回路図は、影響が小さな$h_{re}$と、$h_{oe}$の２つを簡略化し、計算しやすいようにしています。

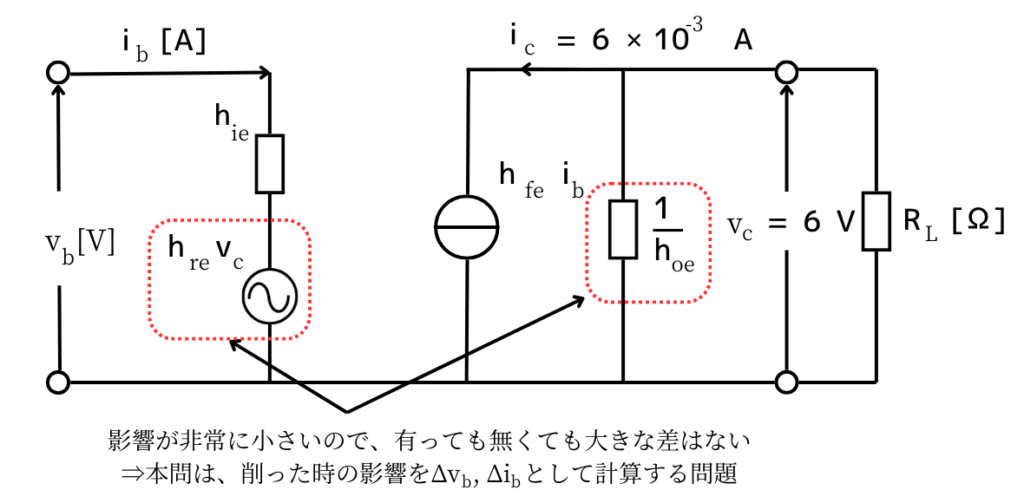
問題文中に示された式
$v_b=h_{ie}i_b+h_{re}v_c$　　　………①
$i_c=h_{fe}i_b+h_{oe}v_c$　　　………②
が描く回路図は、上図の通りです。

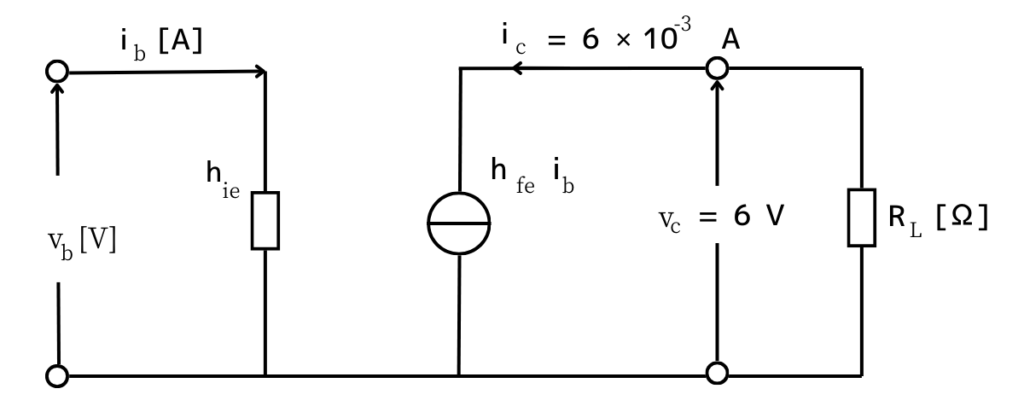
問題文の図２に示される図を示します。
$h_{re}$と$h_{oe}$が省略されていることがわかります。
省略された２つは、省略しても影響が非常に小さいため、厳密に計算する必要が無い場合は省略しても問題はないです。
この回路図から導き出される式は、
$v_b=h_{ie}i_b$　　　………③
$i_c=h_{fe}i_b$　　　………④
です。
その差$Δv_b,Δi_b$は、以下の通りとなります。
$Δv_b=①式-③式=h_{re}v_c$　　　………⑤
$Δi_b=②式-④式=h_{oe}v_c$　　　………⑥

簡易小信号等価回路の動作概要

小信号等価回路は、初見では中々わかりづらいので、見方の概要を整理します。

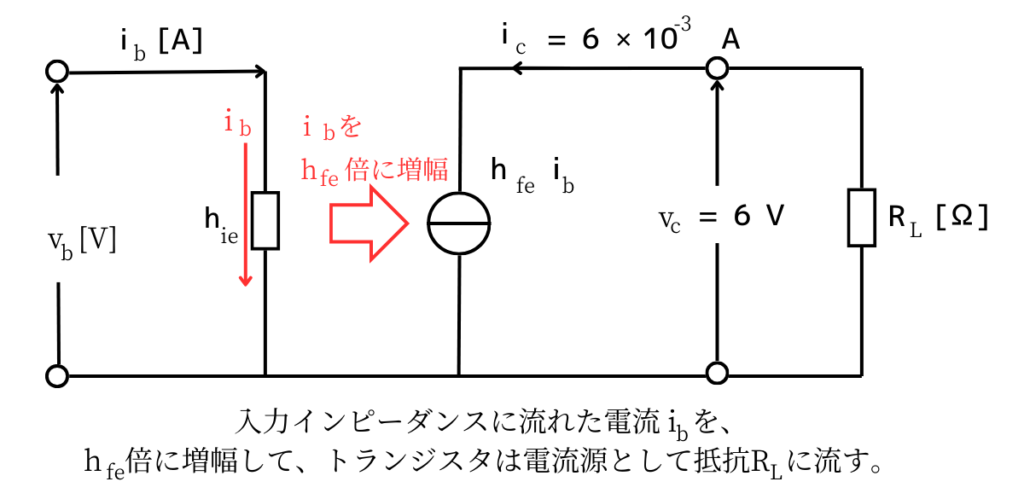
入力信号$v_b$は、トランジスタの入力インピーダンス$h_{ie}$に、電流$i_b$を流します。
この時、流れる電流はオームの法則から
$\displaystyle i_b=\frac{v_b}{h_{ie}}$
です。入力インピーダンスは大きい抵抗値を示すため、流れる電流は非常に小さいです。

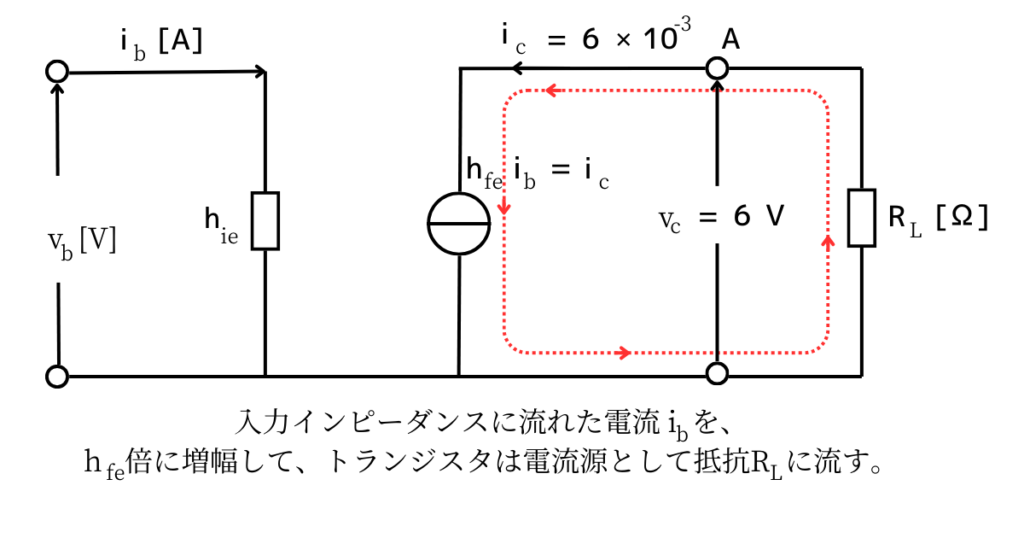
電流増幅率$h_{fe}$倍に増幅された電流$h_{fe}i_b$を、電流源として出力します。

出力電流$i_c$は、入力電流$i_b$と、電流増幅率$h_{fe}$で決まるため、出力に接続された抵抗$R_L[Ω]$の抵抗の大きさによらず一定です。
そして、出力電圧$v_c$は、$R_L$が大きければ、大きな出力電圧$v_c$を得る事ができます。
つまり、抵抗$R_L$の大きさによって、電圧利得を変化させることができます。

要点整理の適用　問(a)

要点整理のhパラメータの項目で記載した通り、

名称	記号	値の例
(ア)入力インピーダンス	$h_{ie}$	$3.5×10^{-3}[Ω]$
電圧帰還率	(ウ)$h_{re}$	$1.3×10^{-4}$
電流増幅率	(エ)$h_{fe}$	$140$
(イ)出力アドミタンス	$h_{oe}$	$9×10^{-6}[S]$

以上より、答えは(5)とわかります。

要点整理の適用　問(b)

問題文中に示された式は①②式です。
$v_b=h_{ie}i_b+h_{re}v_c$　　　………①
$i_c=h_{fe}i_b+h_{oe}v_c$　　　………②

①②式に、各数値を代入し計算していきます。
まずは、②式から、
$i_c=h_{fe}i_b+h_{oe}v_c$　
⇔$\displaystyle i_b=\frac{i_c-h_{oe}v_c}{h_{fe}}$
⇔$\displaystyle i_b=\frac{6×10^{-3}-54×10^{-6}}{140}$
⇔$i_b=42.471×10^{-6}[A]=42.471[μA]$

次に、①式から、
$v_b=h_{ie}i_b+h_{re}v_c$
⇔$v_b=3.5×10^3・42.471×10^{-6}+7.8×10^{-4}$
⇔$v_b=148.65×10^{-3}+0.78×10^{-4}$
⇔$v_b=149.43×10^{-3}[V]=149.43[mV]$

次に図２の回路図から、式を立てて計算していきます。

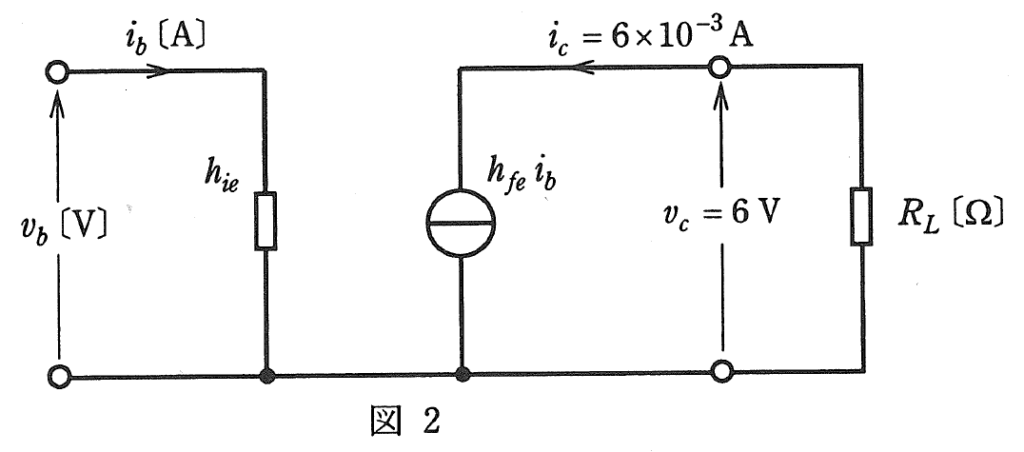
図２から、下記③④式が立てられます。
$v_b=h_{ie}i_b$　　　………③
$i_c=h_{fe}i_b$　　　………④

④式から、
$\displaystyle i_b=\frac{i_c}{h_{fe}}=\frac{6×10^{-3}}{140}$
⇔$i_b=42.857×10^{-6}[A]=42.857[μA]$

③式から、
$v_b=h_{ie}i_b=3.5×10^3・42.857×10^{-6}$
⇔$v_b=150.00×10^{-3}[V]=150.00[mV]$

以上より、
$Δv_b=150.00-149.43=0.57[mV]$
$Δi_b=42.857-42.471=0.386≒0.39[μA]$

となります。したがって、答えは(4)です。

出典元

平成２１年度第三種電気主任技術者試験　理論科目B問題問１８

参考書