難易度
平行平板コンデンサの問題で、簡単な部類の問題です。
問(a)は、電界\(E\)に関する式を理解していれば解けます。
問(b)は、電圧\(V\)と電界\(E\)の関係を理解していれば解けます。
B問の選択問題としては、ボーナス問題とも言えるので、確実に完答したい問題です。
問題
図に示すように、面積が十分広い平行平板電極（電極間距離10[mm]）が空気（比誘電率\(ε_{r1}=1\)とする。）と、電極と同形同面積の厚さ4[mm]で比誘電率\(ε_{r2}=4\)の固体誘電体で構成されている。下部電極を接地し、上部電極に直流電圧\(V[kV]\)を加えた。次の(a)及び(b)に答えよ。
ただし、固体誘電体の導電性及び電極と固体誘電体の端効果は無視できるものとする。
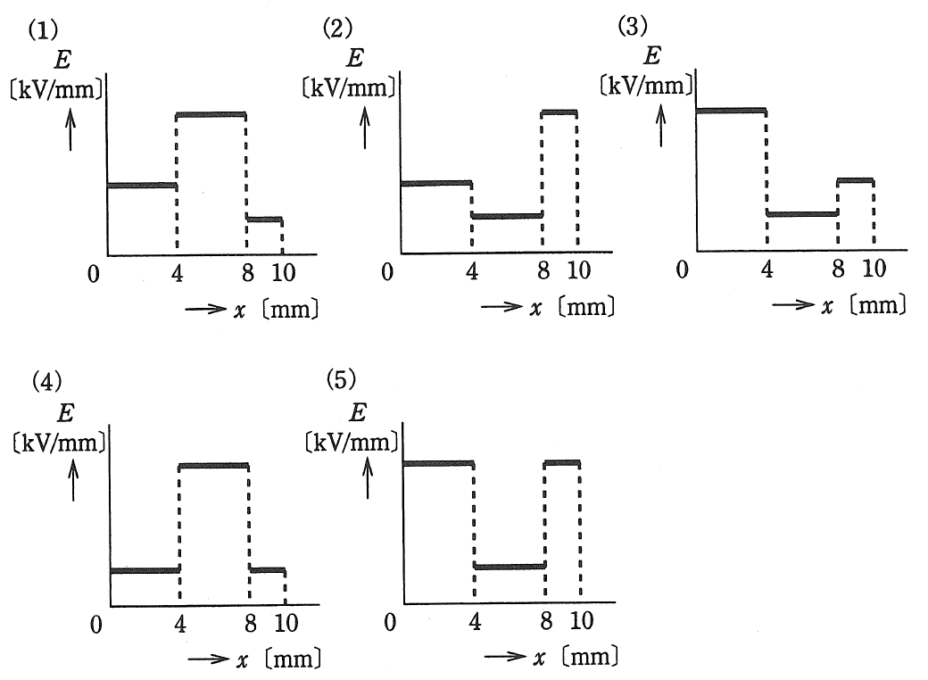
(a)電極間の電界の強さ\(E[kV/mm]\)のおおよその分布を示す図として、正しいのは次のうちどれか。
ただし、このときの電界の強さでは、放電は発生しないものとする。また、各図において、上部電極から下部電極に向かう距離を\(x[mm]\)とする。
(b)上部電極に加える電圧\(V[kV]\)を徐々に増加し、下部電極側の空気中の電界の強さが\(2[kV/mm]\)に達したときの電圧\(V[kV]\)の値として、正しいのは次のうちどれか。
| (1) 11 | (2) 14 | (3) 20 | (4) 44 | (5) 56 |
答え
問(a) (5)
問(b) (2)
回答方針
(a)
①空気・固体誘電体・空気のコンデンサの直列接続として考えます。
②各コンデンサには、全て同じ電荷\(Q\)が充電されます。
③電界の式\(E=\frac{Q}{εS}\)から、電界の分布を描きます。
(b)
①電圧と電界の関係式\(V=Ed\)から、空気層、誘電体層、空気層の各層の電圧を計算します。
②各層の電圧を足すと、上部電極に加える電圧\(V\)が求まります。
要点整理 問(a)
コンデンサの直列接続について
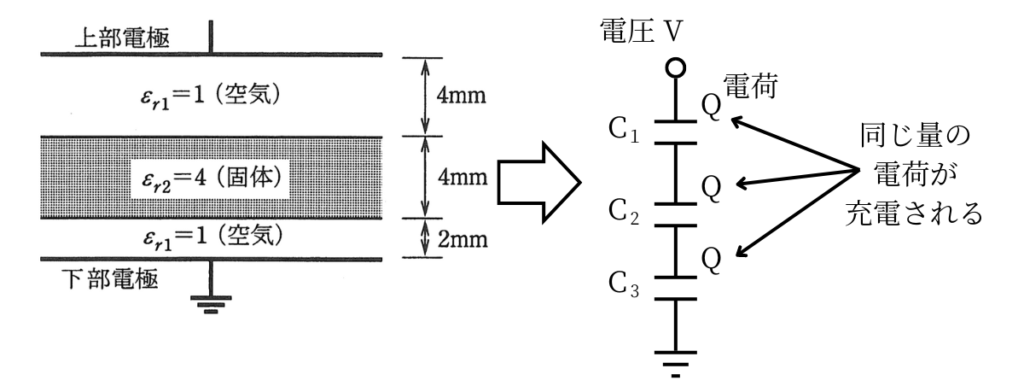
本問のように、空気層＋固体誘電体層＋空気層で構成されるコンデンサでは、コンデンサが３つ直列接続されていると考えます。
直列されたコンデンサに電圧\(V\)が印加されたとき、各コンデンサには全て同じ電荷\(Q\)が充電されます。
コンデンサの電界の強さについて
| 電界の強さは、1Cの電荷を置いたときに場から受ける力であり、\(\displaystyle E=\frac{Q}{εS}\)で表されます。 この式の成り立ちについて整理します。 電荷\(Q[C]\)が出す電気力線の本数は\(\displaystyle N=\frac{Q}{ε}[本]\)です。 電界の強さ\(E\)は、電気力線の密度と等しいので、電気力線の本数\(N\)を面積\(S\)で割って \(\displaystyle E=\frac{Q}{εS}\)となります。 点電荷の場合は、電荷から距離が離れるにしたがって、球の表面積\(S=4\pi r^2\)で広くなっていくので、 \(\displaystyle E=\frac{Q}{4\pi ε r^2}\) と表されます。この式は、静電界の問題を取り組んでいると何度か見る事があるでしょう。 | |
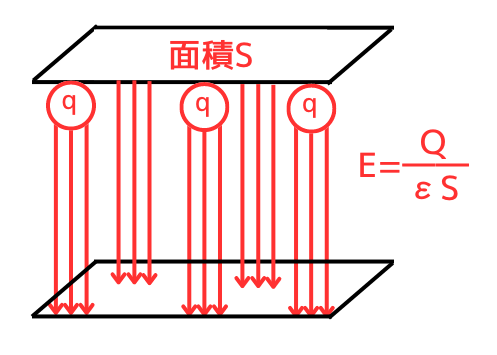 | 次に、平行平板コンデンサの場合の電界の強さ\(E\)は、点電荷の場合と同じく \(\displaystyle E=\frac{Q}{εS}\) です。しかし、点電荷と違って、広がりが無く、一様な電界となります。そのため、コンデンサは距離が離れても極板面積\(S\)は変わりません。 したがって、極板面積\(S\)が与えられていれば、電荷\(Q\)がわかれば、電界の強さ\(E\)は求まります。 |
要点整理 問(b)
電位Vと電界の強さEについて
電界の強さは、1Cの電荷を置いたときに場から受ける力です。
電位は１Cの電荷を基点から対象点へ動かすときの仕事であり、基点が定義されていないときは、無限遠点を基点とします。電界の強さ\(E\)と電位\(V\)の関係は次のように表されます。
\(\displaystyle V=-\int_{無限遠点}^{対象点}E・dr\)
この式から、点電荷の時、コンデンサの時の２つの場合において、電位Vと電界の強さEの関係式が異なってくることがわかります。
| 点電荷の場合 対象点をr、基準点を∞とすると、 \(\displaystyle V=-\int_{∞}^{r} E・dr=-\int_{∞}^{r}\frac{Q}{4\pi ε r^2}dr\) \(\displaystyle =-\frac{Q}{4\pi ε}\left[-\frac{1}{r}\right]_∞^r=\frac{Q}{4\pi εr}\) したがって、 \(\displaystyle V=\frac{Q}{4\pi εr}\) となります。 | |
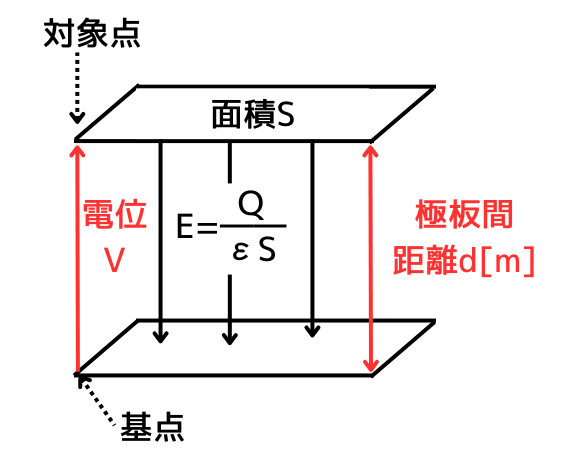 | コンデンサの場合 対象点を0、基準点をd[m]とすると、 \(\displaystyle V=-\int_{d}^{0} E・dr=-\int_{d}^{0}\frac{Q}{εS}dr\) \(\displaystyle =-\frac{Q}{εS}[r]_d^0=Ed\) したがって、 \(V=Ed\) となります。 |
要点整理の適用 問(a)
要点整理のコンデンサの直列接続についての項目で記載したとおり、
空気層＋固体誘電体層＋空気層の直列接続として考えると直列されたコンデンサに電圧Vが印加されたとき、各コンデンサには全て同じ電荷\(Q\)が充電されます。
電界の式\(\displaystyle E=\frac{Q}{εS}\)から、
\(C_1\)コンデンサ（空気層）の電界\(\displaystyle E_1=\frac{Q}{ε_{r1}ε_0S}=\frac{Q}{ε_0S}\)
\(C_2\)コンデンサ（固体誘電体層）の電界\(\displaystyle E_2=\frac{Q}{ε_{r2}ε_0S}=\frac{Q}{4ε_0S}=\frac{1}{4}E_1\)
\(C_3\)コンデンサ（空気層）の電界\(\displaystyle E_3=\frac{Q}{ε_{r1}ε_0S}=\frac{Q}{ε_0S}=E_1\)
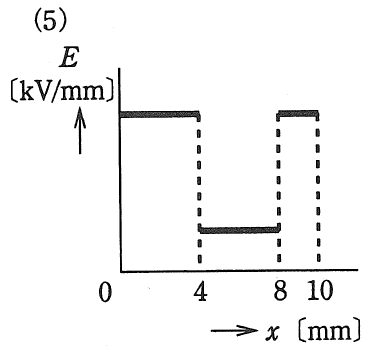
この計算結果を分布図に示すと、(5)の分布図の通りとなります。
要点整理の適用 問(b)
電位Vと電界の強さEの関係は、要点整理で示した通り、\(V=Ed\)です。
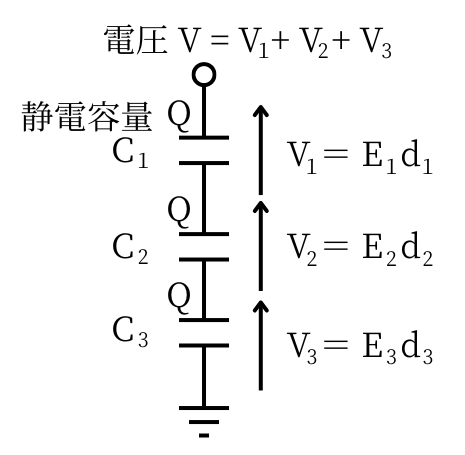 | 問題文より、下部電極側の空気中の電界の強さが\(E=2[kV/mm]\)です。 問(a)より、 \(E_1=E=2[kV/mm]\) \(E_2=\frac{1}{4}E=0.5[kV/mm]\) \(E_3=E_1=2[kV/mm]\) です。 問題文中の図より、 \(d_1=4[mm]\)、\(d_2=4[mm]\)、\(d_3=2[mm]\)です。 以上より、 \(V_1=E_1・d_1=2[kV/mm]・4[mm]=8[kV]\) \(V_2=E_2・d_2=0.5[kV/mm]・4[mm]=2[kV]\) \(V_3=E_3・d_3=2[kV/mm]・2[mm]=4[kV]\) したがって、印加した電圧は、 \(V=V_1+V_2+V_3=14[kV]\) となります。 したがって、答えは(2)と求まります。 |
出典元
平成２１年度第三種電気主任技術者試験 理論科目B問題問１７
参考書
本ブログの管理人は、電験３種過去問マスタを使って電験３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント