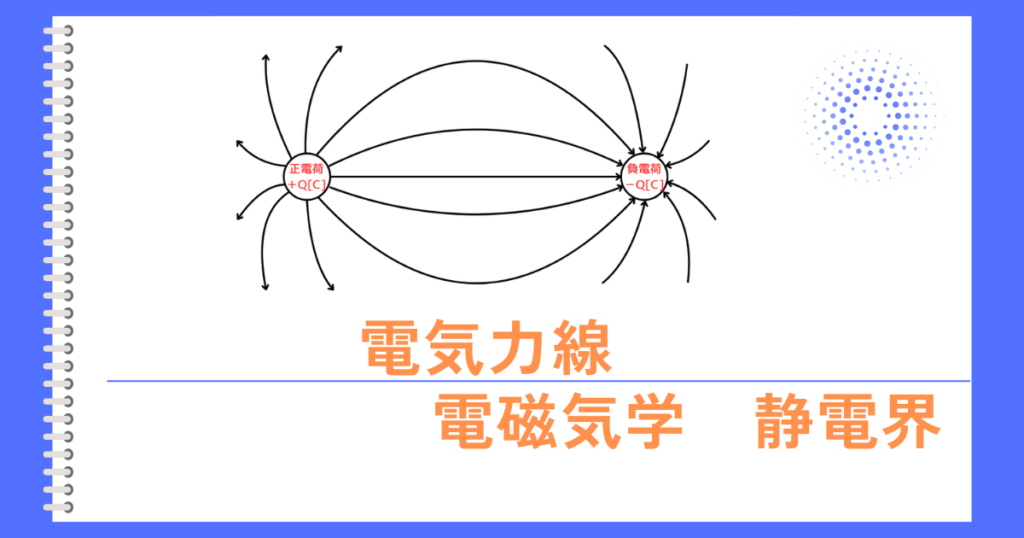
電位とは
電位とポテンシャルエネルギー
電位の意味
電界中で、単位電荷が持つ静電気力による位置エネルギー(ポテンシャルエネルギー)です。
単位電荷とは、\(q=1[C]\)の電荷のことです。
電位\(V[V]\)とポテンシャルエネルギー\(W[J]\)の関係
上記の電位の意味から、電位とポテンシャルエネルギーの関係を式にすると、
\(W=qV\)です。
電位\(V\)の単位は、実用的には\([V]\)を使用しますが、上式から
\([V]=[J/C]\)です。
重力による位置エネルギー・静電気力による位置エネルギー・電位を比較
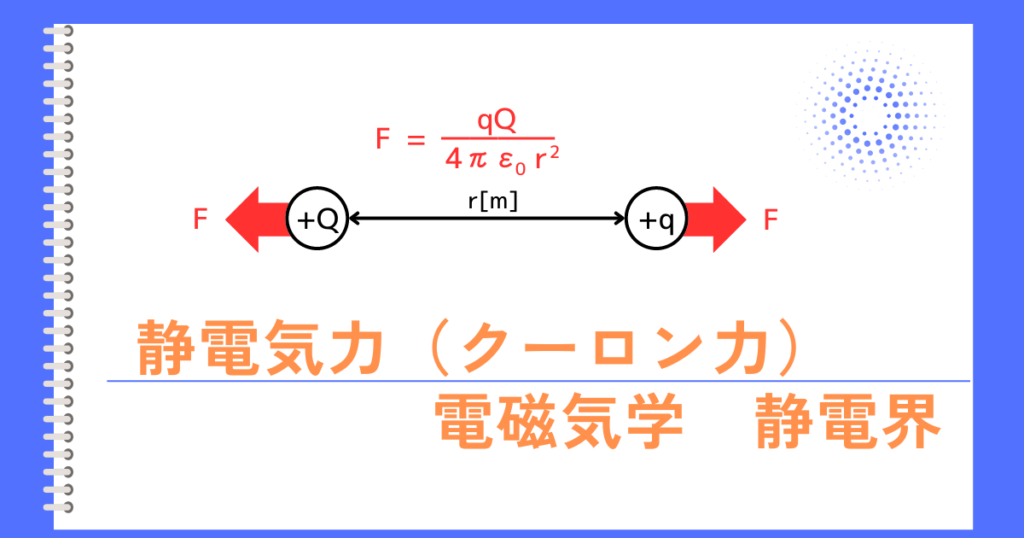
静電気力\(F[N]\)に逆らって電荷を移動させたときのエネルギーは、ポテンシャルエネルギーと呼びます。ポテンシャルエネルギーは、日本語にすると位置エネルギーです。
位置エネルギーというと、高校力学で学ぶ重力に逆らって物を持ち上げたときに、物に蓄えられる位置エネルギーが浮かぶと思います。
静電気力の位置エネルギー(ポテンシャルエネルギー)を、重力による位置エネルギーと比較すると同じような存在であることがわかります。
比較するために、重力・静電気力の位置エネルギーと電位を並べたイメージは次のようになります。なお、図の電界は、コンデンサの電界のように、位置によって変動しない一様な電界とします。
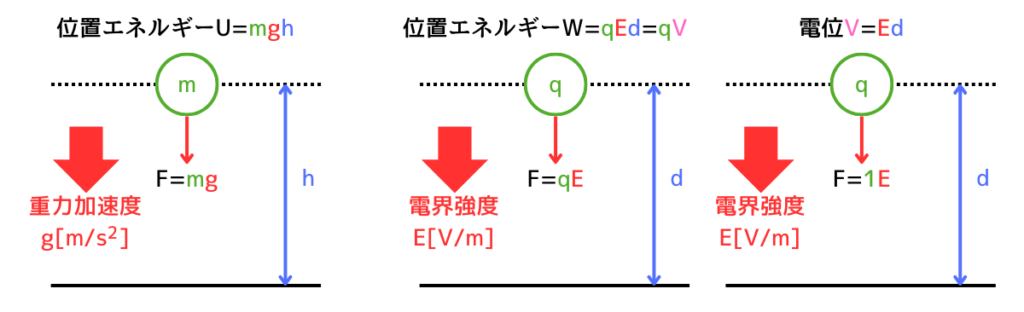
上図を比較すると、次のように対応していることがわかります。
・質量\(m[kg]\) ⇔ 電荷量\(q[C]\)
・重力加速度\(g[m/s^2]\) ⇔ 電界強度\(E[V/m]\)
・高さ\(h[m]\) ⇔ 距離\(d[m]\)
電位と電界
電位と電界の関係式
\(V=-\int_{基点}^{対象点}E dr\) ⇔ \(\displaystyle E=-\frac{dV}{dr}\)
電界\(E\)は、電位\(V\)を距離\(r\)で微分した形で表されます。そのことから、電界は電位の傾きであることがわかります。
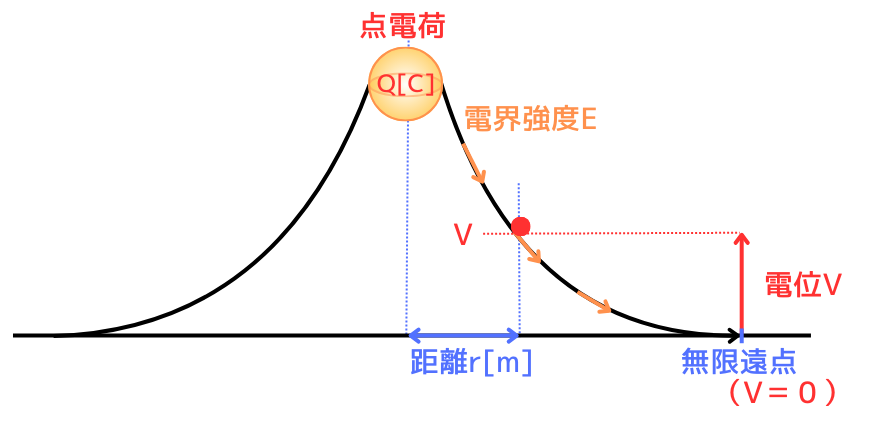
電位と電界の関係式は、単位電荷\(q=1[C]\)を、電界\(E[V/m]\)によって生じる静電気力\(F=qE=E[N]\)に逆らって、「基点」から「対象点」まで移動させた時の仕事が位置エネルギーとして蓄えられたことを表します。
※基点が定義されていないとき、つまり、単純に電位\(V[V]\)を求めるようなときは、
無限遠点:\(\infty\) を基点とします。
電界の式は、主に3パターンの式があります。
そのため、電界の式を積分して導出される電位の式も3パターン存在しますので、それぞれについて示していきます。
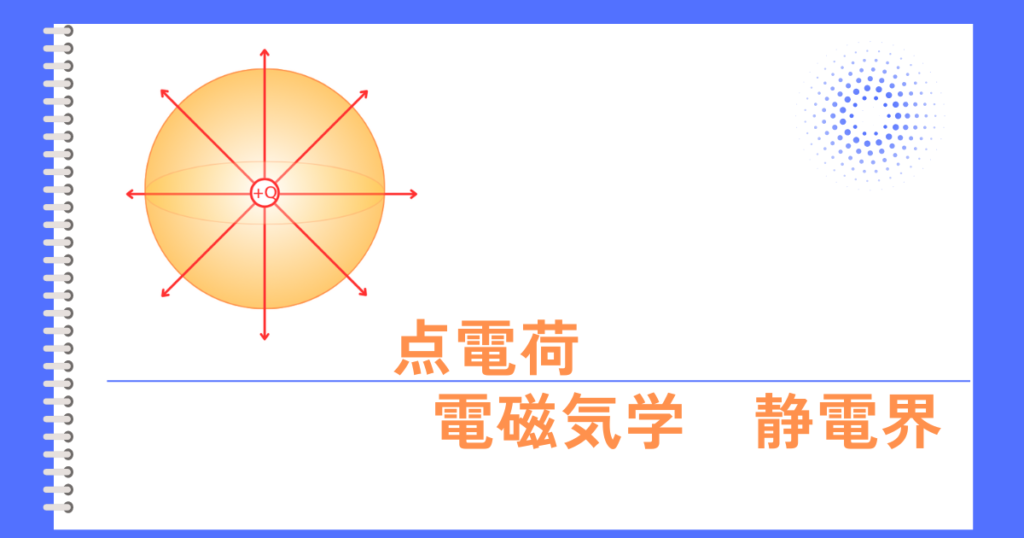
①点電荷が作る電界(距離の二乗\(r^2\)に反比例する電界)
②線電荷が作る電界(距離\(r\)に反比例する電界)
③コンデンサが作る電界(一様な電界)
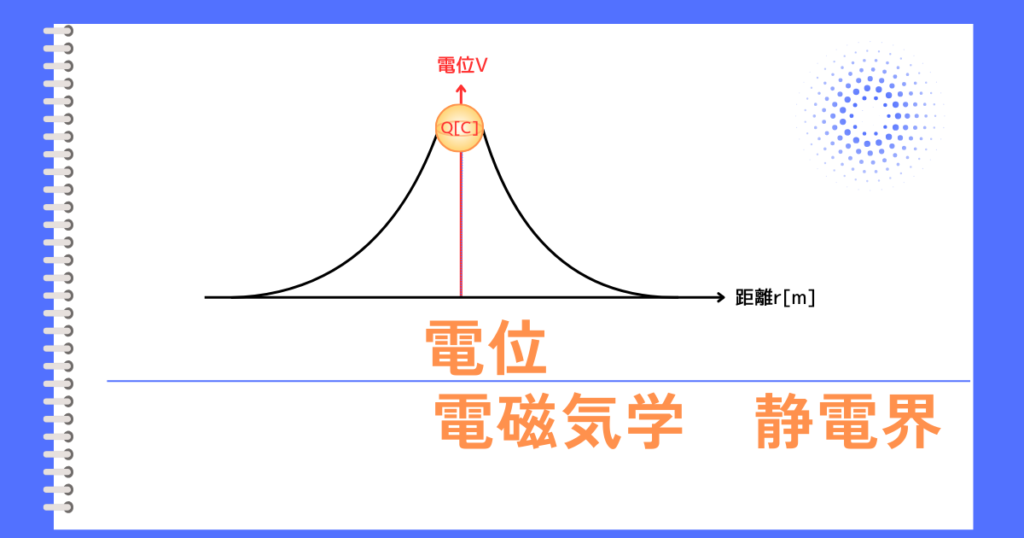
点電荷の電位
点電荷\(Q[C]\)が作り出す電界中の電位は、次式で表すことができます。
\(\displaystyle V=\frac{Q}{4πε_0r}\)
電位の式について導出します。
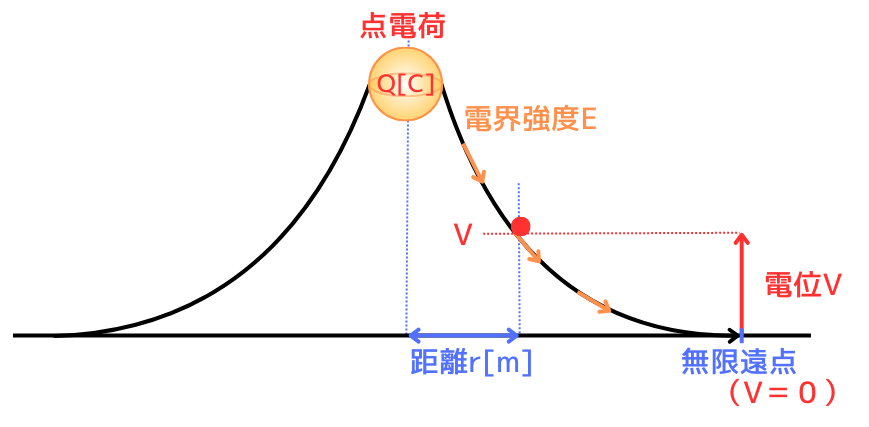
点電荷の作る電界の電界強度\(E[V/m]\)は、ガウスの法則から、
\(\displaystyle E=\frac{Q}{4πε_0r^2}[V/m]\) …①
この電界中で、単位電荷\(1[C]\)を基点から対象点まで移動させたときの電位を求めます。
このとき、
・基 点:無限遠点(∞)
・対象点:距離\(r[m]\)
とします。
電位\(V[V]\)と電界\(E[V/m]\)の関係式に①式を代入すると、
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{∞}^{r}\frac{Q}{4πε_0r^2} dr = \frac{Q}{4πε_0}\left[ \frac{1}{r} \right]_∞^r \\
&=& \frac{Q}{4πε_0}\left( \frac{1}{r}-\frac{1}{∞}\right) = \frac{Q}{4πε_0r}
\end{eqnarray}\)
以上、\(\displaystyle V=\frac{Q}{4πε_0r}\)が導出できました。
補足:電位差の導出
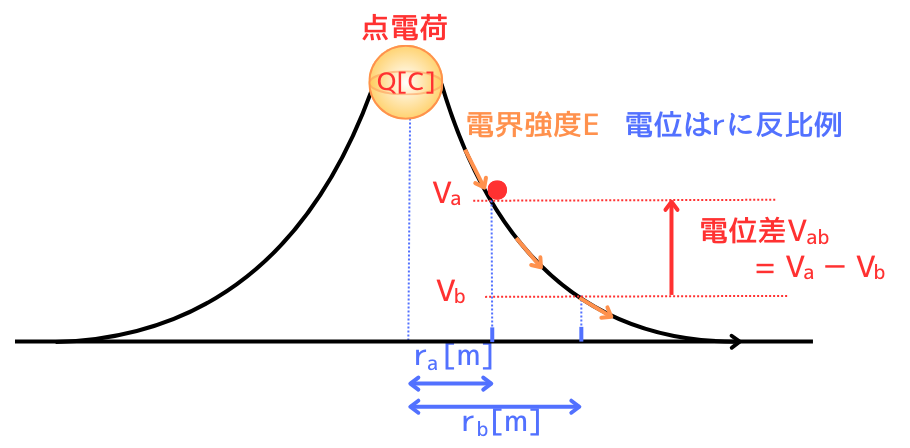
基点を無限遠点とせず、
・基 点:\(r_b[m]\)のとき、\(V_b[V]\)
・対象点:\(r_a[m]\)のとき、\(V_a[V]\)
とした場合、電位差\(V_{ab}=V_a-V_b\)になることついて導出します。
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{r_b}^{r_a} \frac{Q}{4πε_0r^2} dr = \frac{Q}{4πε_0}\left[ \frac{1}{r} \right]_{r_b}^{r_a} \\
&=& \frac{Q}{4πε_0}\left( \frac{1}{r_a}-\frac{1}{r_b}\right) = \frac{Q}{4πε_0r_a}-\frac{Q}{4πε_0r_b} = V_a-V_b
\end{eqnarray}\)
以上より、電位差\(V_{ab}=V_a-V_b\)が導出できました。
線電荷(同軸円導体)の電位
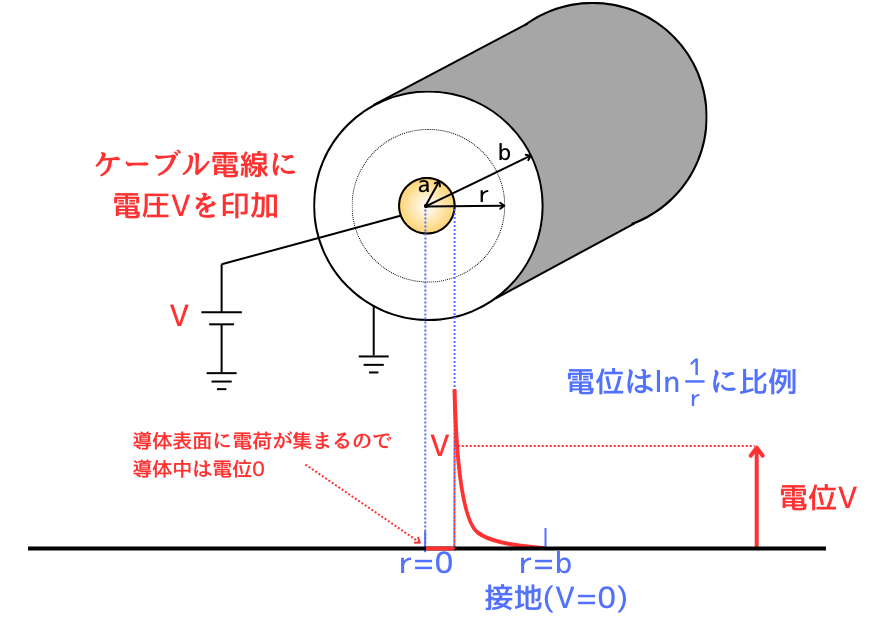
ケーブルのような1m当たりの線電荷\(q[C/m]\)が作り出す電位は、次式で表すことができます。
\(\displaystyle V=\frac{Q}{2πε_0}ln\frac{b}{r}\)
※1:bは、外部円筒導体の半径の長さであり、固定値です。
※2:b、rの長さは、共に内部導体の中心点からの長さとします。
※3:内部導体表面に電荷が集まるため、内部導体の電位は、\(V=0[V]\)です。
電験では、同軸円導体の電位分布を求める問題は少ないです。
しかし、同軸円導体の式(\(V=\frac{Q}{2πε_0}ln\frac{b}{r}\))から、\(Q=CV\)の関係を使用して、静電容量を求めるような問題は時々出題されます。
電位の式について導出します。
線電荷の作る電界の電界強度\(E[V/m]\)は、ガウスの法則から、
\(\displaystyle E=\frac{q}{2πε_0r}[V/m]\) …②
この電界中で、単位電荷\(1[C]\)を基点から対象点まで移動させたときの電位を求めます。
このとき、
・基 点:\(b[m]\)(外部円筒導体の半径)
・対象点:距離\(r[m]\)
とします。
※同軸円筒導体の場合、基点を無限遠点に取ると、計算が出来ないため、外部円筒導体の半径と定めています。
電位\(V[V]\)と電界\(E[V/m]\)の関係式に②式を代入すると、
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{b}^{r}\frac{q}{2πε_0r} dr = \frac{q}{2πε_0}\left[ ln r \right]_r^b \\
&=& \frac{q}{2πε_0}(ln b-ln r) = \frac{q}{2πε_0}ln \frac{b}{r}
\end{eqnarray}\)
以上、\(\displaystyle V=\frac{q}{2πε_0}ln \frac{b}{r}\)が導出できました。
コンデンサの電位
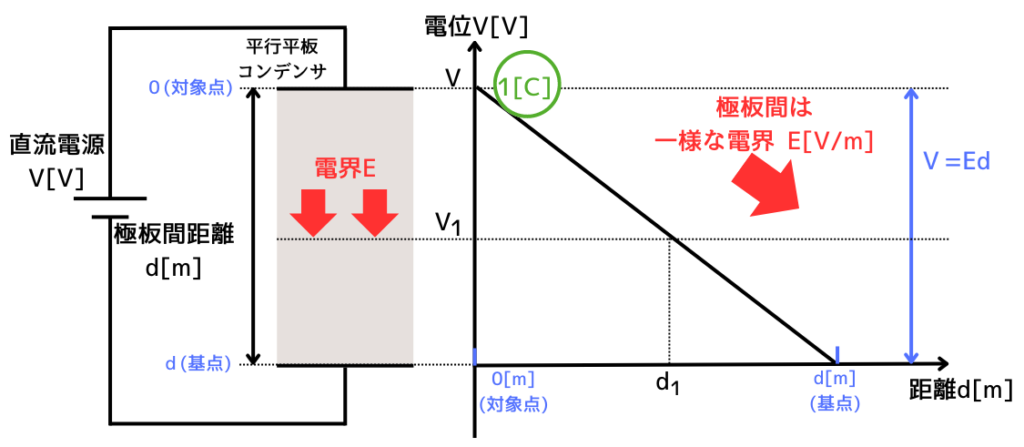
平行平板コンデンサの一様な電界\(E[V/m]\)の場における電位\(V[V]\)は、極板間距離\(d[m]\)を使用し、次式で表されます。
\(V=Ed\)
電位の式について導出します。
線電荷の作る電界の電界強度\(E[V/m]\)は、ガウスの法則から、
\(\displaystyle E=\frac{Q}{ε_0S}[V/m]\) …③
※Sは極板面積です。
この電界中で、単位電荷\(1[C]\)を基点から対象点まで移動させたときの電位を求めます。
このとき、コンデンサの極板間距離\(d[m]\)なので、
・基 点:\(d[m]\)
・対象点:\(0[m]\)
とします。
電位\(V[V]\)と電界\(E[V/m]\)の関係式に②式を代入すると、
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{d}^{0}\frac{q}{ε_0S} dr = \frac{q}{ε_0S}\left[ r \right]_0^d \\
&=& \frac{q}{ε_0S}(d-0) = \frac{q}{ε_0S}d=Ed
\end{eqnarray}\)
以上、\(\displaystyle V=Ed\)が導出できました。
電位と等電位面
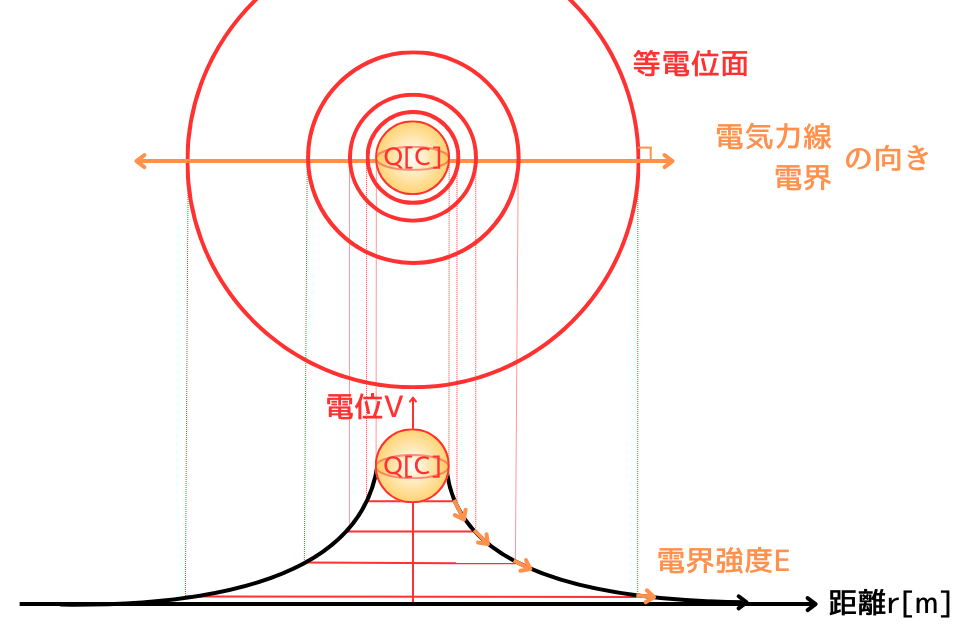
等電位面とは、電界中の電位の等しいところを繋げていくと出来る面を等電位面と呼びます。
等電位面には次の性質があります。
①等電位面は、電気力線や、電界の向きと直交します。
②等電位面上で電荷を動かす仕事は0です。
③等電位面の間隔が狭い程電界が強い。
④電位の異なる等電位面は交わりません。
⑤導体表面は等電位面となります。
過去問
難易度 ★☆☆☆☆
電験三種 令和5年度前期 問2 等電位面を含む論説
難易度 ★★☆☆☆
電験三種 令和4年度下期 問2 コンデンサと導体球の電位の論説
電験三種 令和元年度 問1 電位差の計算
電験三種 平成21年度 問17 コンデンサの電界・電位の計算
難易度 ★★★☆☆
電験三種 令和2年度下期 問1 電位と静電エネルギーの計算
関連記事(静電界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント