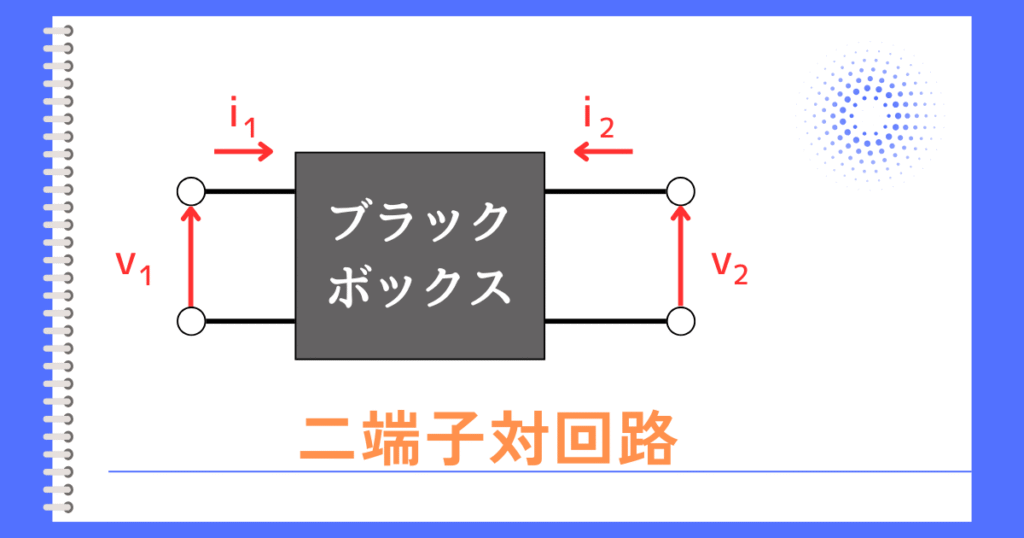
二端子対回路とは
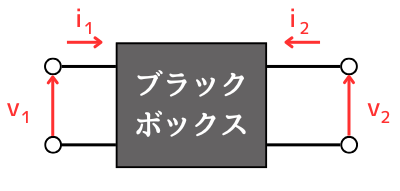
入力と出力の電流電圧の関係さえ分かれば、その回路の特性が分かるので、中身を考える必要がありません。
そのため、中身はわからないブラックボックスとすることで、回路を簡単なモデル化して簡単に解析できるようにした等価回路表現です。
二端子対回路の表現方法
二端子対回路の入出力は、\(v_{in}\)、\(i_{in}\)、\(v_{out}\)\(i_{out}\)の4つがあります。
この4つの関係を表す表現方法として、3つの方法があります。
Zパラメータ
\(\begin{bmatrix}v_1 \\ v_2 \end{bmatrix}=\begin{bmatrix}z_{11} && z_{12} \\z_{21} && z_{22} \end{bmatrix}\begin{bmatrix}i_1 \\ i_2 \end{bmatrix}\)
入出力の電流\(i_1,i_2\)により、入出力の電圧\(v_1,v_2\)を表す方法です。
この場合の係数はインピーダンス\(Z\)であるため、この係数行列をZパラメータと呼びます。
ブラックボックスとした回路を直列接続するとき、行列計算で特性を計算できる利点があります。
Yパラメータ
\(\begin{bmatrix}i_1 \\ i_2 \end{bmatrix}=\begin{bmatrix}y_{11} && y_{12} \\y_{21} && y_{22} \end{bmatrix}\begin{bmatrix}v_1 \\ v_2 \end{bmatrix}\)
入出力の電圧\(v_1,v_2\)により、入出力の電流\(i_1,i_2\)を表す方法です。
この場合の係数はアドミタンス\(Y\)であるため、この係数行列をYパラメータと呼びます。
ブラックボックスとした回路を並列接続するとき、行列計算で特性を計算できる利点があります。
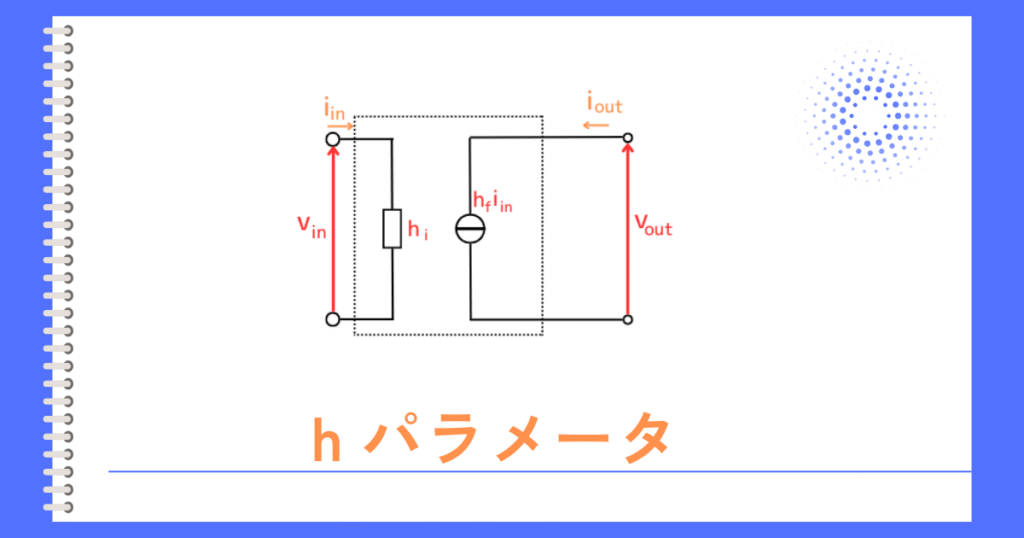
Hパラメータ
\(\begin{bmatrix}v_1 \\ i_2 \end{bmatrix}=\begin{bmatrix}h_{11} && h_{12} \\h_{21} && h_{22} \end{bmatrix}\begin{bmatrix}i_1 \\ v_2 \end{bmatrix}\)
入力電流\(i_1\)、出力電圧\(v_2\)により、
入力の電圧\(v_1\)、出力電流\(i_2\)を表す方法です。
この場合の係数はインピーダンス\(Z\)とアドミタンス\(Y\)が混ざっていることからハイブリッド(Hybrid)と呼ばれ、この係数行列をHパラメータと呼びます。
電子回路の解析では、主にHパラメータを使います。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント