過渡解析の概要
コイル、コンデンサがある回路では、スイッチを入り切りして電源ON/OFFすると電圧・電流の大きさが徐々に変化するようになります。
変化し続けている状態を過渡状態。
変化が終わり、電圧・電流が変化しなくなった状態を定常状態と呼びます。
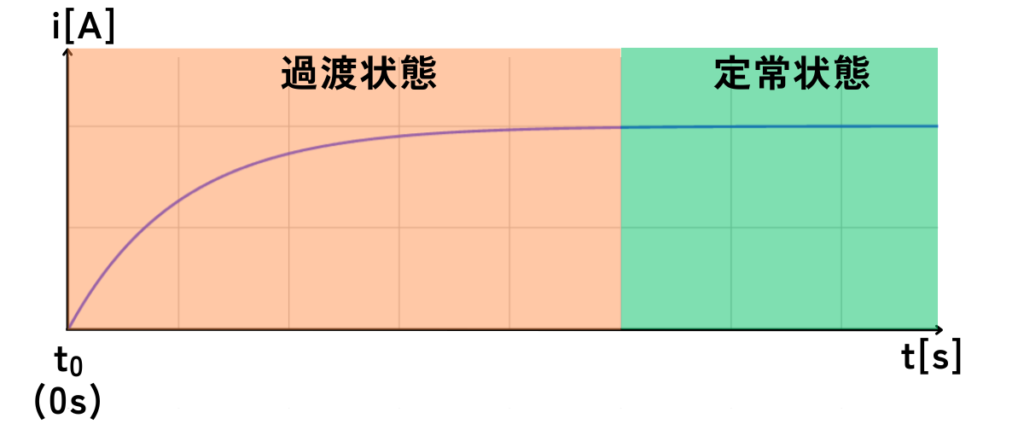
この過渡状態、定常状態を解析して、変化の様子を示すことを過渡解析と呼びます。
過渡解析の解法
過渡現象の解法は次の(1)~(3)の3つあります。本ページでは(1)について解説します。
(1)微分方程式を解く
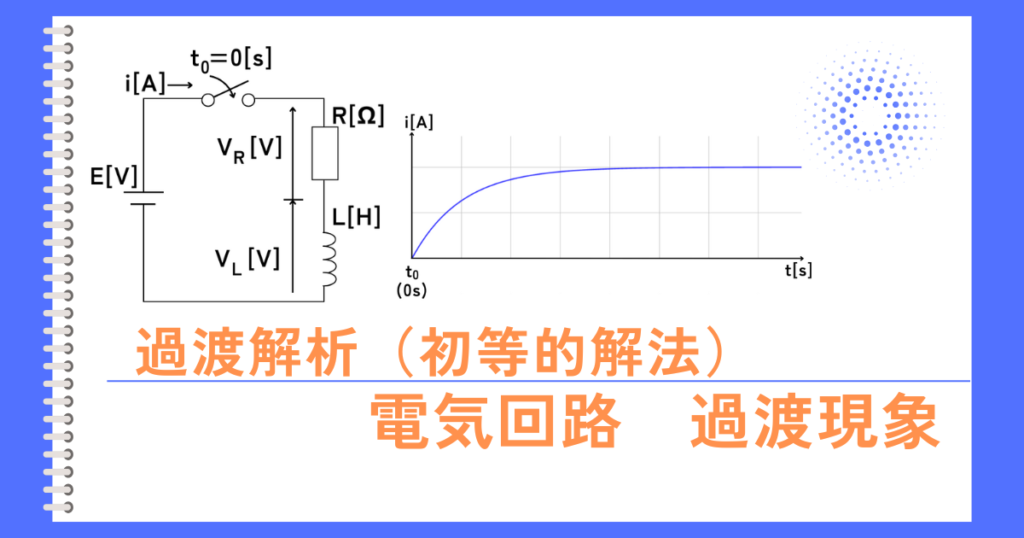
(2)初等的解法で解く(過渡解と定常解をそれぞれ解析後、重ねの理を使って足し合わせる)
(3)ラプラス変換
(1)の微分方程式を解く方法は、微分積分計算した後、積分定数を求めていく方法です。
過渡応答の考え方の基礎であるため理解をしておいた方が良いですが、非常に計算が煩雑なため、電験の試験中にこの解法で解くことはお勧めしません。
(2)3つの中で、一番早く、簡単に解ける解法です。
この解法を完全に理解しておけば、電験三種の過渡解析の問題はほぼ確実に点数が取れるようになります。
(3)大規模なシステムの応答や、安定性を求めるときに重要な解法です。
ラプラス変換すると、解析が難解な微分方程式を代数方程式として解けるメリットがあります。
しかし、①ラプラス変換 ⇒ ②代数方程式で回路解析 ⇒ ③逆ラプラス変換 の3つの工程が必要なため回答に時間が掛かるデメリットがあります。
ラプラス変換の公式を覚えなければならないため、電験三種の受験においては学ぶ必要はないです。
大規模なシステム解析をする際には必須であるため、電験二種の二次試験を受験するまでには完全な理解が求められます。
過渡解析(微分方程式)の手順
微分方程式を直接解く方法の手順について示します。
① 回路の微分方程式を立式
② 微小変化量(diとdt)を両辺に来るように式を整える
③ 両辺積分する
④ 積分定数\(C\)を求める
RL直列回路の過渡解析
微分方程式を直接解く過渡解析の実例として、RL直列回路の過渡解析を行います。
回路の微分方程式を立式
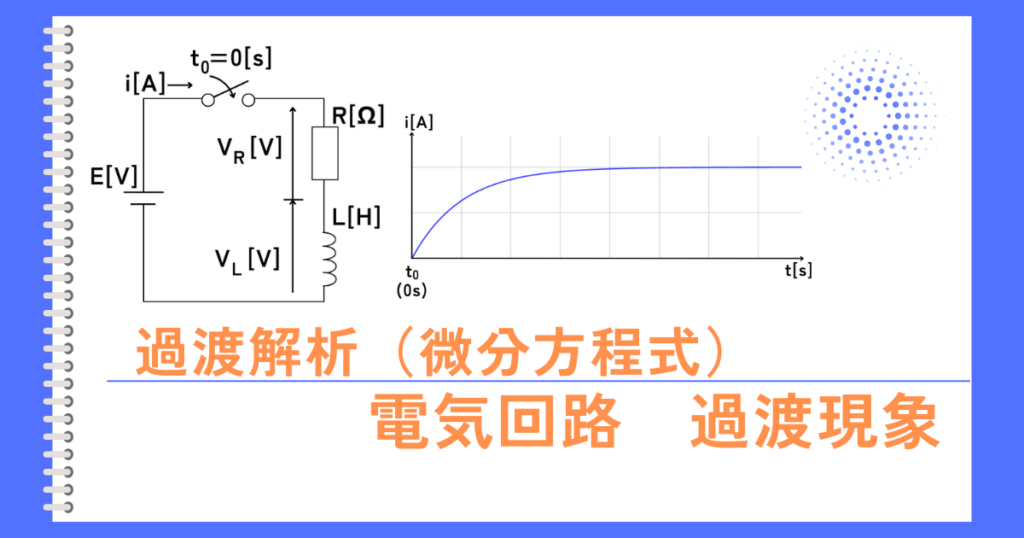
\(t_0=0\)秒以前はスイッチが開かれていて、\(t_0=0\)秒のタイミングでスイッチを投入するような、RL直列回路の過渡解析を例に考えます。
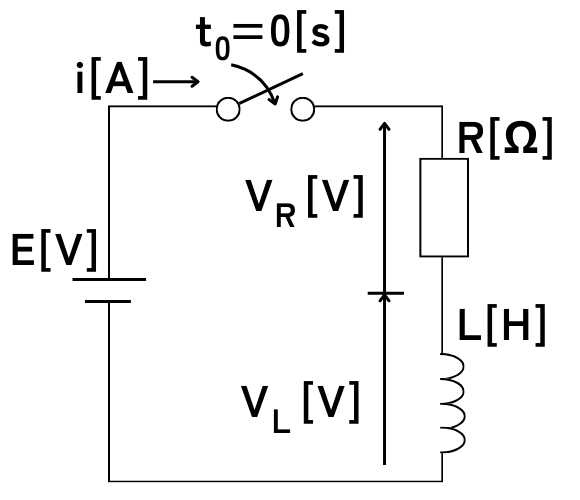
左図の回路は、キルヒホッフの電圧則から
\(E=V_R+V_L\) …(1)
です。
回路に流れる電流を\(i[A]\)としたとき、抵抗R、コイルLの両端に発生する電圧は次式で表されます。
\(V_R=Ri\) …(2)
\(V_L=L\frac{di}{dt}\) …(3)
(1)式に(2)・(3)式を代入すると、次のような微分方程式になります。
\(E=Ri+L\frac{di}{dt}\) …(4)
微小変化量(diとdt)を両辺に来るように式を整える
(4)式を整理していく。
\(\displaystyle E=Ri+L\frac{di}{dt}\) …(4)
⇔\(\displaystyle L\frac{di}{dt}=E-Ri\)
⇔\(\displaystyle \frac{1}{E-Ri}di=\frac{1}{L}dt\)
⇔\(\displaystyle \frac{1}{Ri-E}di=-\frac{1}{L}dt\) …(5)
両辺積分する
(5)式の両辺を積分していきます。
\(\displaystyle \frac{1}{Ri-E}di=-\frac{1}{L}dt\) …(5)
⇔\(\displaystyle \int \frac{1}{Ri-E}di=-\int \frac{1}{L}dt\)
⇔\(\displaystyle \frac{1}{R}ln(Ri-E)=-\frac{1}{L}t+C_1\)
⇔\(\displaystyle ln(Ri-E)=-\frac{R}{L}t+RC_1\)
⇔\(\displaystyle Ri-E=e^{-\frac{R}{L}t+RC_1}=e^{RC_1}e^{-\frac{R}{L}t}\)
\(A=e^{RC_1}\)とすると、
⇔\(\displaystyle Ri-E=Ae^{-\frac{R}{L}t}\) …(6)
積分定数\(C_1\)を求める
初期条件\(t=0\)のとき、\(i=0\)です。(6)式に代入すると、
\(\displaystyle -E=Ae^{-\frac{R}{L}0}=Ae^0=A\)
以上より、
\(A=-E\) …(7)
となります。
(7)式を(6)式に代入すると、
\(\displaystyle Ri-E=-Ee^{-\frac{R}{L}t}\)
⇔\(\displaystyle Ri=E-Ee^{-\frac{R}{L}t}\)
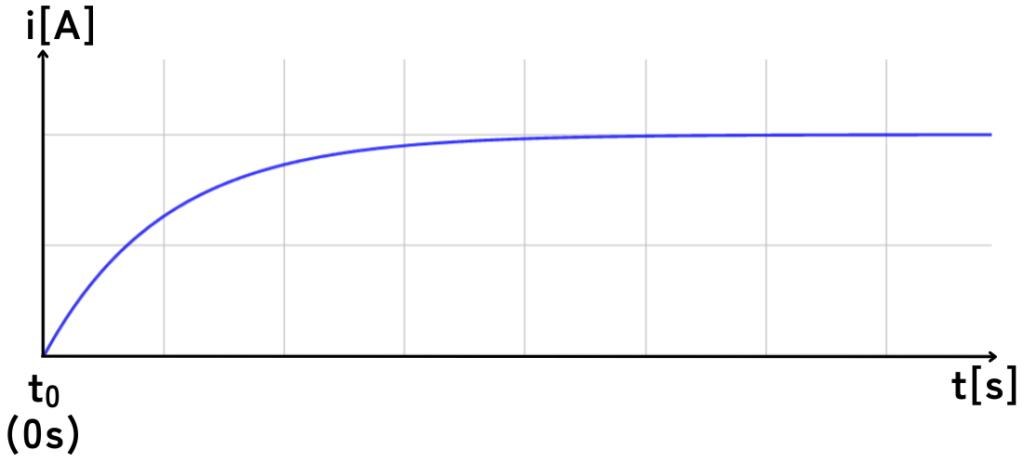
⇔\(\displaystyle i=\frac{E}{R}\left( 1-e^{-\frac{R}{L}t} \right)\)
この求まった式をグラフにすると、下図のようになります。
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント