概要
三相交流回路は、位相が120°ずつずれた3つの交流電源と、3つの負荷がYの形もしくは、Δの形に接続されて使われる回路です。
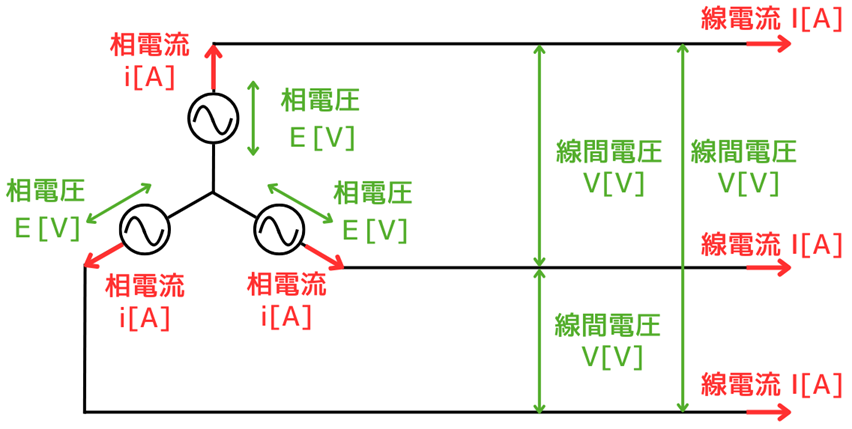
Y結線
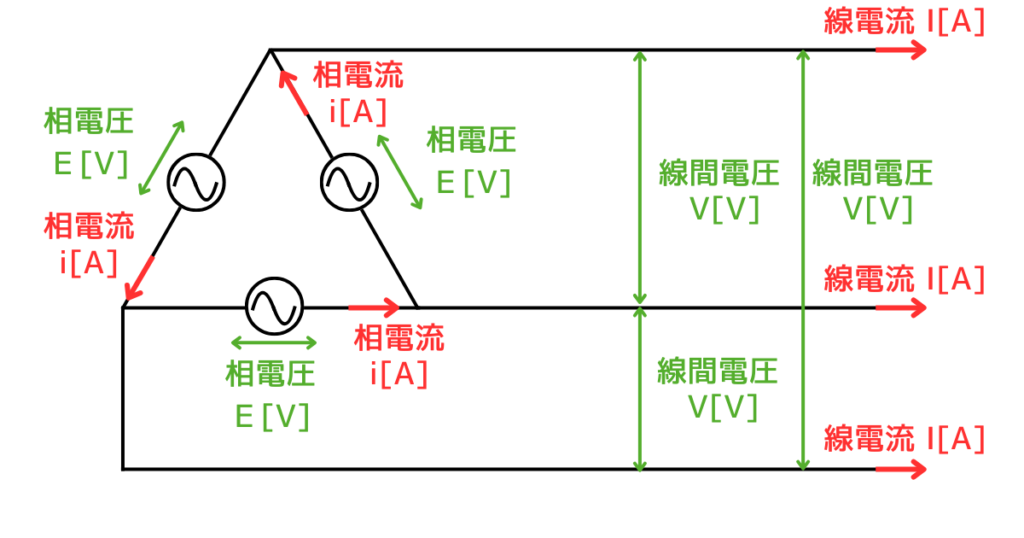
Δ結線
3つの交流電源のそれぞれの電圧は相電圧と呼び、交流電源を流れる電流は相電流と呼びます。
電源と負荷をつなぐ3本の電線のうち、2本の電線間の電圧を線間電圧と呼びます。3本の電線を流れる電流を線電流と呼びます。
三相交流では、単に電圧・電流と呼ぶときは、線間電圧と線電流を指します。
街中の電柱を通る配電線の電圧は、6600Vの高圧ですが、この6600Vも線間電圧です。
Y結線とΔ結線の電圧・電流の関係
相電圧\(E[V]\)と線間電圧\(V[V]\)、相電流\(i[A]\)と線電流\(I[A]\)の関係は、Y結線とΔ結線で異なります。
Δ結線・Y結線のそれぞれの電圧・電流の関係は次表の通りです。
| 電圧 | 電流 | |
| Y結線 | \(V=\sqrt{3}E\) \(V\)が\(E\)より30°進み | \(I=i\) |
| Δ結線 | \(V=E\) | \(I=\sqrt{3}i\) \(I\)が\(i\)より30°遅れ |
Y(スター)結線
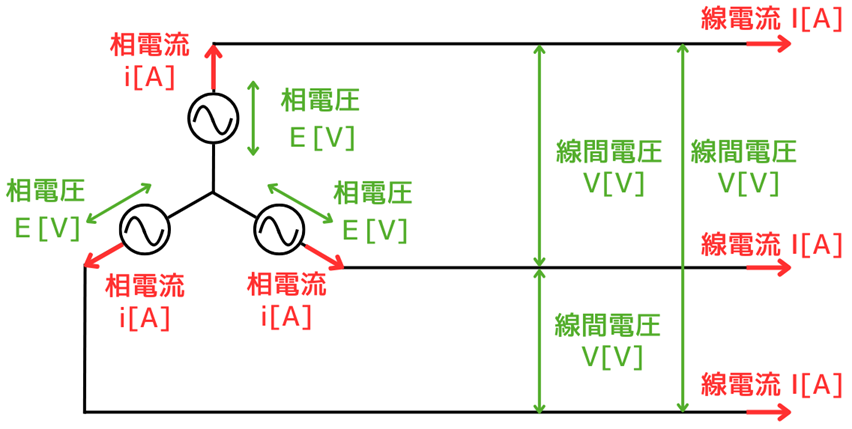
Y結線では、相電圧\(E[V]\)、線間電圧\(V[V]\)、相電流\(i[A]\)、線電流\(I[A]\)としたとき、次の通りの関係となります。
相電圧\(E[V]\)、線間電圧\(V[V]\)の関係
\(V=\sqrt{3}E\)
線間電圧は、相電圧よりも30°進み位相
相電流\(i[A]\)、線電流\(I[A]\)の関係
\(i=I\)
相電圧\(E[V]\)、線間電圧\(V[V]\)の関係の解析
線間電圧\(V\)が相電圧\(E\)の\(\sqrt{3}\)倍となり、位相が30°進む理由についてベクトル図を用いて解析します。
三相の線間電圧をまとめて示していくと情報量が多くてわずらわしいので、まずは\(V_{RS}\)だけ解析します。
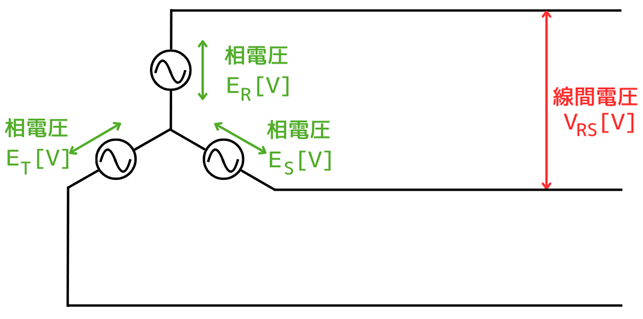
3相の各相をR相、S相、T相とし、各相の相電圧を、\(\dot{E}_R\)、\(\dot{E}_S\)、\(\dot{E}_T\)とします。
R相とS相の線間電圧を\(\dot{V}_{TR}\)とします。
120°ずつ位相がずれたRST各相の相電圧をベクトル図で表します。
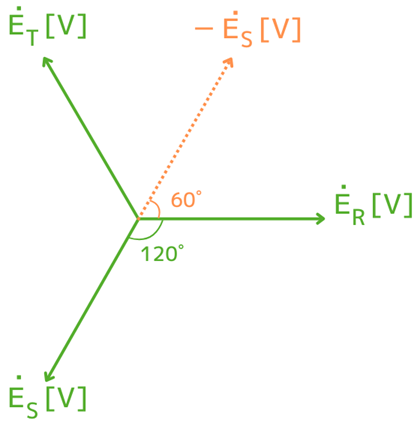
相電圧\(\dot{E}_R\)、\(\dot{E}_S\)、\(\dot{E}_T\)は、120°ずつずれた電圧です。
線間電圧\(\dot{V}_{RS}\)は、\(\dot{E}_R\)と\(\dot{E}_S\)の電位差なので、
\(\dot{V}_{RS}=\dot{E}_R-\dot{E}_S\)
です。
\(-\dot{E}_S\)は、\(\dot{E}_S\)の逆方向を向くベクトルなので、左図の橙色線で示すようなベクトルになります。
左図からわかる通り、\(\dot{E}_R\)と\(-\dot{E}_S\)の位相は60°ずれています。
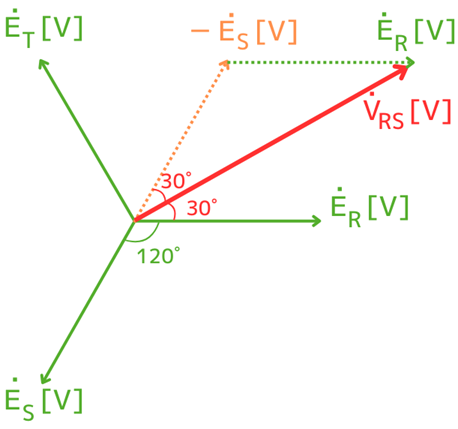
\(-\dot{E}_S\)のベクトルと、\(\dot{E}_R\)のベクトルを合成すると、\(\dot{V}_{RS}\)となるので、左図のようになります。
\(\dot{V}_{RS}\)が\(-\dot{E}_S\)、\(\dot{E}_R\)と作る角度は、60°を2分割するので30°になります。
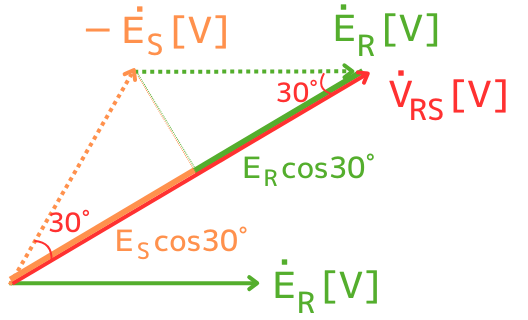
\(-\dot{E}_S\)から\(\dot{V}_{RS}\)に垂線を引くと、左図のようになります。
\(\dot{V}_{RS}\)の大きさ\(V_{RS}\)は、
\(V_{RS}=E_S cos30°+E_R cos30°\)
であることがわかります。
\(E_S\)と\(E_R\)の大きさは同じなので、
\(E_R=E_S\)としてまとめると。
\(V_{RS}=2E_Rcos30°=\sqrt{3}E_R\)
以上のことから、
R相とS相の線間電圧\(\dot{V}_{RS}\)は、R相の相電圧\(\dot{E}_R\)の\(\sqrt{3}\)倍の大きさで、位相が30°進んでいることがわかりました。
他の線間電圧\(V_{ST}\)、\(V_{TR}\)においても、同様に導かれます。三相分をまとめてベクトル図に表すと次のようになります。
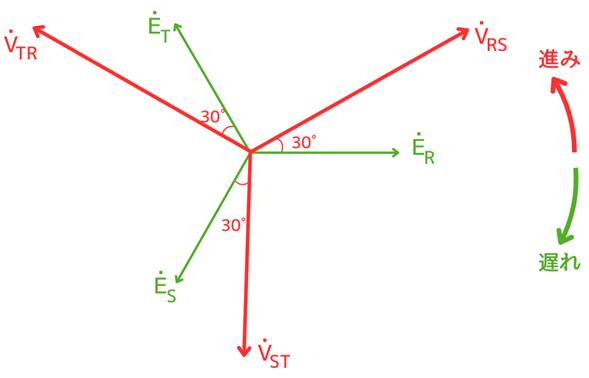
Δ(デルタ)結線
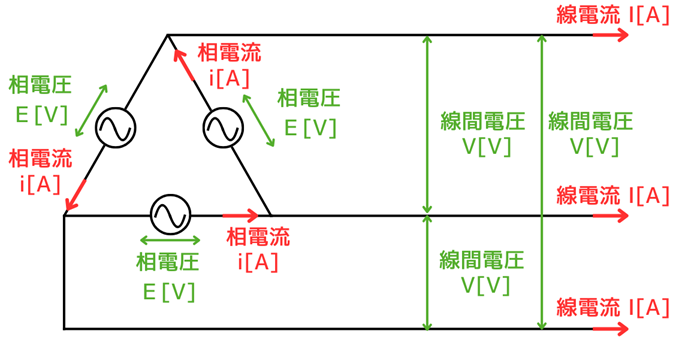
Δ結線では、相電圧\(E[V]\)、線間電圧\(V[V]\)、相電流\(i[A]\)、線電流\(I[A]\)としたとき、次の通りの関係となります。
相電圧\(E[V]\)、線間電圧\(V[V]\)の関係
\(V=E\)
相電流\(i[A]\)、線電流\(I[A]\)の関係
\(I=\sqrt{3}i\)
線電流\(I\)は、相電流\(i\)よりも30°遅れ位相
相電流\(i[A]\)、線電流\(I[A]\)の関係の解析
線電流\(I\)が相電流\(i\)の\(\sqrt{3}\)倍となり、位相が30°遅れる理由についてベクトル図を用いて解析します。
三相の線電流をまとめて示していくと情報量が多くてわずらわしいので、まずは\(I_{TR}\)だけ解析します。
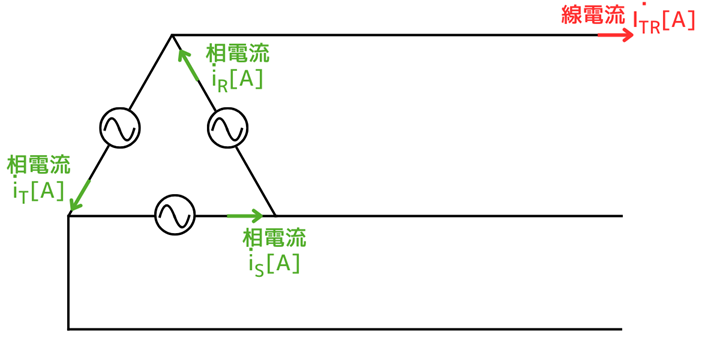
3相の各相をR相、S相、T相とし、各相の相電流を、\(\dot{i}_R\)、\(\dot{i}_S\)、\(\dot{i}_T\)とします。
R相とT相間の接続点から出る線電流を\(\dot{I}_{TR}\)とします。
120°ずつ位相がずれたRST各相の相電流をベクトル図で表します。
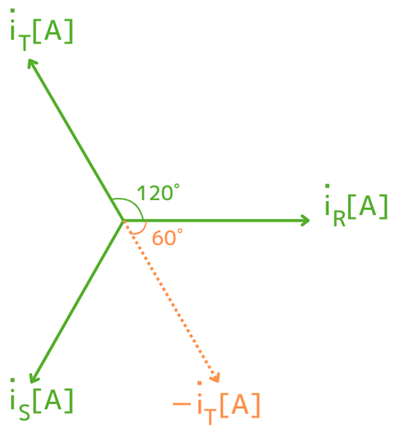
相電流\(\dot{i}_R\)、\(\dot{i}_S\)、\(\dot{i}_T\)は、120°ずつずれた電流です。
線電流\(\dot{I}_{TR}\)は、キルヒホッフの電流則から、
\(\dot{I}_{TR}=\dot{i}_R-\dot{i}_T\)
です。
\(-\dot{i}_T\)は、\(\dot{i}_T\)の逆方向を向くベクトルなので、左図の橙色線で示すようなベクトルになります。
左図からわかる通り、\(\dot{i}_R\)と\(-\dot{i}_T\)の位相は60°ずれています。
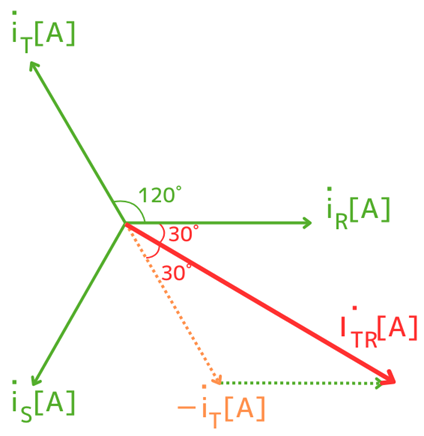
\(-\dot{i}_T\)のベクトルと、\(\dot{i}_R\)のベクトルを合成すると、\(\dot{I}_{TR}\)となるので、左図のようになります。
\(\dot{I}_{TR}\)が\(-\dot{i}_T\)、\(\dot{i}_R\)と作る角度は、60°を2分割するので30°になります。
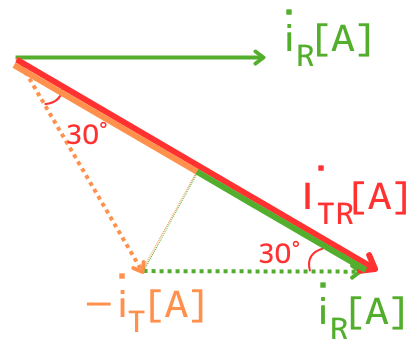
\(-\dot{i}_T\)から\(\dot{I}_{TR}\)に垂線を引くと、左図のようになります。
\(\dot{I}_{TR}\)の大きさ\(I_{TR}\)は、
\(I_{TR}=i_T cos30°+i_R cos30°\)
であることがわかります。
\(i_R\)と\(i_T\)の大きさは同じなので、
\(i_R=i_T\)としてまとめると。
\(I_{TR}=2i_Rcos30°=\sqrt{3}i_R\)
以上のことから、
R相とT相間の接続点から出る線電流\(\dot{I}_{TR}\)は、R相の相電流\(\dot{i}_R\)の\(\sqrt{3}\)倍の大きさで、位相が30°遅れていることがわかりました。
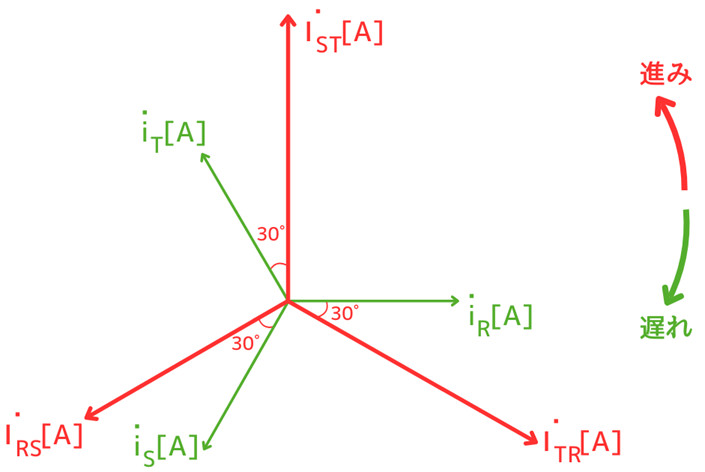
他の線電流\(I_{RS}\)、\(V_{ST}\)においても、同様に導かれます。三相分をまとめてベクトル図に表すと次のようになります。
関連記事(その他)
三相交流回路
交流回路
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント