テブナンの定理
回路理論を勉強する上で、初学者が初っ端に出くわすよくわからない定理の代表格でしょう。
その理由は、テブナンの定理の手順の説明は多いですが、その理屈をすっ飛ばしていることが多いためでしょう。その結果、説明の通りよくわからない操作をしたら、何となく回路解析が出来たみたいな出会いをすることが多くなります。
本ページでは、テブナンの定理の目的、テブナンの定理の使い方、テブナンの定理の証明の3点について説明していきます。
テブナンの定理の目的
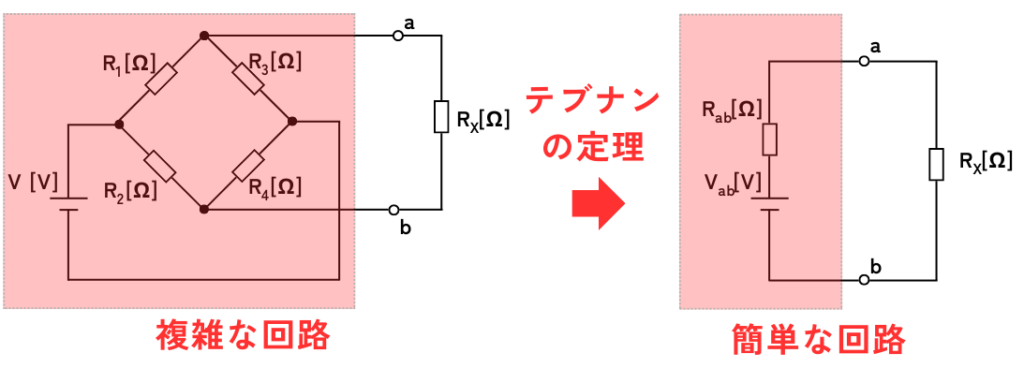
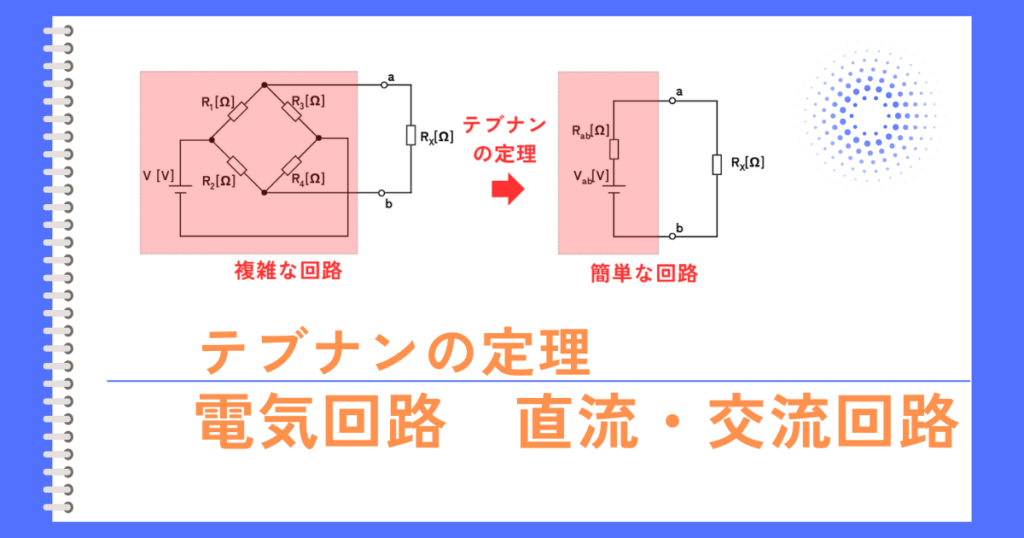
テブナンの定理を使う目的は、複雑な回路を簡単化して計算しやすくすることです。
図の様な複雑な回路があり、複雑な回路の端子abに接続した抵抗\(R_x\)に流れる電流や、\(R_x\)で消費される電力を解析したいと考えたとすると、計算量が非常に多くなります。
そこで、テブナンの定理を使うことで複雑な回路の中の電源・抵抗をまとめることが出来るため、簡単に回路解析が出来るようになります。
この定理は、直流回路だけでなく、交流回路でも使用することができるため、様々な回路解析において頻繁にお世話になるツールとなることでしょう。
テブナンの定理の使い方
テブナンの定理の使い方を、実例を交えながら解説します。
テブナンの定理を使って簡単化する回路部分を、薄い赤背景で囲っています。
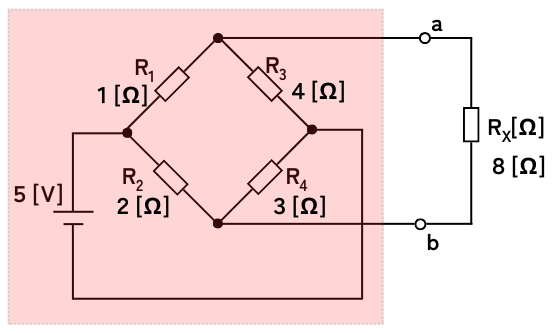
テブナンの定理の手順は次の4ステップで簡単な等価回路に書き換えられます。
① 端子a,bの右側の回路を切り離す
② 等価抵抗\(R_{ab}\)を求める
③ 等価電源\(V_{ab}\)を求める
④ 等価回路に書き換える
① 端子a,bの右側の回路を切り離す
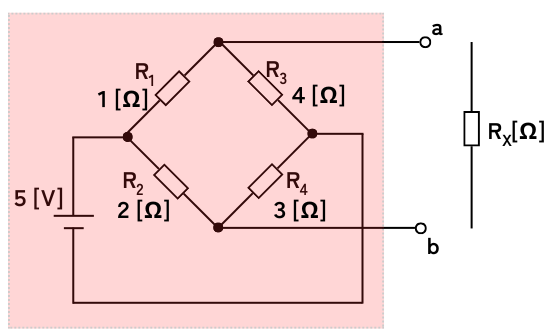
複雑な回路から解析したい部分である端子a,bの右側の回路を切り離します。
左図の回路図例の場合、\(R_x\)について解析をしたいため、端子a、bから切り離して開放します。
② 等価抵抗\(R_{ab}\)を求める
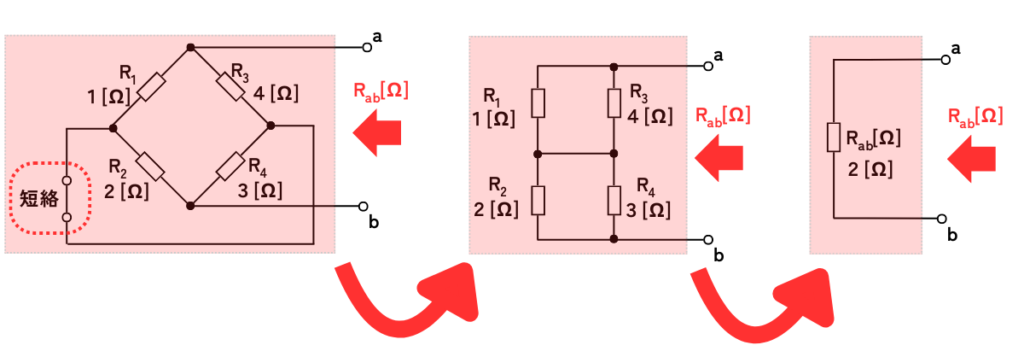
このステップでは、最初に回路中の電源を除去します。
・電圧源\(V\)は、短絡して回路から除去します。
・電流源\(I\)は、開放して回路から除去します。
次に、端子a、bから見た合成抵抗を求めます。
計算をしていくと、\(R_{ab}=2Ω\)となります。
③ 等価電源\(V_{ab}\)を求める
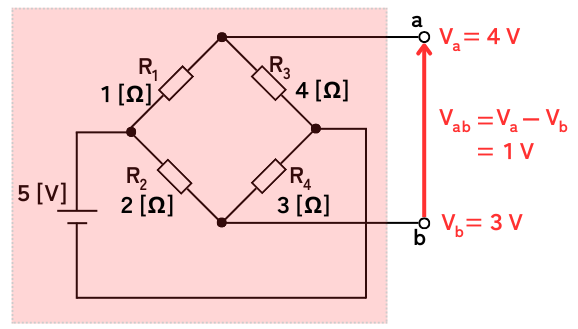
端子a、bの電位\(V_a\)、\(V_b\)を求めます。
\(V_a=\frac{R_3}{R_1+R_3}V=\frac{4}{5}・5=4V\)
\(V_b=\frac{R_4}{R_2+R_4}V=\frac{3}{5}・5=3V\)
次に、端子a、bの電位差\(V_{ab}\)を求めます。
\(V_{ab}=V_a-V_b=4-3=1V\)
④ 等価回路に書き換える
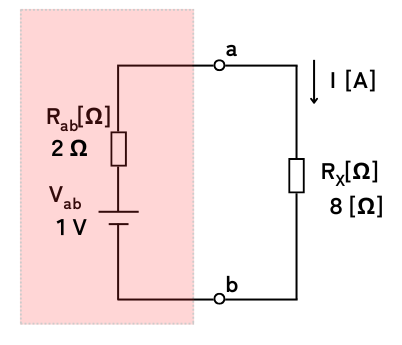
等価回路に書き換えたことで、\(R_x\)に流れる電流\(I_x\)、消費電力\(P_x\)は簡単に求めることができるようになります。
\(\displaystyle I_x=\frac{V_{ab}}{R_{ab}+R_x}=\frac{1}{2+8}=0.10A\)
\(P_x=I_x^2R_x=0.1^2・8=0.08W\)
テブナンの定理の証明

何故、テブナンの定理の使い方の項目の手順を踏むだけで、複雑な回路を簡単化できるかについて証明します。
テブナンの定理の証明
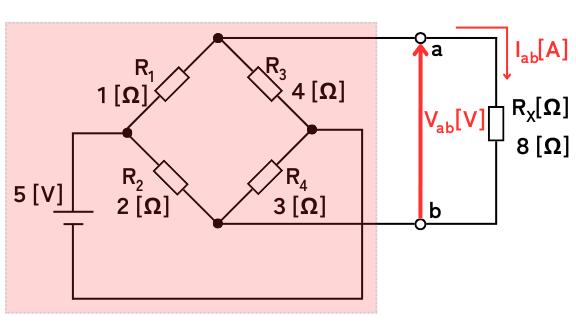
①簡単化をする前の複雑な回路
複雑な回路に端子a,bで接続された\(R_x[Ω]\)に流れている電流を\(I_{ab}[A]\)とします。
端子a,bの電位差を\(V_{ab}\)とします。
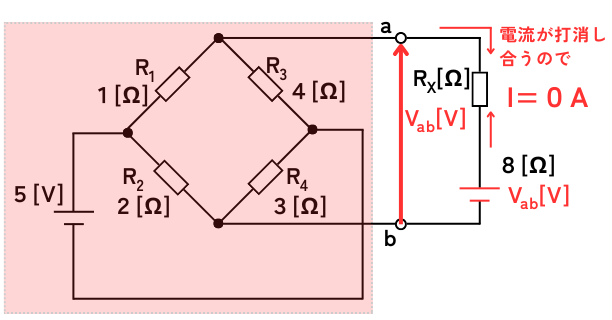
②電源\(V_{ab}\)を接続
\(R_x[Ω]\)に流れる電流が、\(I=0A\)となるように、電圧が調整された電圧源\(V_{ab}\)を接続します。
\(V_{ab}\)は、端子a,bの電位差と同じ電圧であり、この電圧が、テブナンの定理で簡単化した後の電圧\(V_{ab}\)となります。
③重ねの理で分解
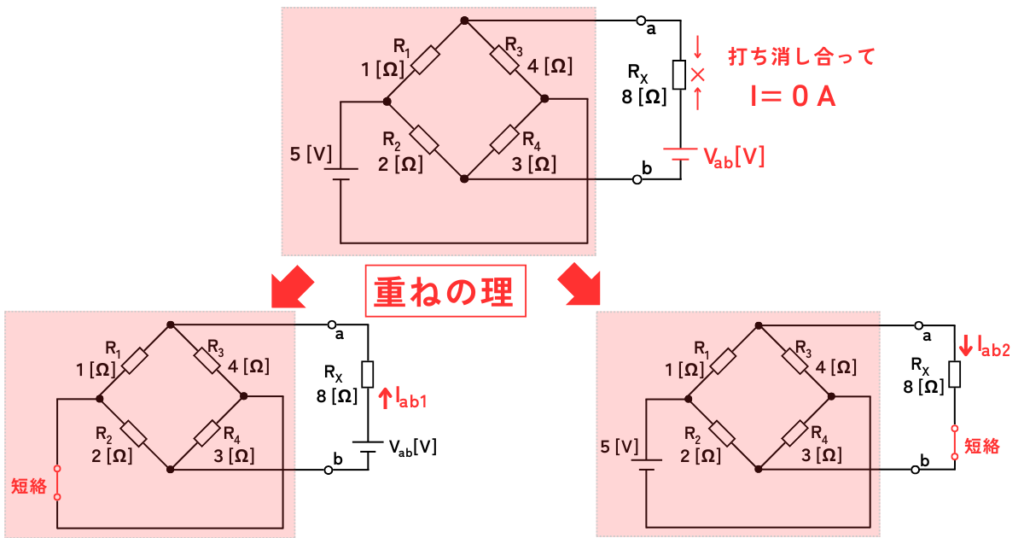
②の回路を、各電源毎に重ねの理で分解します。
分解すると、次の2つの回路に分けることが出来ます。
・\(V_{ab}\)が\(R_x\)に\(I_{ab1}\)を流す回路 ←重要
・\(5V\)の電源が\(R_x\)に\(I_{ab2}\)を流す回路
④複雑な回路を合成抵抗\(R_{ab}\)にまとめる
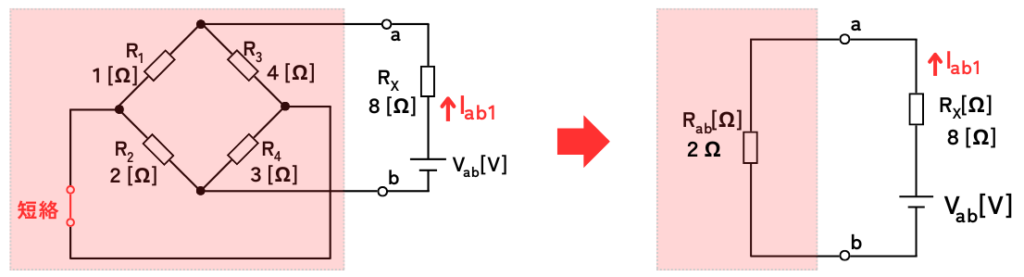
端子a,bより左側の、赤背景で囲われている複雑な回路の合成抵抗\(R_{ab}\)を求め、回路を合成抵抗に置き換えると、ほぼテブナンの定理で簡単化された回路になります。
⑤電源\(V_{ab}\)の位置と向きを替える
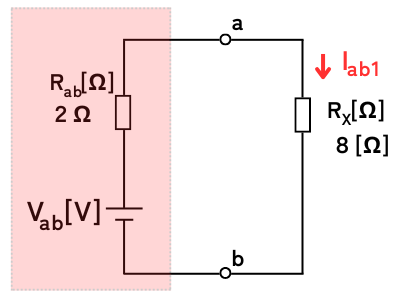
電源\(V_{ab}\)の位置と接続の向きを変えると、テブナンの定理で簡単化した回路の形となります。
まとめ
②電源\(V_{ab}\)を接続のステップでは、
端子a,b間の電位差に等しい等価電源\(V_{ab}\)を接続することで\(I=0A\)となることから、\(R_x\)の回路を切り離す操作がされたとみなすことが出来ます。
④複雑な回路を合成抵抗\(R_{ab}\)にまとめるのステップでは、
端子a,bから見た等価抵抗\(R_{ab}\)を求めたことと同じとなります。
以上より、テブナンの定理の使い方の項目の手順を踏むだけで、複雑な回路を簡単化できることがわかりました。
関連記事
直流回路
交流回路
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント